21.2.4 因式分解法 课件 (共28张PPT)
文档属性
| 名称 | 21.2.4 因式分解法 课件 (共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 13:53:06 | ||
图片预览







文档简介
(共28张PPT)
人教九上数学同步精品课件
人教版九年级上册
21.2.4 因式分解法
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.能用因式分解法解数字系数的一元二次方程.
2.会根据方程的特点选用合适的方法解一元二次方程.
学习目标
重点
难点
1、解下列一元二次方程:
新课引入
(1)x - 7 = 0
解:移项得,x = 7
即
∴
(2)x + 10x + 9 = 0
解:移项得,x + 10x = -9.
配方,得 x + 10x + 5 = 16
(x + 5) = 16
由此可得 x + 5 = ±4
(3)2x - 7x = 0
解:a=2,b= -7,c=0.
b2-4ac=49>0.
∴方程有两个不等的实数根
即
(3)(2x-5) =(x+7)
解:两边开平方得
2x-5=±(x+7)
所以 2x-5=x+7 或 2x-5=-x-7
即
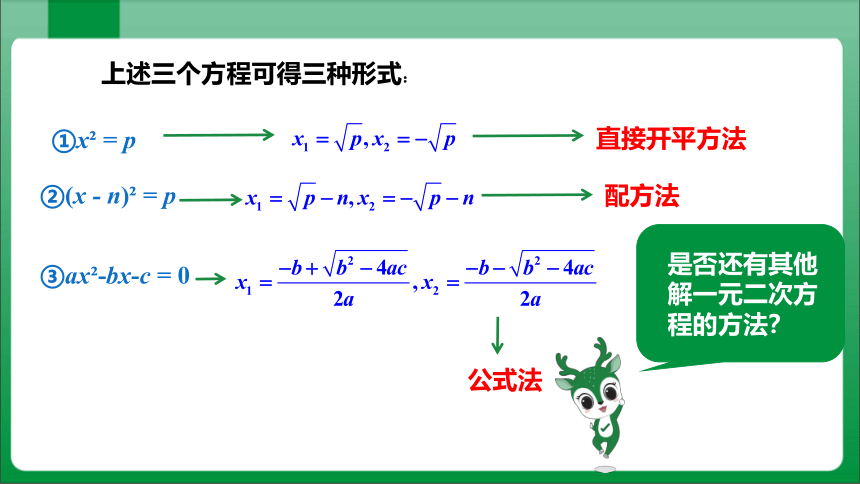
上述三个方程可得三种形式:
①x = p
②(x - n) = p
③ax -bx-c = 0
是否还有其他解一元二次方程的方法?
直接开平方法
配方法
公式法
问题 根据物理学规律,如果把一个物体从地面以10 m/s的速度竖直上抛,那么经过 x s物体离地
面的高度(单位:m)为10x-4.9x2.
你能根据上述规律求出物体经过多少秒落回地面吗(精确到0.01s)
分析:设物体经过 x s落回地面,这时它离地面的高度为0 m ,即
10x-4.9x2 =0 ①
一 因式分解法解一元二次方程
新知学习
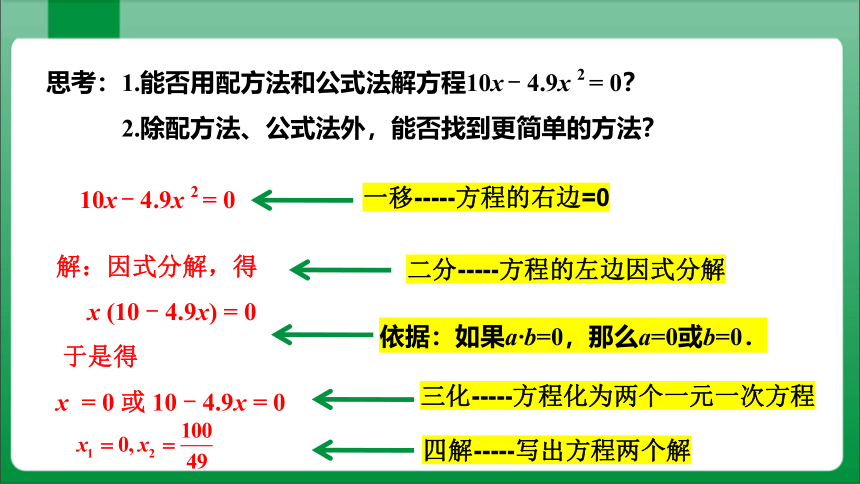
思考:1.能否用配方法和公式法解方程10x - 4.9x 2 = 0?
2.除配方法、公式法外,能否找到更简单的方法?
10x - 4.9x 2 = 0
解:因式分解,得
x (10 - 4.9x) = 0
于是得
x = 0 或 10 - 4.9x = 0
一移-----方程的右边=0
二分-----方程的左边因式分解
三化-----方程化为两个一元一次方程
四解-----写出方程两个解
依据:如果a·b=0,那么a=0或b=0.
这种通过因式分解,将一个一元二次方程转化为两个一元一次方程求解的方法叫做因式分解法.
因式分解法的概念
因式分解法的基本步骤
一移——方程的右边 = 0;
二分——方程的左边因式分解;
三化——方程化为两个一元一次方程;
四解——写出方程的两个解.
简记歌诀:
右化零 左分解
两因式 各求解
针对训练
1.解下列方程:
解:因式分解,得
于是得
x-2=0或x+1=0,
x1=2,x2=-1.
(x-2)(x+1)=0.
解:移项、合并同类项,得
因式分解,得
( 2x+1)( 2x-1 )=0.
于是得
2x+1=0或2x-1=0,
解:化为一般式为
x2-2x+1 = 0.
因式分解,得
(x-1)(x-1) = 0.
有 x - 1 = 0 或 x - 1 = 0,
x1=x2=1.
解:因式分解,得
有 x = 0 或 ,
例 选择合适的方法解方程:
(1)3x(2x+1)=4x+2
二 选择合适的方法解一元二次方程
因式分解最优
(2)(2x-3)2=(3x-2)2
因式分解法:
解:移项,得(2x-3)2-(3x-2)2 =0.
因式分解,得
[(2x-3)+(3x-2)][(2x-3)-(3x-2)]=0.
即(5x-5)(-x-1)=0,
∴5x-5=0,或-x-1=0,
∴x1=1,x2=-1.
直接开平方法:
解:两边直接开平方,得
2x-3=±(3x-2) ,
于是得
2x-3=3x-2 ,2x-3=-3x+2
∴x1=-1,x2=1.
(2)(2x-3)2=(3x-2)2
公式法:
解:方程化为x2-1=0.
a=1,b=0,c=-1.
b2-4ac=4>0.
方程有两个不等的实数根
即
(3) x2 - 12x = 4
配方法:
解: x2 - 12x + 62 = 4 + 62,
即 (x - 6)2 = 40.
开平方,得
解得 x1= ,
x2=
直接开平方最优
(3) x2 - 12x = 4
公式法:
解:方程化为x2 - 12x-4=0.
a=1,b=-12,c=-4.
b2-4ac=(-12) -4×1×(-4)=160>0.
方程有两个不等的实数根
即
(4) 3x2 = 4x + 1
公式法:
解:方程化为3x2 - 4x-1=0.
a=3,b=-4,c=-1.
b2-4ac=(-4) -4×3×(-1)=28>0.
方程有两个不等的实数根
即
配方法最优
(4) 3x2 = 4x + 1
配方法:
解:移项,系数化为1,得
即
如何选择最简单的方法,解一元二次方程?
公式法最优
方法 适用方程 适用特点
直接开平方法 ax2+c =0(m≠0,ac<0) (x+m) =n(n≥0) 一次项系数为0或左右两边能直接开平方
因式分解法 ax +bx+=0(a≠0) (mx+n)(dx+e)=0(m,d≠0) 方程求解过程中,等式两边不能同时约去含有相同未知数的因式
公式法 所有一元二次方程(b -4ac≥0) 把式子化成一般形式,方程的右边一定要化为0
配方法 x +px+q=0(p -4p≥0) 二次项系数化为1后,一次项系数是偶数的一元二次方程,且各项系数比较小,便于配方
归纳
思路:都是降次,将一元二次方程转化为一元一次方程解决
针对训练
1.将下列序号填到对应的横线上.
① x2-3x+1=0 ; ② 3x2-1=0 ; ③ -3t2+t=0 ; ④ x2-4x=2 ;
⑤ 2x2-x=0; ⑥ 5(m+2)2=8;⑦ 3y2-y-1=0; ⑧ 2x2+4x-1=0;
⑨ (x-2)2=2(x-2).
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
②
⑥
③
⑤
⑨
①
⑦
⑧
④
1. 请选择你认为适当的方法解下列方程.
(1)(x+4) =4x +1-4x (2)x -4x-1=0
直接开平方法:
解:整理,得
(x+4) =(2x-1)
x+4=±(2x-1)
x+4=2x-1或x+4=-2x+1
即
配方法:
解:
随堂练习
即
(3)2x +x-1=0 (4)x -3x=0
公式法:
解:a=2,b=1,c=-1.
b2-4ac=1 -4×2×(-1)=7>0.
方程有两个不等的实数根
即
所以x=0,或x-3=0
即
因式分解法:
解: x(x-3)=0
2.改错
(2x+3)(x-2)=(x-2)
解:2x+3 =1 ①
2x= -2 ②
x= -1 ③
上述过程从第______步开始出错,请你写出正确的解决过程.
①
改:
解:(2x+3)(x-2)=(x-2),
(2x+3)(x-2)-(x-2)=0,
(2x+2)(x-2)=0,
2x+2=0或 x-2=0
即
3. 把小圆形场地的半径增加5m得到大圆形场地,场地面积增加到原来的2倍,求小圆形场地的半径.
解:设小圆形场地的半径为r,
根据题意 ( r + 5 )2π=2r2π.
因式分解,得
于是得
答:小圆形场地的半径为
4.一个等腰三角形的底边长是 6,腰长是一元二次方程
x2-8x + 15=0 的一根,则此三角形的周长是___________
16
(x-3)(x-5)2=0
概念
步骤
简记歌诀:
右化零 左分解
两因式 各求解
如果a ·b=0,那么a=0或b=0.
原理
当右边=0时,将方程左边因式分解.
a(x+m)(x+n)=0
(mx+n)(dx+e)=0(m,d≠0)
因式分解法
课堂小结
直接开平方法
所有一元二次方程
(b -4ac≥0)
ax2+c =0(m≠0,ac<0)
(x+m) =n(n≥0)
一次项系数为0或左右两边能
直接开平方
一元二次
方程解法
因式分解法
ax +bx+=0(a≠0)
(mx+n)(dx+e)=0(m,d≠0)
方程求解过程中,等式两边
不能同时约去含有相同未知
数的因式
公式法
把式子化成一般形式,方
程的右边一定要化为0
配方法
x +px+q=0(p -4p≥0)
把二次项系数化为1后,
一次项系数是偶数的一元
二次方程,且各项系数比
较小,便于配方
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
21.2.4 因式分解法
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.能用因式分解法解数字系数的一元二次方程.
2.会根据方程的特点选用合适的方法解一元二次方程.
学习目标
重点
难点
1、解下列一元二次方程:
新课引入
(1)x - 7 = 0
解:移项得,x = 7
即
∴
(2)x + 10x + 9 = 0
解:移项得,x + 10x = -9.
配方,得 x + 10x + 5 = 16
(x + 5) = 16
由此可得 x + 5 = ±4
(3)2x - 7x = 0
解:a=2,b= -7,c=0.
b2-4ac=49>0.
∴方程有两个不等的实数根
即
(3)(2x-5) =(x+7)
解:两边开平方得
2x-5=±(x+7)
所以 2x-5=x+7 或 2x-5=-x-7
即
上述三个方程可得三种形式:
①x = p
②(x - n) = p
③ax -bx-c = 0
是否还有其他解一元二次方程的方法?
直接开平方法
配方法
公式法
问题 根据物理学规律,如果把一个物体从地面以10 m/s的速度竖直上抛,那么经过 x s物体离地
面的高度(单位:m)为10x-4.9x2.
你能根据上述规律求出物体经过多少秒落回地面吗(精确到0.01s)
分析:设物体经过 x s落回地面,这时它离地面的高度为0 m ,即
10x-4.9x2 =0 ①
一 因式分解法解一元二次方程
新知学习
思考:1.能否用配方法和公式法解方程10x - 4.9x 2 = 0?
2.除配方法、公式法外,能否找到更简单的方法?
10x - 4.9x 2 = 0
解:因式分解,得
x (10 - 4.9x) = 0
于是得
x = 0 或 10 - 4.9x = 0
一移-----方程的右边=0
二分-----方程的左边因式分解
三化-----方程化为两个一元一次方程
四解-----写出方程两个解
依据:如果a·b=0,那么a=0或b=0.
这种通过因式分解,将一个一元二次方程转化为两个一元一次方程求解的方法叫做因式分解法.
因式分解法的概念
因式分解法的基本步骤
一移——方程的右边 = 0;
二分——方程的左边因式分解;
三化——方程化为两个一元一次方程;
四解——写出方程的两个解.
简记歌诀:
右化零 左分解
两因式 各求解
针对训练
1.解下列方程:
解:因式分解,得
于是得
x-2=0或x+1=0,
x1=2,x2=-1.
(x-2)(x+1)=0.
解:移项、合并同类项,得
因式分解,得
( 2x+1)( 2x-1 )=0.
于是得
2x+1=0或2x-1=0,
解:化为一般式为
x2-2x+1 = 0.
因式分解,得
(x-1)(x-1) = 0.
有 x - 1 = 0 或 x - 1 = 0,
x1=x2=1.
解:因式分解,得
有 x = 0 或 ,
例 选择合适的方法解方程:
(1)3x(2x+1)=4x+2
二 选择合适的方法解一元二次方程
因式分解最优
(2)(2x-3)2=(3x-2)2
因式分解法:
解:移项,得(2x-3)2-(3x-2)2 =0.
因式分解,得
[(2x-3)+(3x-2)][(2x-3)-(3x-2)]=0.
即(5x-5)(-x-1)=0,
∴5x-5=0,或-x-1=0,
∴x1=1,x2=-1.
直接开平方法:
解:两边直接开平方,得
2x-3=±(3x-2) ,
于是得
2x-3=3x-2 ,2x-3=-3x+2
∴x1=-1,x2=1.
(2)(2x-3)2=(3x-2)2
公式法:
解:方程化为x2-1=0.
a=1,b=0,c=-1.
b2-4ac=4>0.
方程有两个不等的实数根
即
(3) x2 - 12x = 4
配方法:
解: x2 - 12x + 62 = 4 + 62,
即 (x - 6)2 = 40.
开平方,得
解得 x1= ,
x2=
直接开平方最优
(3) x2 - 12x = 4
公式法:
解:方程化为x2 - 12x-4=0.
a=1,b=-12,c=-4.
b2-4ac=(-12) -4×1×(-4)=160>0.
方程有两个不等的实数根
即
(4) 3x2 = 4x + 1
公式法:
解:方程化为3x2 - 4x-1=0.
a=3,b=-4,c=-1.
b2-4ac=(-4) -4×3×(-1)=28>0.
方程有两个不等的实数根
即
配方法最优
(4) 3x2 = 4x + 1
配方法:
解:移项,系数化为1,得
即
如何选择最简单的方法,解一元二次方程?
公式法最优
方法 适用方程 适用特点
直接开平方法 ax2+c =0(m≠0,ac<0) (x+m) =n(n≥0) 一次项系数为0或左右两边能直接开平方
因式分解法 ax +bx+=0(a≠0) (mx+n)(dx+e)=0(m,d≠0) 方程求解过程中,等式两边不能同时约去含有相同未知数的因式
公式法 所有一元二次方程(b -4ac≥0) 把式子化成一般形式,方程的右边一定要化为0
配方法 x +px+q=0(p -4p≥0) 二次项系数化为1后,一次项系数是偶数的一元二次方程,且各项系数比较小,便于配方
归纳
思路:都是降次,将一元二次方程转化为一元一次方程解决
针对训练
1.将下列序号填到对应的横线上.
① x2-3x+1=0 ; ② 3x2-1=0 ; ③ -3t2+t=0 ; ④ x2-4x=2 ;
⑤ 2x2-x=0; ⑥ 5(m+2)2=8;⑦ 3y2-y-1=0; ⑧ 2x2+4x-1=0;
⑨ (x-2)2=2(x-2).
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
②
⑥
③
⑤
⑨
①
⑦
⑧
④
1. 请选择你认为适当的方法解下列方程.
(1)(x+4) =4x +1-4x (2)x -4x-1=0
直接开平方法:
解:整理,得
(x+4) =(2x-1)
x+4=±(2x-1)
x+4=2x-1或x+4=-2x+1
即
配方法:
解:
随堂练习
即
(3)2x +x-1=0 (4)x -3x=0
公式法:
解:a=2,b=1,c=-1.
b2-4ac=1 -4×2×(-1)=7>0.
方程有两个不等的实数根
即
所以x=0,或x-3=0
即
因式分解法:
解: x(x-3)=0
2.改错
(2x+3)(x-2)=(x-2)
解:2x+3 =1 ①
2x= -2 ②
x= -1 ③
上述过程从第______步开始出错,请你写出正确的解决过程.
①
改:
解:(2x+3)(x-2)=(x-2),
(2x+3)(x-2)-(x-2)=0,
(2x+2)(x-2)=0,
2x+2=0或 x-2=0
即
3. 把小圆形场地的半径增加5m得到大圆形场地,场地面积增加到原来的2倍,求小圆形场地的半径.
解:设小圆形场地的半径为r,
根据题意 ( r + 5 )2π=2r2π.
因式分解,得
于是得
答:小圆形场地的半径为
4.一个等腰三角形的底边长是 6,腰长是一元二次方程
x2-8x + 15=0 的一根,则此三角形的周长是___________
16
(x-3)(x-5)2=0
概念
步骤
简记歌诀:
右化零 左分解
两因式 各求解
如果a ·b=0,那么a=0或b=0.
原理
当右边=0时,将方程左边因式分解.
a(x+m)(x+n)=0
(mx+n)(dx+e)=0(m,d≠0)
因式分解法
课堂小结
直接开平方法
所有一元二次方程
(b -4ac≥0)
ax2+c =0(m≠0,ac<0)
(x+m) =n(n≥0)
一次项系数为0或左右两边能
直接开平方
一元二次
方程解法
因式分解法
ax +bx+=0(a≠0)
(mx+n)(dx+e)=0(m,d≠0)
方程求解过程中,等式两边
不能同时约去含有相同未知
数的因式
公式法
把式子化成一般形式,方
程的右边一定要化为0
配方法
x +px+q=0(p -4p≥0)
把二次项系数化为1后,
一次项系数是偶数的一元
二次方程,且各项系数比
较小,便于配方
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
