21.1一元二次方程 课件 (共34张PPT)
文档属性
| 名称 | 21.1一元二次方程 课件 (共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
人教九上数学同步精品课件
人教版九年级上册
21.1 一元二次方程
4
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解一元二次方程的概念及一元二次方程根的意义;
3.理解并灵活运用一元二次方程概念解决有关问题.
重点
难点
学习目标
设计师在设计人体雕像时,使雕像的上部 AC (腰以上)与下部 BC (腰以下)的高度比,等于下部 BC 与全部 AB (全身)的高度比,可以增加视觉美感. 按此比例,如果雕像的高 AB 为 2m,下部 BC = x m,请列出方程.
A
C
B
(2 - x ) m
x m
新课引入
如图,雕像的上部高度AC 与下部高度BC应有如下关系:
AC∶BC = BC∶2,即 BC2 = 2AC.
设雕像下部高 x m,可得方程 x2 = 2(2 - x),
整理得 :
x2+2x - 4=0.
A
C
B
(2 - x ) m
x m
想一想,这个方程与我们学过的一元一次方程有什么不同,它应该叫什么?
如何解这类方程?
这类方程在生活中有哪些应用?
问题1 如图, 有一块矩形铁皮,长 100cm,宽 50cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为 3600cm2,那么铁皮各角应切去多大的正方形?
新知学习
长:(100-2x)cm 宽:(50-2x)cm
长 × 宽 = 3600
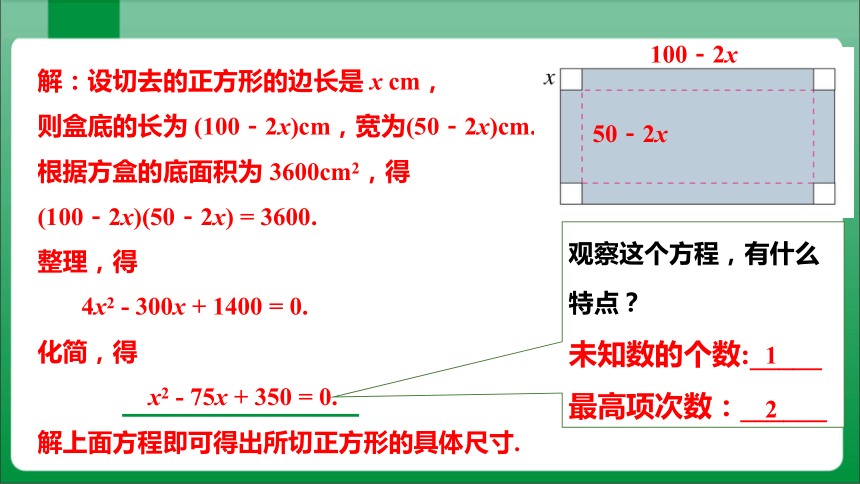
解:设切去的正方形的边长是 x cm,
则盒底的长为 (100-2x)cm,宽为(50-2x)cm.
根据方盒的底面积为 3600cm2,得
(100-2x)(50-2x) = 3600.
整理,得
4x2 - 300x + 1400 = 0.
化简,得
x2 - 75x + 350 = 0.
解上面方程即可得出所切正方形的具体尺寸.
50-2x
100-2x
观察这个方程,有什么特点?
未知数的个数:_____
最高项次数:______
1
2
问题2 要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
A,B两队只需比赛一场,算场次要÷2
x个队共有几场比赛?
共进行
场比赛
思考
设应邀请 x 个队参赛,则每个队要与其他 (x - 1) 个队各赛一场,因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,
列方程
整理,得
化简,得
解左边方程即可得出参赛队数.
解:全部比赛场数为 .
所以全部比赛共 场.
1.方程 , , 有什么共同点?
思考
1、等号的两边都是整式
2、只含有一个未知数
3、未知数的最高次数是2次
2.同学们,你能根据上面的思考说出什么一元二次方程的概念吗
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.
一元二次方程的一般形式是
ax2+bx +c = 0 (a,b,c为常数,a≠0)
ax2 称为二次项, a 称为二次项系数,
bx 称为一次项, b 称为一次项系数,
c 称为常数项.
归纳
为什么a≠0呢?
若a=0,方程ax2+bx +c = 0 变为bx +c = 0,等式中无二次项,不满足一元二次方程的条件,则不是一元二次方程.
对于一元二次方程的一般形式ax2+bx +c = 0 (a,b,c为常数,a≠0)而言,b和c能不能等于0?
可以,因为b和c等于0不影响一元二次方程的判定:
1、等号的两边都是整式
2、只含有一个未知数
3、未知数的最高次数是2次
例 判断下列方程是否为一元二次方程,如果是,请将方程化为一般形式,并指出二次项系数、一次项系数以及常数项.
(1)
(2)
(3) 3x = 5
是一元二次方程,一般形式为3x2-5=0,二次项系数 3,一次项系数为0,常数项为-5.
是一元二次方程,一般形式为 , 二次项系数为 ,一次项系数 2,常数项为 -10.
不是一元二次方程,因为等式左边不是是整式.
(4)x2+y-6 = 0
不是一元二次方程,未知数有两个
(5)x2-2+5x3-6x = 0
不是一元二次方程,未知数的最高次数是3次
(6)-7x2-6x + 6 = 6
是一元二次方程,一般形式为-7x2-6x = 0, 二次项系数为-7 ,一次项系数 为 - 6,常数项为 0.
判别方法总结:
一化:先化简,拆括号
二移:将所有项移到等式左边,等式右边为0
三合:合并同类型
四看:看是否只含有一个未知数,未知数的最高次数是否为2
(4)
(5)2x2-3x = 2(x2-2)
不是一元二次方程,因为一般形式为-3x+4 = 0,未知数的最高次数是1次
是一元二次方程,一般形式为3x2-8x-10 = 0, 二次项系数为3 ,一次项系数 为 - 8,常数项为 -10.
x2 - x - 3=0
对于引入的这个方程,我们发现当x取-1或2的时候可以使得等号两边相等,那么我们称这两个值就是此一元二次方程的解.
定义:使一元二次方程等号两边相等的未知数的值叫做一元二次方程的解(又叫做一元二次方程的根).
二、一元二次方程的根
例1 验证x=5是否为 的根.
x2-75x+350=0
解:将x=5代入方程x2-75x+350 = 0中,
左边=5 -75×5+350=25-375+350=0,
右边=0.
∵左边=右边,
∴x=5是一元二次方程x2-75x+350 = 0的根.
例2 如果2是方程
方程的其他根.
x2-c = 0的一个根,那么常数c是多少?求出这个
解:将x=2代入方程x2-c = 0中,
2 -c=0,
∴c=4,方程为x2-4= 0
∴x2 = 4,x=±2
∴这个方程另外的根是-2
定义:一元二次方程是刻画现实世界的一个有效数学模型,它是把实际问题中语言叙述的数量关系通过设未知数用一元二次方程来表达,然后解方程,从而达到解决实际问题的目的.
三、建立一元二次方程模型(思想)
圆形的面积问题 增长(利润)率
行程问题 工程问题等
常用于一元二次方程来建模的问题有:
例 如图,在一块长12 m,宽8 m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为77 m2.设道路的宽为x m,则根据题意,可列方程为_________.
怎么表示出栽种花草部分的面积呢?
思路点拨:
1.若设小路的宽是xm,则横向小路的面积是______m2,纵向小路的面积是_______m2,两者重叠的面积是 m2.
8x
12x
x2
2.由于栽种花草的面积为77 m2.你能列出方程吗?
总面积-小路面积+重叠部分面积=栽种花草面积
8×12-8x-12x+x2=77
x2 - 20x+19=0
8m
还有其他方法吗?
(8-x)(12-x)=77
x2 - 20x+19=0
针对训练
1.根据下列问题,列出关于 x 的方程,并将所列方程化成一元二次方程的一般形式:
(1) 4个完全相同的正方形的面积之和是 25,求正方形的边长 x;
解:(1)由题意得,4x2 = 25,化成一般式为4x2 – 25 = 0;
(2)一个矩形的长比宽多 2,面积是 100,求矩形的长 x ;
(2)由题意得,x(x - 2) = 100,化成一般式为 x2 - 2x - 100 = 0;
(3)把长为 1 的木条分成两段,使较短一段的长与全长的积,等于较长一段的长的平方,求较短一段的长 x.
(3)由题意得,x = (1-x)2,化成一般式为x2 - 3x + 1 = 0.
1.将下列方程化成一元二次方程的一般式,并写出其中的二次项系数、一次项系数合常数项.
随堂练习
(1)
一般形式为 , 二次项系数为3,一次项系数 -6
(2)
一般形式为 , 二次项系数为4,一次项系数 5
(3)
一般形式为 , 二次项系数为1,一次项系数 5
(4)
一般形式为 , 二次项系数为2,一次项系数 -4
(5)
一般形式为 , 二次项系数为1,一次项系数 0
(6)
一般形式为 , 二次项系数为1,一次项系数 2
2.下列哪些数是方程 x2 + x – 12 = 0的根?
-4,-3,-2,-1,0,1,2,3,4
解:当 x = -4 时,左边 = 16+(-4) – 12 = 0,则左边 = 右边,
所以 -4 是方程 x2 + x – 12 = 0 的解;
当 x = 3 时,左边 = 16+3 – 12 = 0,则左边 = 右边,
所以 -4 是方程 x2 + x – 12 = 0 的解;
因为其他几个数不能满足方程左右两边相等,所以不是该方程的根所以可得 -4,3 为原方程的根.
3.参加一次聚会的每两人都握一次手,所有人共握手10次,有多少人参加聚会?
解:设参加聚会的有x人,则:
因为人数不能取负,所以 - 4 舍去,共有5人参加聚会.
4.关于x的方程(m-1)xlml+1+2mx+2=0是一元二次方程,则m的值为多少?
解:由题意得:
∴ m= -1
5.已知m是方程x2-x-1=0的一个根,
(1)求代数式5m2-5m+1001的值;
(2)求 的值
解:(1)将x=m代入方程x2-x-1=0可得:m2-m-1=0,即m2-m=1.
原式=5(m2-m)+1001=1006.
(2)由已知可得:m2-m=1.代入原式得:
原式=
一般形式
根
概念
ax2+bx+c=0 (a,b,c为常数,且a ≠0)
①等号左右两边都是整式
②只含有一个未知数
③未知数的最高次数是2次
使方程左右两边相等的未知数的值
审→设→找→列
一元二次方程
建立一元二次方程模型
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
21.1 一元二次方程
4
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解一元二次方程的概念及一元二次方程根的意义;
3.理解并灵活运用一元二次方程概念解决有关问题.
重点
难点
学习目标
设计师在设计人体雕像时,使雕像的上部 AC (腰以上)与下部 BC (腰以下)的高度比,等于下部 BC 与全部 AB (全身)的高度比,可以增加视觉美感. 按此比例,如果雕像的高 AB 为 2m,下部 BC = x m,请列出方程.
A
C
B
(2 - x ) m
x m
新课引入
如图,雕像的上部高度AC 与下部高度BC应有如下关系:
AC∶BC = BC∶2,即 BC2 = 2AC.
设雕像下部高 x m,可得方程 x2 = 2(2 - x),
整理得 :
x2+2x - 4=0.
A
C
B
(2 - x ) m
x m
想一想,这个方程与我们学过的一元一次方程有什么不同,它应该叫什么?
如何解这类方程?
这类方程在生活中有哪些应用?
问题1 如图, 有一块矩形铁皮,长 100cm,宽 50cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为 3600cm2,那么铁皮各角应切去多大的正方形?
新知学习
长:(100-2x)cm 宽:(50-2x)cm
长 × 宽 = 3600
解:设切去的正方形的边长是 x cm,
则盒底的长为 (100-2x)cm,宽为(50-2x)cm.
根据方盒的底面积为 3600cm2,得
(100-2x)(50-2x) = 3600.
整理,得
4x2 - 300x + 1400 = 0.
化简,得
x2 - 75x + 350 = 0.
解上面方程即可得出所切正方形的具体尺寸.
50-2x
100-2x
观察这个方程,有什么特点?
未知数的个数:_____
最高项次数:______
1
2
问题2 要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
A,B两队只需比赛一场,算场次要÷2
x个队共有几场比赛?
共进行
场比赛
思考
设应邀请 x 个队参赛,则每个队要与其他 (x - 1) 个队各赛一场,因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,
列方程
整理,得
化简,得
解左边方程即可得出参赛队数.
解:全部比赛场数为 .
所以全部比赛共 场.
1.方程 , , 有什么共同点?
思考
1、等号的两边都是整式
2、只含有一个未知数
3、未知数的最高次数是2次
2.同学们,你能根据上面的思考说出什么一元二次方程的概念吗
等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.
一元二次方程的一般形式是
ax2+bx +c = 0 (a,b,c为常数,a≠0)
ax2 称为二次项, a 称为二次项系数,
bx 称为一次项, b 称为一次项系数,
c 称为常数项.
归纳
为什么a≠0呢?
若a=0,方程ax2+bx +c = 0 变为bx +c = 0,等式中无二次项,不满足一元二次方程的条件,则不是一元二次方程.
对于一元二次方程的一般形式ax2+bx +c = 0 (a,b,c为常数,a≠0)而言,b和c能不能等于0?
可以,因为b和c等于0不影响一元二次方程的判定:
1、等号的两边都是整式
2、只含有一个未知数
3、未知数的最高次数是2次
例 判断下列方程是否为一元二次方程,如果是,请将方程化为一般形式,并指出二次项系数、一次项系数以及常数项.
(1)
(2)
(3) 3x = 5
是一元二次方程,一般形式为3x2-5=0,二次项系数 3,一次项系数为0,常数项为-5.
是一元二次方程,一般形式为 , 二次项系数为 ,一次项系数 2,常数项为 -10.
不是一元二次方程,因为等式左边不是是整式.
(4)x2+y-6 = 0
不是一元二次方程,未知数有两个
(5)x2-2+5x3-6x = 0
不是一元二次方程,未知数的最高次数是3次
(6)-7x2-6x + 6 = 6
是一元二次方程,一般形式为-7x2-6x = 0, 二次项系数为-7 ,一次项系数 为 - 6,常数项为 0.
判别方法总结:
一化:先化简,拆括号
二移:将所有项移到等式左边,等式右边为0
三合:合并同类型
四看:看是否只含有一个未知数,未知数的最高次数是否为2
(4)
(5)2x2-3x = 2(x2-2)
不是一元二次方程,因为一般形式为-3x+4 = 0,未知数的最高次数是1次
是一元二次方程,一般形式为3x2-8x-10 = 0, 二次项系数为3 ,一次项系数 为 - 8,常数项为 -10.
x2 - x - 3=0
对于引入的这个方程,我们发现当x取-1或2的时候可以使得等号两边相等,那么我们称这两个值就是此一元二次方程的解.
定义:使一元二次方程等号两边相等的未知数的值叫做一元二次方程的解(又叫做一元二次方程的根).
二、一元二次方程的根
例1 验证x=5是否为 的根.
x2-75x+350=0
解:将x=5代入方程x2-75x+350 = 0中,
左边=5 -75×5+350=25-375+350=0,
右边=0.
∵左边=右边,
∴x=5是一元二次方程x2-75x+350 = 0的根.
例2 如果2是方程
方程的其他根.
x2-c = 0的一个根,那么常数c是多少?求出这个
解:将x=2代入方程x2-c = 0中,
2 -c=0,
∴c=4,方程为x2-4= 0
∴x2 = 4,x=±2
∴这个方程另外的根是-2
定义:一元二次方程是刻画现实世界的一个有效数学模型,它是把实际问题中语言叙述的数量关系通过设未知数用一元二次方程来表达,然后解方程,从而达到解决实际问题的目的.
三、建立一元二次方程模型(思想)
圆形的面积问题 增长(利润)率
行程问题 工程问题等
常用于一元二次方程来建模的问题有:
例 如图,在一块长12 m,宽8 m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为77 m2.设道路的宽为x m,则根据题意,可列方程为_________.
怎么表示出栽种花草部分的面积呢?
思路点拨:
1.若设小路的宽是xm,则横向小路的面积是______m2,纵向小路的面积是_______m2,两者重叠的面积是 m2.
8x
12x
x2
2.由于栽种花草的面积为77 m2.你能列出方程吗?
总面积-小路面积+重叠部分面积=栽种花草面积
8×12-8x-12x+x2=77
x2 - 20x+19=0
8m
还有其他方法吗?
(8-x)(12-x)=77
x2 - 20x+19=0
针对训练
1.根据下列问题,列出关于 x 的方程,并将所列方程化成一元二次方程的一般形式:
(1) 4个完全相同的正方形的面积之和是 25,求正方形的边长 x;
解:(1)由题意得,4x2 = 25,化成一般式为4x2 – 25 = 0;
(2)一个矩形的长比宽多 2,面积是 100,求矩形的长 x ;
(2)由题意得,x(x - 2) = 100,化成一般式为 x2 - 2x - 100 = 0;
(3)把长为 1 的木条分成两段,使较短一段的长与全长的积,等于较长一段的长的平方,求较短一段的长 x.
(3)由题意得,x = (1-x)2,化成一般式为x2 - 3x + 1 = 0.
1.将下列方程化成一元二次方程的一般式,并写出其中的二次项系数、一次项系数合常数项.
随堂练习
(1)
一般形式为 , 二次项系数为3,一次项系数 -6
(2)
一般形式为 , 二次项系数为4,一次项系数 5
(3)
一般形式为 , 二次项系数为1,一次项系数 5
(4)
一般形式为 , 二次项系数为2,一次项系数 -4
(5)
一般形式为 , 二次项系数为1,一次项系数 0
(6)
一般形式为 , 二次项系数为1,一次项系数 2
2.下列哪些数是方程 x2 + x – 12 = 0的根?
-4,-3,-2,-1,0,1,2,3,4
解:当 x = -4 时,左边 = 16+(-4) – 12 = 0,则左边 = 右边,
所以 -4 是方程 x2 + x – 12 = 0 的解;
当 x = 3 时,左边 = 16+3 – 12 = 0,则左边 = 右边,
所以 -4 是方程 x2 + x – 12 = 0 的解;
因为其他几个数不能满足方程左右两边相等,所以不是该方程的根所以可得 -4,3 为原方程的根.
3.参加一次聚会的每两人都握一次手,所有人共握手10次,有多少人参加聚会?
解:设参加聚会的有x人,则:
因为人数不能取负,所以 - 4 舍去,共有5人参加聚会.
4.关于x的方程(m-1)xlml+1+2mx+2=0是一元二次方程,则m的值为多少?
解:由题意得:
∴ m= -1
5.已知m是方程x2-x-1=0的一个根,
(1)求代数式5m2-5m+1001的值;
(2)求 的值
解:(1)将x=m代入方程x2-x-1=0可得:m2-m-1=0,即m2-m=1.
原式=5(m2-m)+1001=1006.
(2)由已知可得:m2-m=1.代入原式得:
原式=
一般形式
根
概念
ax2+bx+c=0 (a,b,c为常数,且a ≠0)
①等号左右两边都是整式
②只含有一个未知数
③未知数的最高次数是2次
使方程左右两边相等的未知数的值
审→设→找→列
一元二次方程
建立一元二次方程模型
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
