人教版九年级数学上册22.3实际问题与二次函数 课件(共16张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.3实际问题与二次函数 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 851.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 21:35:24 | ||
图片预览






文档简介
(共16张PPT)
第二十二章 二次函数
实际问题与二次函数
问题 1 二次函数 的图象和性质
①当 a > 0 时,二次函数的图象(抛物线)开口______,有最______点,对称轴是____,顶点坐标是______ ;
②当 a < 0 时,二次函数的图象(抛物线)开口______,有最______点,对称轴是____ ,顶点坐标是______.
(2)二次函数 的图象和性质
①当 a > 0 时,二次函数的图象(抛物线)开口______,有最______点,对称轴是____,顶点坐标是______;
②当 a < 0 时,二次函数的图象(抛物线)开口______,有最______点,对称轴是____,顶点坐标是______.
一、创设情境,引入新知
某商店销售一种商品,每件的进价为 2.50 元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.50 元时,销售量为 500 件,而单价每降低 1 元,就可以多售出200 件. 你知道销售单价定为多少元时,商店获利最大吗?
一、创设情境,引入新知
问题 2
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是 (0 ≤ t ≤ 6). 小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
二、合作交流,探究新知
问题 3
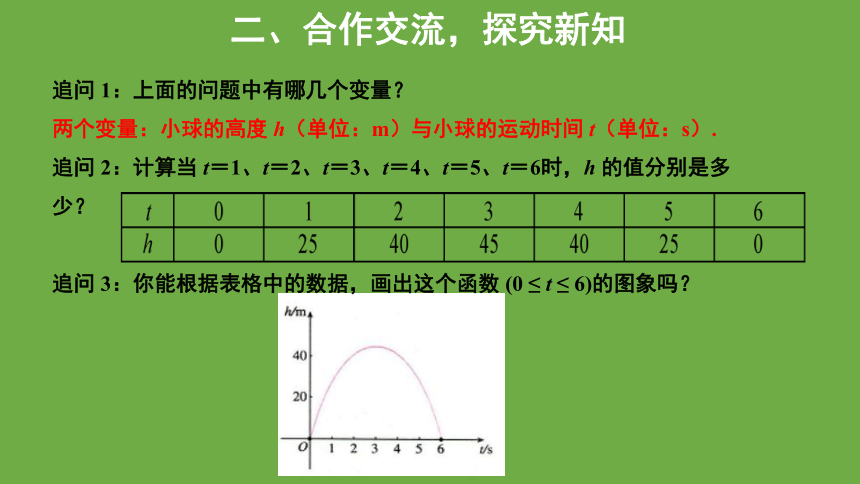
追问 1:上面的问题中有哪几个变量?
两个变量:小球的高度 h(单位:m)与小球的运动时间 t(单位:s).
追问 2:计算当 t=1、t=2、t=3、t=4、t=5、t=6时,h 的值分别是多少?
追问 3:你能根据表格中的数据,画出这个函数 (0 ≤ t ≤ 6)的图象吗?
二、合作交流,探究新知
追问 4:根据函数图象,观察出小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
归纳:这个函数的图象是一条抛物线的一部分.这条抛物线的顶点是这个函数的图象的最高点,也就是说,当t取顶点的横坐标时,这个函数有最大值.
追问 5:能直接根据函数的解析式求出它的顶点坐标和最大值吗?
追问 6:对于一般形式的二次函数 的最小(大)值又是怎么的呢?
归纳:当a>0(a<0),抛物线 的顶点是最低(高)点,也就是说,当 时,二次函数有最小(大)值 .
二、合作交流,探究新知
例 1:用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化. 当 l 是多少米时,场地的面积 S 最大?
分析:先找出两个变量,然后写出 S 关于 l 的函数解析式,最后求出使
S 最大的 l 值.
三、运用新知
例 2:某商品现在的售价为每件 60 元,每星期可卖出 300 件. 市场调查反映:如调整价格,每涨价 1 元,每星期要少卖出 10 件;每降价 1 元,每星期可多卖出 20 件. 已知商品的进价为每件 40 元,如何定价才能使利润最大?
三、运用新知
分析:调整的价格包括涨价和降价两种情况.
(1)我们先看涨价的情况.
设每件涨价 x 元,每星期则少卖 l0x 件,实际卖出 (300-l0x) 件,销售额为(60 + x) (300-l0x) 元,买进商品需付 40(300-10x) 元. 因此,所得利润
y = (60+x)(300-l0x)一40(300-l0x),
即 .
列出函数解析式后,引导学生怎样确定 x 的取值范围呢?
由 300-l0x ≥ 0,得 x ≤ 30. 再由 x ≥ 0 ,得 0 ≤ x ≤ 30.
根据上面的函数,可知:当 x = 5 时,y 最大,也就是说,在涨价的情况下,涨价 5 元,即定价 65 元时,利润最大,最大利润是 6250 元.
三、运用新知
(2)我们再看降价的情况.
设每件降价 x 元,每星期则多卖 20x 件,实际卖出 (300+20x) 件,销售额为
(60-x) (300+20x) 元,买进商品需付 40(300+20x) 元.因此,所得利润
y = (60-x)(300+20x)-40(300+20x),
即 .
怎样确定 x 的取值范围呢?
由降价后的定价 (60-x) 元,不高于现价 60 元,不低于进价 40 元可得 0 ≤ x ≤ 20.
当 x = 2.5 时,y 最大,也就是说,在降价的情况下,降价 2.5 元,即定价 57.5 元时,利润最大,最大利润是 6125 元.
三、运用新知
由(1)(2)的讨论及现在的销售状况,你知道应如何定价能使利润最大了吗?
结论:综合涨价和降价两种情况及现在的销售状况可知,定价 65 元时,利润最大.
追问:现在可以解决课前提出的问题 2 中的最大利润问题了吗?
分析: 设每件商品降价 x 元,总利润为 y 元,则
y = (13.5-x-2.5)(500+200x),即 ,顶点坐标为(4.25,9112.5),即当每件商品降价 4.25 元,即售价为
13.5-4.25 = 9.25时,可取得最大利润 9112.5 元.
三、运用新知
例 3:下图中是抛物线形拱桥,当拱顶离水面 2m 时,水面宽 4m.水面下降 1m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适应的坐标系,就可以求出这条抛物线表示的二次函数. 为解题简便,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
三、运用新知
已知:正方形 ABCD 的边长为 4,E 是 BC 上任意一点,且 AE = AF,若 EC = x,请写出 △AEF 的面积 y 与 x 之间的函数关系式,并求出 x为何值时 y 最大.
四、巩固新知
某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水. 连喷头在内,柱高为0.8m.水流在各个方向上沿形状相同的抛物线路径落下,如左图所示.
根据设计图纸已知:如右图中所示直角坐标系中,水流喷出的高度 y (m)与水平距离
x (m)之间的函数关系式是 .
(1)喷出的水流距水平面的最大高度是多少
(2)如果不计其他的因素,那么水池至少为多少时,才能使喷出的水流都落在水池内
四、巩固新知
师生共同回顾本节内容,并请学生回答下列问题:
1. 本节课学习了哪些主要内容?
2. 本节课你有什么收获和体会?
3. 对本节课所学知识你还有哪些疑惑?
运用二次函数解决实际问题,首先要用二次函数表示问题中变量之间的关系,然后利用二次函数的图象与性质求解,从而获得实际问题的答案.
五、归纳小结
再 见
第二十二章 二次函数
实际问题与二次函数
问题 1 二次函数 的图象和性质
①当 a > 0 时,二次函数的图象(抛物线)开口______,有最______点,对称轴是____,顶点坐标是______ ;
②当 a < 0 时,二次函数的图象(抛物线)开口______,有最______点,对称轴是____ ,顶点坐标是______.
(2)二次函数 的图象和性质
①当 a > 0 时,二次函数的图象(抛物线)开口______,有最______点,对称轴是____,顶点坐标是______;
②当 a < 0 时,二次函数的图象(抛物线)开口______,有最______点,对称轴是____,顶点坐标是______.
一、创设情境,引入新知
某商店销售一种商品,每件的进价为 2.50 元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.50 元时,销售量为 500 件,而单价每降低 1 元,就可以多售出200 件. 你知道销售单价定为多少元时,商店获利最大吗?
一、创设情境,引入新知
问题 2
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是 (0 ≤ t ≤ 6). 小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
二、合作交流,探究新知
问题 3
追问 1:上面的问题中有哪几个变量?
两个变量:小球的高度 h(单位:m)与小球的运动时间 t(单位:s).
追问 2:计算当 t=1、t=2、t=3、t=4、t=5、t=6时,h 的值分别是多少?
追问 3:你能根据表格中的数据,画出这个函数 (0 ≤ t ≤ 6)的图象吗?
二、合作交流,探究新知
追问 4:根据函数图象,观察出小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
归纳:这个函数的图象是一条抛物线的一部分.这条抛物线的顶点是这个函数的图象的最高点,也就是说,当t取顶点的横坐标时,这个函数有最大值.
追问 5:能直接根据函数的解析式求出它的顶点坐标和最大值吗?
追问 6:对于一般形式的二次函数 的最小(大)值又是怎么的呢?
归纳:当a>0(a<0),抛物线 的顶点是最低(高)点,也就是说,当 时,二次函数有最小(大)值 .
二、合作交流,探究新知
例 1:用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化. 当 l 是多少米时,场地的面积 S 最大?
分析:先找出两个变量,然后写出 S 关于 l 的函数解析式,最后求出使
S 最大的 l 值.
三、运用新知
例 2:某商品现在的售价为每件 60 元,每星期可卖出 300 件. 市场调查反映:如调整价格,每涨价 1 元,每星期要少卖出 10 件;每降价 1 元,每星期可多卖出 20 件. 已知商品的进价为每件 40 元,如何定价才能使利润最大?
三、运用新知
分析:调整的价格包括涨价和降价两种情况.
(1)我们先看涨价的情况.
设每件涨价 x 元,每星期则少卖 l0x 件,实际卖出 (300-l0x) 件,销售额为(60 + x) (300-l0x) 元,买进商品需付 40(300-10x) 元. 因此,所得利润
y = (60+x)(300-l0x)一40(300-l0x),
即 .
列出函数解析式后,引导学生怎样确定 x 的取值范围呢?
由 300-l0x ≥ 0,得 x ≤ 30. 再由 x ≥ 0 ,得 0 ≤ x ≤ 30.
根据上面的函数,可知:当 x = 5 时,y 最大,也就是说,在涨价的情况下,涨价 5 元,即定价 65 元时,利润最大,最大利润是 6250 元.
三、运用新知
(2)我们再看降价的情况.
设每件降价 x 元,每星期则多卖 20x 件,实际卖出 (300+20x) 件,销售额为
(60-x) (300+20x) 元,买进商品需付 40(300+20x) 元.因此,所得利润
y = (60-x)(300+20x)-40(300+20x),
即 .
怎样确定 x 的取值范围呢?
由降价后的定价 (60-x) 元,不高于现价 60 元,不低于进价 40 元可得 0 ≤ x ≤ 20.
当 x = 2.5 时,y 最大,也就是说,在降价的情况下,降价 2.5 元,即定价 57.5 元时,利润最大,最大利润是 6125 元.
三、运用新知
由(1)(2)的讨论及现在的销售状况,你知道应如何定价能使利润最大了吗?
结论:综合涨价和降价两种情况及现在的销售状况可知,定价 65 元时,利润最大.
追问:现在可以解决课前提出的问题 2 中的最大利润问题了吗?
分析: 设每件商品降价 x 元,总利润为 y 元,则
y = (13.5-x-2.5)(500+200x),即 ,顶点坐标为(4.25,9112.5),即当每件商品降价 4.25 元,即售价为
13.5-4.25 = 9.25时,可取得最大利润 9112.5 元.
三、运用新知
例 3:下图中是抛物线形拱桥,当拱顶离水面 2m 时,水面宽 4m.水面下降 1m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适应的坐标系,就可以求出这条抛物线表示的二次函数. 为解题简便,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
三、运用新知
已知:正方形 ABCD 的边长为 4,E 是 BC 上任意一点,且 AE = AF,若 EC = x,请写出 △AEF 的面积 y 与 x 之间的函数关系式,并求出 x为何值时 y 最大.
四、巩固新知
某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水. 连喷头在内,柱高为0.8m.水流在各个方向上沿形状相同的抛物线路径落下,如左图所示.
根据设计图纸已知:如右图中所示直角坐标系中,水流喷出的高度 y (m)与水平距离
x (m)之间的函数关系式是 .
(1)喷出的水流距水平面的最大高度是多少
(2)如果不计其他的因素,那么水池至少为多少时,才能使喷出的水流都落在水池内
四、巩固新知
师生共同回顾本节内容,并请学生回答下列问题:
1. 本节课学习了哪些主要内容?
2. 本节课你有什么收获和体会?
3. 对本节课所学知识你还有哪些疑惑?
运用二次函数解决实际问题,首先要用二次函数表示问题中变量之间的关系,然后利用二次函数的图象与性质求解,从而获得实际问题的答案.
五、归纳小结
再 见
同课章节目录
