2015连线中考数学一轮复习系列专题7:一元二次方程
文档属性
| 名称 | 2015连线中考数学一轮复习系列专题7:一元二次方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 875.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-09 00:00:00 | ||
图片预览




文档简介
基础知识
知识点一、一元二次方程的概念
只含有一个未知数(一元),且未知数的最高 ( http: / / www.21cnjy.com )次数是2(二次),这样的整式方程叫一元二次方程.一元二次方程的三个特征:①一个未知数;②未知数的最高次数是2;③整式方程.
一般地,任何一个关于x的一元二次方程,经过 ( http: / / www.21cnjy.com )整理,都能化成如下一般形式ax2 +bx+c=0=0 (其中a、b、c为常数,a≠0), a是二次项系数,b是一次项系数,c为常数项.
知识点二、一元二次方程的解法
1. 开平方法 形如的一元二次方程,用直接开平方法,把一个一元二次方程转化为两个一元一次方程来解.
2. 配方法 把一个一元二次方程通过配方成形如:的形式,当n≥0时,再使用直接开平方法求解.配方的基本策略是:当二次项系数为1时,等式的两边同时加上一次项系数一半的平方.需要说明的是,配方只是一个将等式变形的过程,配方的目的是将方程转化为直接开平方法降次求解,
3. 公式法 它是解一元二次方程的一般方法.一元二次方程(a≠0)的求根公式:.
4. 因式分解法 因式分解法是将方程 ( http: / / www.21cnjy.com )右边化为0,左边分解为两个一次因式的乘积的形式,根据A·B=0,则A=0或B=0 ,将方程转化为两个一元一次方程求解.这种方法简便易行,是解一元二次方程的最常用的方法.
5. 图像法 二次函数y = ax2 +bx + c(a≠0)的图像与x轴交点的横坐标即为方程
ax2 +bx + c = 0 的解.
知识点三、一元二次方程的根的判别式
1. 一元二次方程ax2 +bx+c = 0 (a≠0)
b2 – 4ac > 0 方程有两个不相等的实数根;
b2 – 4ac = 0 方程有两个相等的实数根;
b2 – 4ac < 0 方程无实数根;
使用判别式的几点说明:
①如果说方程有实数根,即应当包括有两个不等的实数根和有两个相等的实数根两种情况,此时≥0,切勿丢掉等号;
②如果方程不是一般形式,要化为一般形式,再确定a、b、c的值;
③使用判别式的前提是方程是一元二次方程,即二次项系数a≠0,当二次项系数含字母时,解题时要加以考虑.
2. 一元二次方程根的判别式的应用主要有以下三种情况:
(1)不解方程,判定根的情况.
(2)根据方程根的情况,确定方程系数中字母的取值范围.
(3)应用判别式证明方程根的情况.
知识点四、 一元二元方程根与系数的关系
如果方程(a≠0)的两个实数根是、,那么
+=,·=.
知识点五、一元二次方程的应用
1. 列一元二次方程解应用题的步骤:
主要是审、设、列、解、检验(既要是方程的解,还要符合实际意义)、答.
2. 几种常见的一元二次方程应用问题
① 平均变化率问题:
变化率是指变化数与基数的比 ( http: / / www.21cnjy.com ).若基数为a,变化率为x,则一次变化后的值为a(1±x) ,两次变化后的值为a(1±x)2; 说明:增长用“+”,降低用“-”.
② 面积问题
解决这类问题的关键是将不规则图形分割或补全成规则图形,找出各部分面积之间的关系,利用面积计算公式列出方程
③利润问题
单个利润 = 单个售价 – 单个进价
总利润 = 单个利润×销售数量
典型例题解析
例1. 下列方程是一元二次方程的是( )
A. x2 + 4x - 1 B. kx2 +4x – 1 = 0 (k为常数)
C. (x+1)2 = x2 D. (x-2)2 = 3(x+1)
( http: / / www.21cnjy.com )
例2. (淄博)一元二次方程的根是( )
A. B.,
C., D. ,
( http: / / www.21cnjy.com )
例3. (内蒙古自治区)关于x的一元二次方程(a+1)x2-4x-1=0有两个不相等的实数根,则a的取值范围是 ( )
A.a>-5 B.a>-5且a≠-1 C.a<-5 D.a≥-5且a≠-1
( http: / / www.21cnjy.com )
例4. (南通)设α、β是一元二次方程x2+3x-7=0的两个根,则α2+4α+β=
( http: / / www.21cnjy.com )
例5. (北京)已知关于x的方程mx2-(m+2)x+2=0(m≠0).
(1)求证:方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
例6. (沈阳)某公司今年销售一种产品 ( http: / / www.21cnjy.com ),1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.
答案:设这个增长率为x.
依题意得: 20(1+x)2—20(1+x)=4.8
( http: / / www.21cnjy.com )
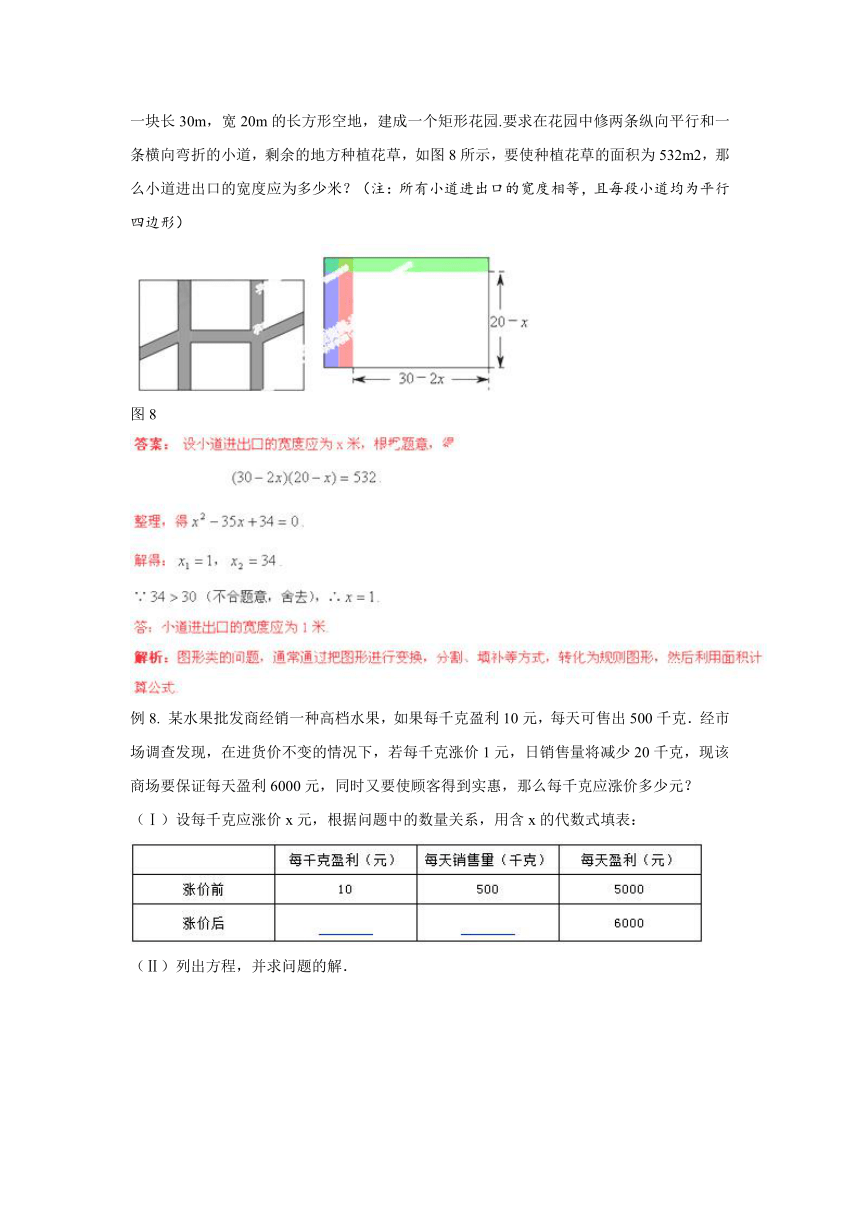
例7. (襄阳) 为响应市委市政府 ( http: / / www.21cnjy.com )提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图8所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
( http: / / www.21cnjy.com )
图8
( http: / / www.21cnjy.com )
例8. 某水果批发商经销一种高档水 ( http: / / www.21cnjy.com )果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(Ⅰ)设每千克应涨价x元,根据问题中的数量关系,用含x的代数式填表:
( http: / / www.21cnjy.com )
(Ⅱ)列出方程,并求问题的解.
( http: / / www.21cnjy.com )
巩固训练
1. 方程x(x+1)= x+1的解是( )
A.1 B.0 C.-1或0 D.1或-1
2. (聊城)用配方法解一元二次方程式ax2+bx+c=0(a≠0),此方程可变形为( )
A. B.
C. D.
3(荆州)已知α是一元二次方程x2-x-1=0较大的根,则下面对α的估计正确的是( )
A.0<α<1 B.1<α<1.5 C.1.5<α<2 D.2<α<3
4(攀枝花)若方程x2+x-1=0的两实根为α、β,那么下列说法不正确的是( )
A.α+β=-1 B.αβ=-1 C.α2+β2=3 D.+=-1
5. (天津)要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据时间和场地等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请个队参赛,则满足的关系式为( )
A. B. C. D.
6. (抚州) 关于x的一元二次方程x2-5x+k=0有两个不相等的实数根,则k可能的最大整数为 .
7. (内江)若关于x的一元二次方程(k-1) x 2+2x-2=0有不相等实数根,则k的取值范围是( )
A.k> B.k≥ C.k>且k≠1 D.k≥且k≠1
8. (丽水)如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的
通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面
积都为78,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程________.
SHAPE \* MERGEFORMAT HYPERLINK "http://www.21cnjy.com"
9. 用适当的方法解下列方程
(1)3x(x – 2)=2(2 – x) (2) x2 – 6x+8=0.
(3) 2x2 – 4x+1=0. (4) (x - 1) (x+2) = 1
10. (株洲)已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
11. (山西)某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?
( http: / / www.21cnjy.com )
12.(朝阳)长城汽车销售公司5月份销售某型 ( http: / / www.21cnjy.com )号汽车.当月该型号汽车的进价为30万元/辆,若当月销售辆超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x正为整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需要售出多少辆汽车?(注:销售利润=销售价-进价)
中考预测
1. 一元二次方程x2+px-2=0的一个根为2,则p的值为( )
A.1 B.2 C.-1 D.-2
2. 下列关于x的方程有实数根的是 ( )
A. x2-x+1=0 B. x2+x+1=0
C. (x-1)(x+2)=0 D. (x-1)2+1=0
3. 一元二次方程x2-2x+m=0有两个实数根,则m应满足的条件是( )
A.m>1 B.m=1 C.m<1 D.m≤1
4. x1,x2是一二次方程3(x-1)2=15的两个解,且x1<x2,下列说法正确的是( )
A.x1小于-1,x2大于3 B.x1小于-2,x2大于3
C.x1,x2 在-1和3之间 D.x1,x2都小于3
5. 若关于x的方程m(x ( http: / / www.21cnjy.com )+h)2+k=0(m、h、k均为常数,m≠0)的解是x1=-3,x2=2,则方程m(x+h-3)2+k=0的解 ( )
A.x1=-6,x2=-1 B.x1=0,x2=5
C.x1=-3,x2=5 D.x1=-6,x2=2
6. 某种花卉每盆的盈利与每盆的株数有一定的关系. 每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元. 要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植株,则可以列出的方程是( )
A. B.
C. D.
7. 对于实数a,b,我们定义一种运算“※”为:a※b=a2-ab,例如1※3=12-1×3.若x※4=0,则x=_________
8. 等腰三角形一条边的边长为3,它的另两条边的边长是关于x的一元二次方程x2-12x+k=0的两个根,则k的值是 .
9. 已知m、n是方程x2 –x–1=0的两实数根,则的值为 .
10. 已知关于x的方程
(1)若该方程的一个根为1,求a的值及该方程的另一根
(2)求证:不论a取何实数,该方程都有两个不相等的实数根
11. (新疆乌鲁木齐) ( http: / / www.21cnjy.com )某工厂使用旧设备生产,每月生产收入是90万元,每月另需支付设备维护费5万元;从今年1月份起使用新设备,生产收入提高且无设备维护费,使用当月生产收入达100万元,1至3月份生产收入以相同的百分率逐月增长,累计达364万元,3月份后,每月生产收入稳定在月份的水平.
⑴求使用新设备后,2月、3月生产收入的月增长率;
⑵购进新设备需一次性支付640万元,使 ( http: / / www.21cnjy.com )用新设备几个月后,该厂所得累计利润不低于使用旧设备的累计利润?(累计利润是指累计生产收入减去旧设备维护费或新设备购进费)
12. 某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.5米的正方形ABCD.点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,则中间的阴影部分组成正方形EFGH.已知烧制该种地砖平均每块需加工费0.35元,若要CE长大于0.1米,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则CE长应为多少米?
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )(2)∵方程有两个相等的实数根,
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
中考预测
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
∴x1=0.2,x2=0.05(不合题意舍去).答:CE的长应为0.2m.
知识点一、一元二次方程的概念
只含有一个未知数(一元),且未知数的最高 ( http: / / www.21cnjy.com )次数是2(二次),这样的整式方程叫一元二次方程.一元二次方程的三个特征:①一个未知数;②未知数的最高次数是2;③整式方程.
一般地,任何一个关于x的一元二次方程,经过 ( http: / / www.21cnjy.com )整理,都能化成如下一般形式ax2 +bx+c=0=0 (其中a、b、c为常数,a≠0), a是二次项系数,b是一次项系数,c为常数项.
知识点二、一元二次方程的解法
1. 开平方法 形如的一元二次方程,用直接开平方法,把一个一元二次方程转化为两个一元一次方程来解.
2. 配方法 把一个一元二次方程通过配方成形如:的形式,当n≥0时,再使用直接开平方法求解.配方的基本策略是:当二次项系数为1时,等式的两边同时加上一次项系数一半的平方.需要说明的是,配方只是一个将等式变形的过程,配方的目的是将方程转化为直接开平方法降次求解,
3. 公式法 它是解一元二次方程的一般方法.一元二次方程(a≠0)的求根公式:.
4. 因式分解法 因式分解法是将方程 ( http: / / www.21cnjy.com )右边化为0,左边分解为两个一次因式的乘积的形式,根据A·B=0,则A=0或B=0 ,将方程转化为两个一元一次方程求解.这种方法简便易行,是解一元二次方程的最常用的方法.
5. 图像法 二次函数y = ax2 +bx + c(a≠0)的图像与x轴交点的横坐标即为方程
ax2 +bx + c = 0 的解.
知识点三、一元二次方程的根的判别式
1. 一元二次方程ax2 +bx+c = 0 (a≠0)
b2 – 4ac > 0 方程有两个不相等的实数根;
b2 – 4ac = 0 方程有两个相等的实数根;
b2 – 4ac < 0 方程无实数根;
使用判别式的几点说明:
①如果说方程有实数根,即应当包括有两个不等的实数根和有两个相等的实数根两种情况,此时≥0,切勿丢掉等号;
②如果方程不是一般形式,要化为一般形式,再确定a、b、c的值;
③使用判别式的前提是方程是一元二次方程,即二次项系数a≠0,当二次项系数含字母时,解题时要加以考虑.
2. 一元二次方程根的判别式的应用主要有以下三种情况:
(1)不解方程,判定根的情况.
(2)根据方程根的情况,确定方程系数中字母的取值范围.
(3)应用判别式证明方程根的情况.
知识点四、 一元二元方程根与系数的关系
如果方程(a≠0)的两个实数根是、,那么
+=,·=.
知识点五、一元二次方程的应用
1. 列一元二次方程解应用题的步骤:
主要是审、设、列、解、检验(既要是方程的解,还要符合实际意义)、答.
2. 几种常见的一元二次方程应用问题
① 平均变化率问题:
变化率是指变化数与基数的比 ( http: / / www.21cnjy.com ).若基数为a,变化率为x,则一次变化后的值为a(1±x) ,两次变化后的值为a(1±x)2; 说明:增长用“+”,降低用“-”.
② 面积问题
解决这类问题的关键是将不规则图形分割或补全成规则图形,找出各部分面积之间的关系,利用面积计算公式列出方程
③利润问题
单个利润 = 单个售价 – 单个进价
总利润 = 单个利润×销售数量
典型例题解析
例1. 下列方程是一元二次方程的是( )
A. x2 + 4x - 1 B. kx2 +4x – 1 = 0 (k为常数)
C. (x+1)2 = x2 D. (x-2)2 = 3(x+1)
( http: / / www.21cnjy.com )
例2. (淄博)一元二次方程的根是( )
A. B.,
C., D. ,
( http: / / www.21cnjy.com )
例3. (内蒙古自治区)关于x的一元二次方程(a+1)x2-4x-1=0有两个不相等的实数根,则a的取值范围是 ( )
A.a>-5 B.a>-5且a≠-1 C.a<-5 D.a≥-5且a≠-1
( http: / / www.21cnjy.com )
例4. (南通)设α、β是一元二次方程x2+3x-7=0的两个根,则α2+4α+β=
( http: / / www.21cnjy.com )
例5. (北京)已知关于x的方程mx2-(m+2)x+2=0(m≠0).
(1)求证:方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
例6. (沈阳)某公司今年销售一种产品 ( http: / / www.21cnjy.com ),1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.
答案:设这个增长率为x.
依题意得: 20(1+x)2—20(1+x)=4.8
( http: / / www.21cnjy.com )
例7. (襄阳) 为响应市委市政府 ( http: / / www.21cnjy.com )提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图8所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
( http: / / www.21cnjy.com )
图8
( http: / / www.21cnjy.com )
例8. 某水果批发商经销一种高档水 ( http: / / www.21cnjy.com )果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(Ⅰ)设每千克应涨价x元,根据问题中的数量关系,用含x的代数式填表:
( http: / / www.21cnjy.com )
(Ⅱ)列出方程,并求问题的解.
( http: / / www.21cnjy.com )
巩固训练
1. 方程x(x+1)= x+1的解是( )
A.1 B.0 C.-1或0 D.1或-1
2. (聊城)用配方法解一元二次方程式ax2+bx+c=0(a≠0),此方程可变形为( )
A. B.
C. D.
3(荆州)已知α是一元二次方程x2-x-1=0较大的根,则下面对α的估计正确的是( )
A.0<α<1 B.1<α<1.5 C.1.5<α<2 D.2<α<3
4(攀枝花)若方程x2+x-1=0的两实根为α、β,那么下列说法不正确的是( )
A.α+β=-1 B.αβ=-1 C.α2+β2=3 D.+=-1
5. (天津)要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据时间和场地等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请个队参赛,则满足的关系式为( )
A. B. C. D.
6. (抚州) 关于x的一元二次方程x2-5x+k=0有两个不相等的实数根,则k可能的最大整数为 .
7. (内江)若关于x的一元二次方程(k-1) x 2+2x-2=0有不相等实数根,则k的取值范围是( )
A.k> B.k≥ C.k>且k≠1 D.k≥且k≠1
8. (丽水)如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的
通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面
积都为78,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程________.
SHAPE \* MERGEFORMAT HYPERLINK "http://www.21cnjy.com"
9. 用适当的方法解下列方程
(1)3x(x – 2)=2(2 – x) (2) x2 – 6x+8=0.
(3) 2x2 – 4x+1=0. (4) (x - 1) (x+2) = 1
10. (株洲)已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
11. (山西)某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?
( http: / / www.21cnjy.com )
12.(朝阳)长城汽车销售公司5月份销售某型 ( http: / / www.21cnjy.com )号汽车.当月该型号汽车的进价为30万元/辆,若当月销售辆超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x正为整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需要售出多少辆汽车?(注:销售利润=销售价-进价)
中考预测
1. 一元二次方程x2+px-2=0的一个根为2,则p的值为( )
A.1 B.2 C.-1 D.-2
2. 下列关于x的方程有实数根的是 ( )
A. x2-x+1=0 B. x2+x+1=0
C. (x-1)(x+2)=0 D. (x-1)2+1=0
3. 一元二次方程x2-2x+m=0有两个实数根,则m应满足的条件是( )
A.m>1 B.m=1 C.m<1 D.m≤1
4. x1,x2是一二次方程3(x-1)2=15的两个解,且x1<x2,下列说法正确的是( )
A.x1小于-1,x2大于3 B.x1小于-2,x2大于3
C.x1,x2 在-1和3之间 D.x1,x2都小于3
5. 若关于x的方程m(x ( http: / / www.21cnjy.com )+h)2+k=0(m、h、k均为常数,m≠0)的解是x1=-3,x2=2,则方程m(x+h-3)2+k=0的解 ( )
A.x1=-6,x2=-1 B.x1=0,x2=5
C.x1=-3,x2=5 D.x1=-6,x2=2
6. 某种花卉每盆的盈利与每盆的株数有一定的关系. 每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元. 要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植株,则可以列出的方程是( )
A. B.
C. D.
7. 对于实数a,b,我们定义一种运算“※”为:a※b=a2-ab,例如1※3=12-1×3.若x※4=0,则x=_________
8. 等腰三角形一条边的边长为3,它的另两条边的边长是关于x的一元二次方程x2-12x+k=0的两个根,则k的值是 .
9. 已知m、n是方程x2 –x–1=0的两实数根,则的值为 .
10. 已知关于x的方程
(1)若该方程的一个根为1,求a的值及该方程的另一根
(2)求证:不论a取何实数,该方程都有两个不相等的实数根
11. (新疆乌鲁木齐) ( http: / / www.21cnjy.com )某工厂使用旧设备生产,每月生产收入是90万元,每月另需支付设备维护费5万元;从今年1月份起使用新设备,生产收入提高且无设备维护费,使用当月生产收入达100万元,1至3月份生产收入以相同的百分率逐月增长,累计达364万元,3月份后,每月生产收入稳定在月份的水平.
⑴求使用新设备后,2月、3月生产收入的月增长率;
⑵购进新设备需一次性支付640万元,使 ( http: / / www.21cnjy.com )用新设备几个月后,该厂所得累计利润不低于使用旧设备的累计利润?(累计利润是指累计生产收入减去旧设备维护费或新设备购进费)
12. 某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.5米的正方形ABCD.点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,则中间的阴影部分组成正方形EFGH.已知烧制该种地砖平均每块需加工费0.35元,若要CE长大于0.1米,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则CE长应为多少米?
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )(2)∵方程有两个相等的实数根,
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
中考预测
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
∴x1=0.2,x2=0.05(不合题意舍去).答:CE的长应为0.2m.
同课章节目录
