人教版九年级上册数学22.3实际问题与二次函数(拱桥问题)课时训练(含简单答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数(拱桥问题)课时训练(含简单答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 974.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览

文档简介
人教版九年级上册数学22.3 实际问题与二次函数(拱桥问题)课时训练
一、单选题
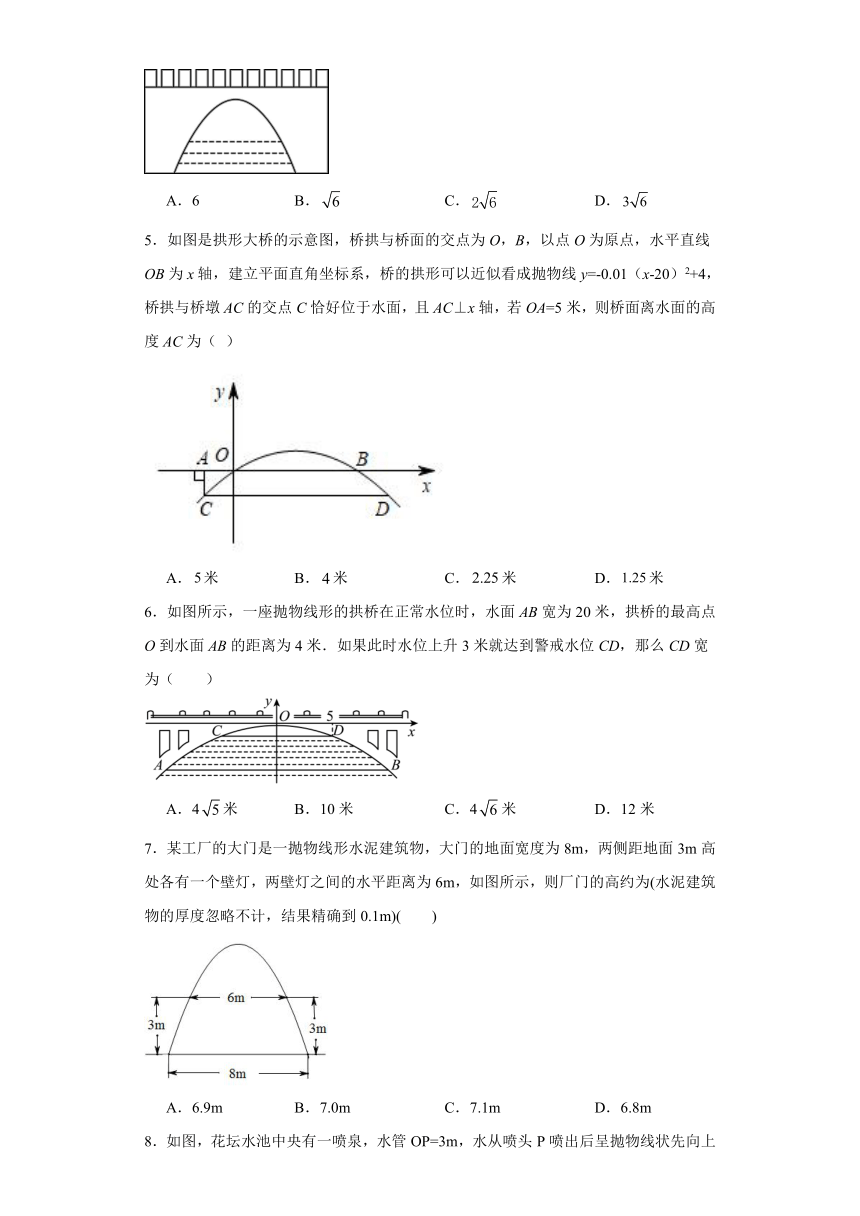
1.一座拱桥的轮廓是抛物线型(如图所示),桥高为8米,拱高6米,跨度20米.相邻两支柱间的距离均为5米,则支柱的高度为( )米.
A.米 B.3米 C.米 D.4米
2.如图,有一个截面边缘为抛物线型的水泥门洞.门洞内的地面宽度为,两侧距地面高处各有一盏灯,两灯间的水平距离为,则这个门洞内部顶端离地面的距离为( )
A. B.8 C. D.
3.廊桥是我国古老的文化遗产,如图是某座下方为抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离是( )
A.米 B.10米 C.米 D.米
4.如图所示,是一座抛物线型的拱桥,当桥下水面宽度是时,拱顶到水面的距离是,当水面下降后,水面的宽度是( )m.
A.6 B. C. D.
5.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
6.如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( )
A.4米 B.10米 C.4米 D.12米
7.某工厂的大门是一抛物线形水泥建筑物,大门的地面宽度为8m,两侧距地面3m高处各有一个壁灯,两壁灯之间的水平距离为6m,如图所示,则厂门的高约为(水泥建筑物的厚度忽略不计,结果精确到0.1m)( )
A.6.9m B.7.0m C.7.1m D.6.8m
8.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1 B.1.5
C.2 D.3
二、填空题
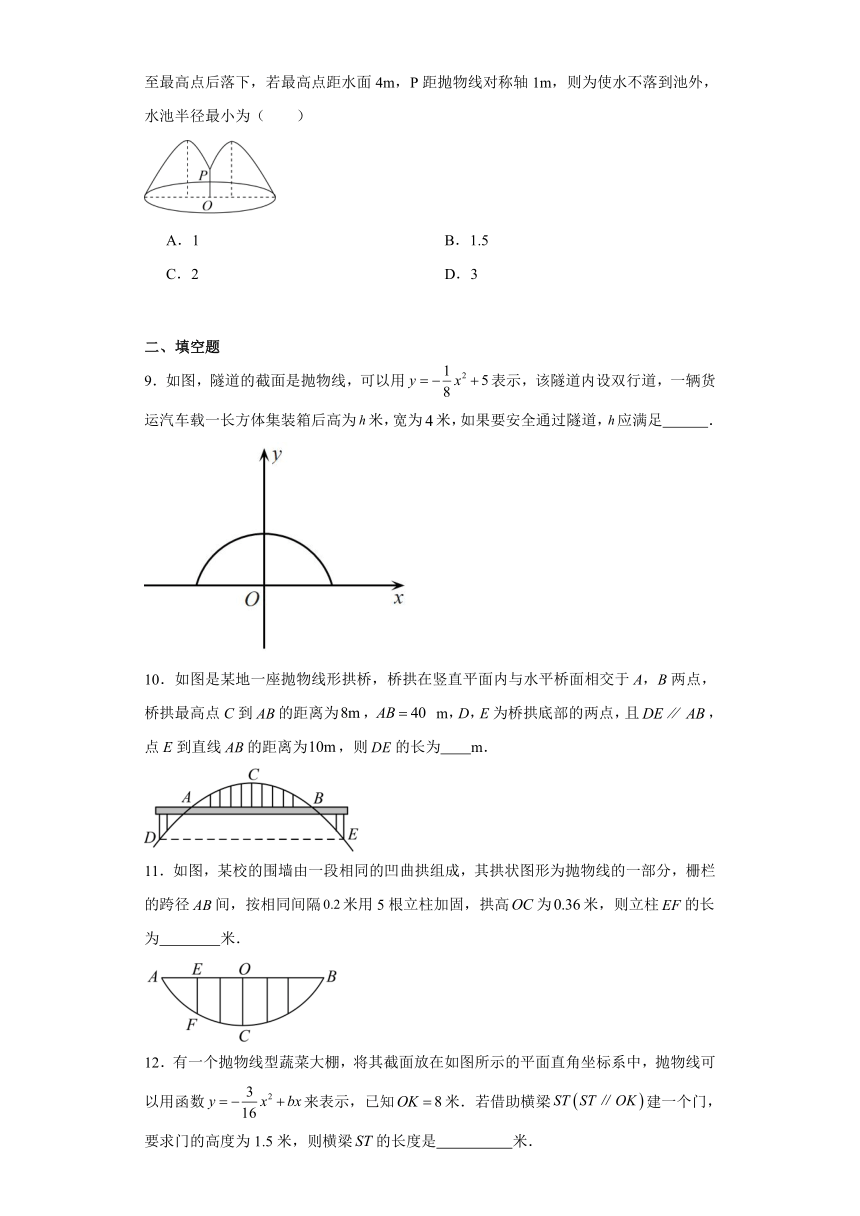
9.如图,隧道的截面是抛物线,可以用表示,该隧道内设双行道,一辆货运汽车载一长方体集装箱后高为米,宽为米,如果要安全通过隧道,应满足 .
10.如图是某地一座抛物线形拱桥,桥拱在竖直平面内与水平桥面相交于A,B两点,桥拱最高点C到的距离为, m,D,E为桥拱底部的两点,且,点E到直线的距离为,则的长为 m.
11.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径间,按相同间隔米用5根立柱加固,拱高为米,则立柱的长为 米.
12.有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数来表示,已知米.若借助横梁建一个门,要求门的高度为1.5米,则横梁的长度是 米.
13.如图是抛物线型拱桥截面,当拱顶离水面4时,水面宽6.若水面上升1,则水面宽度为 .
14.如图,有一个抛物线形拱桥,其最大高度为16m,跨度为40m,现把它的示意图放在平面直角坐标系中如图,求抛物线的解析式是
15.如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为 米
16.如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段上离中心处5米的地方,桥的高度是 米.
三、解答题
17.某公园有一个抛物线形状的观景拱桥,其横截面如图所示,在图中建立的直角坐标系(以中点为原点,抛物线对称轴所在直线为轴)中,拱桥高度,跨度.
(1)求拋物线的解析式;
(2)拱桥下,有一加固桥身的“脚手架”矩形(,在抛物线上,且点在点的左边),已知搭建“脚手架”的三边所用钢材长度为(在地面上,无需使用锎材),求“脚手架”打桩点与拱桥端点的距离.
18.如图是一座抛物线形拱桥,上面有一点P的坐标为,当水位线在位置时,A到B的水面宽,求此时水位线离桥顶的高度h.
19.根据《平顶山市志》记载,中兴路湛河桥是“市区第一座横跨湛河的大桥”.已知该桥的桥拱为抛物线形,在正常水位时测得水面的宽为,最高点距离水面,如图所示以所在的直线为轴,的中点为原点建立平面直角坐标系.
(1)求该抛物线的表达式;
(2)某次大雨后水面上涨至,测得最高点距离的高度为,求桥拱下水面的宽度.
20.一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点位于的中央且距地面6m,建立如图所示的坐标系.
(1)求抛物线的表达式;
(2)该隧道内设双行道,中间隔离带1m,一辆货车高4m,宽m,能否安全通过,为什么?
参考答案:
1.C
2.D
3.A
4.C
5.C
6.B
7.A
8.D
9.
10.60
11./
12.
13.
14.
15.0.64
16.15
17.(1)
(2)4m
18.
19.(1)
(2)桥拱下水面的宽度为
20.(1)
(2)不能;
答案第2页,共2页
一、单选题
1.一座拱桥的轮廓是抛物线型(如图所示),桥高为8米,拱高6米,跨度20米.相邻两支柱间的距离均为5米,则支柱的高度为( )米.
A.米 B.3米 C.米 D.4米
2.如图,有一个截面边缘为抛物线型的水泥门洞.门洞内的地面宽度为,两侧距地面高处各有一盏灯,两灯间的水平距离为,则这个门洞内部顶端离地面的距离为( )
A. B.8 C. D.
3.廊桥是我国古老的文化遗产,如图是某座下方为抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离是( )
A.米 B.10米 C.米 D.米
4.如图所示,是一座抛物线型的拱桥,当桥下水面宽度是时,拱顶到水面的距离是,当水面下降后,水面的宽度是( )m.
A.6 B. C. D.
5.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-0.01(x-20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )
A.米 B.米 C.米 D.米
6.如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( )
A.4米 B.10米 C.4米 D.12米
7.某工厂的大门是一抛物线形水泥建筑物,大门的地面宽度为8m,两侧距地面3m高处各有一个壁灯,两壁灯之间的水平距离为6m,如图所示,则厂门的高约为(水泥建筑物的厚度忽略不计,结果精确到0.1m)( )
A.6.9m B.7.0m C.7.1m D.6.8m
8.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1 B.1.5
C.2 D.3
二、填空题
9.如图,隧道的截面是抛物线,可以用表示,该隧道内设双行道,一辆货运汽车载一长方体集装箱后高为米,宽为米,如果要安全通过隧道,应满足 .
10.如图是某地一座抛物线形拱桥,桥拱在竖直平面内与水平桥面相交于A,B两点,桥拱最高点C到的距离为, m,D,E为桥拱底部的两点,且,点E到直线的距离为,则的长为 m.
11.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径间,按相同间隔米用5根立柱加固,拱高为米,则立柱的长为 米.
12.有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数来表示,已知米.若借助横梁建一个门,要求门的高度为1.5米,则横梁的长度是 米.
13.如图是抛物线型拱桥截面,当拱顶离水面4时,水面宽6.若水面上升1,则水面宽度为 .
14.如图,有一个抛物线形拱桥,其最大高度为16m,跨度为40m,现把它的示意图放在平面直角坐标系中如图,求抛物线的解析式是
15.如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为 米
16.如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段上离中心处5米的地方,桥的高度是 米.
三、解答题
17.某公园有一个抛物线形状的观景拱桥,其横截面如图所示,在图中建立的直角坐标系(以中点为原点,抛物线对称轴所在直线为轴)中,拱桥高度,跨度.
(1)求拋物线的解析式;
(2)拱桥下,有一加固桥身的“脚手架”矩形(,在抛物线上,且点在点的左边),已知搭建“脚手架”的三边所用钢材长度为(在地面上,无需使用锎材),求“脚手架”打桩点与拱桥端点的距离.
18.如图是一座抛物线形拱桥,上面有一点P的坐标为,当水位线在位置时,A到B的水面宽,求此时水位线离桥顶的高度h.
19.根据《平顶山市志》记载,中兴路湛河桥是“市区第一座横跨湛河的大桥”.已知该桥的桥拱为抛物线形,在正常水位时测得水面的宽为,最高点距离水面,如图所示以所在的直线为轴,的中点为原点建立平面直角坐标系.
(1)求该抛物线的表达式;
(2)某次大雨后水面上涨至,测得最高点距离的高度为,求桥拱下水面的宽度.
20.一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点位于的中央且距地面6m,建立如图所示的坐标系.
(1)求抛物线的表达式;
(2)该隧道内设双行道,中间隔离带1m,一辆货车高4m,宽m,能否安全通过,为什么?
参考答案:
1.C
2.D
3.A
4.C
5.C
6.B
7.A
8.D
9.
10.60
11./
12.
13.
14.
15.0.64
16.15
17.(1)
(2)4m
18.
19.(1)
(2)桥拱下水面的宽度为
20.(1)
(2)不能;
答案第2页,共2页
同课章节目录
