人教A版(2019)选择性必修第二册 4.2.1 等差数列的概念 课件(共25张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册 4.2.1 等差数列的概念 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 02:11:38 | ||
图片预览








文档简介
(共25张PPT)
4.2.1 等差数列的概念
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
(1)1682,1758,1834,1910,1986,( )
你能预测出下一次的大致时间吗?
2062
主持人问: 最近的时间什么时候可以看到哈雷慧星?
天文学家陈丹说: 2062年左右。
相差76
课题引入
你能根据规律在( )内填上合适的数吗?
(3) 1,4,7,10,( ),16,…
(4) 2, 0, -2, -4, -6,( )…
(1)1682,1758,1834,1910,1986,(2062).
( 2 ) 32, 25.5, 19, 12.5, 6, ( ),-7
13
-8
课题引入
-0.5
观察下面几个数列有什么特点,
并写出它的通项公式:
通过相连两项之间的运算发现
哪些有趣的规律?
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差用d表示.
等差数列的定义:
它们是等差数列吗?
(2) 5,5,5,5,5,5,…
公差 d=0 常数列
公差 d= 2x
(1) 1, 3, 5, 7, 9, 2, 4, 6, 8, 10
×
(3)
等差数列定义
……
……
+)
公式推导
等差数列的通项公式:
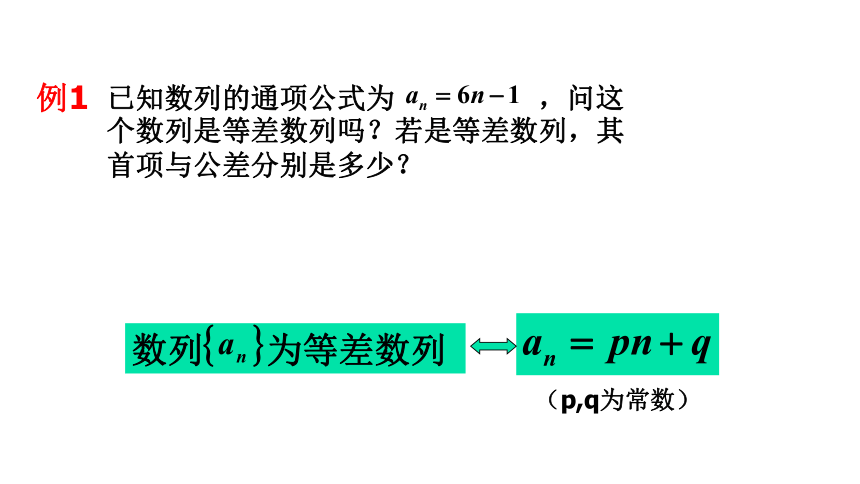
例1
已知数列的通项公式为 ,问这个数列是等差数列吗?若是等差数列,其首项与公差分别是多少?
数列 为等差数列
(p,q为常数)
等差数列通项公式
等差数列的判定和证明
例3
(1)求等差数列8,5,2,…的第20项;
(2)等差数列-5,-9,-13,…的第几项是-401?
(3)等差数列-5,-9,-13,…,-321的项数?
例4
等差数列 中,已知
(1)求
(2)判断数列的单调性;
(3)若 ,求 n的最小值;
等差数列的单调性:
如果等差数列 {an}的首项是a1,
公差是d,那么
d>0时,数列为递增数列;
d<0时,数列为递减数列;
d=0时,数列为常数数列
例6:
等差数列的对称设法
等差中项
等差中项的应用探究二等差数列的性质
例3:
等差数列性质的应用
探究三
例4:
课堂小结
道可道,明白就好!
4.2.1 等差数列的概念
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
(1)1682,1758,1834,1910,1986,( )
你能预测出下一次的大致时间吗?
2062
主持人问: 最近的时间什么时候可以看到哈雷慧星?
天文学家陈丹说: 2062年左右。
相差76
课题引入
你能根据规律在( )内填上合适的数吗?
(3) 1,4,7,10,( ),16,…
(4) 2, 0, -2, -4, -6,( )…
(1)1682,1758,1834,1910,1986,(2062).
( 2 ) 32, 25.5, 19, 12.5, 6, ( ),-7
13
-8
课题引入
-0.5
观察下面几个数列有什么特点,
并写出它的通项公式:
通过相连两项之间的运算发现
哪些有趣的规律?
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差用d表示.
等差数列的定义:
它们是等差数列吗?
(2) 5,5,5,5,5,5,…
公差 d=0 常数列
公差 d= 2x
(1) 1, 3, 5, 7, 9, 2, 4, 6, 8, 10
×
(3)
等差数列定义
……
……
+)
公式推导
等差数列的通项公式:
例1
已知数列的通项公式为 ,问这个数列是等差数列吗?若是等差数列,其首项与公差分别是多少?
数列 为等差数列
(p,q为常数)
等差数列通项公式
等差数列的判定和证明
例3
(1)求等差数列8,5,2,…的第20项;
(2)等差数列-5,-9,-13,…的第几项是-401?
(3)等差数列-5,-9,-13,…,-321的项数?
例4
等差数列 中,已知
(1)求
(2)判断数列的单调性;
(3)若 ,求 n的最小值;
等差数列的单调性:
如果等差数列 {an}的首项是a1,
公差是d,那么
d>0时,数列为递增数列;
d<0时,数列为递减数列;
d=0时,数列为常数数列
例6:
等差数列的对称设法
等差中项
等差中项的应用探究二等差数列的性质
例3:
等差数列性质的应用
探究三
例4:
课堂小结
道可道,明白就好!
