人教版数学九年级上册 23.2.3关于原点对称的点的坐标(第3课时) 课件(共12张PPT)
文档属性
| 名称 | 人教版数学九年级上册 23.2.3关于原点对称的点的坐标(第3课时) 课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 08:27:21 | ||
图片预览





文档简介
(共12张PPT)
第二十三章 旋转
23.2 中心对称
第 3 课时
问题1 (1)什么是中心对称?什么是中心对称图形?中心对称有什么性质?
(2)点P(x,y)关于 y 轴对称的点的坐标 P ′ ( , );
(3)点P(x,y)关于 x 轴对称的点的坐标P ′ ( , ).
归纳:
(1)如果把一个图形关于某一点旋转180°后能够与另一个图形重合,那么就说这两个图形成中心对称;把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原图形重合,那么就说这个图形是中心对称图形.
(2)点P(x,y)关于y轴对称的点的坐标 P ′ ( -x , y );
(3)点P(x,y)关于x轴对称的点的坐标P ′ ( x , -y ).
一、提出问题,思考引入
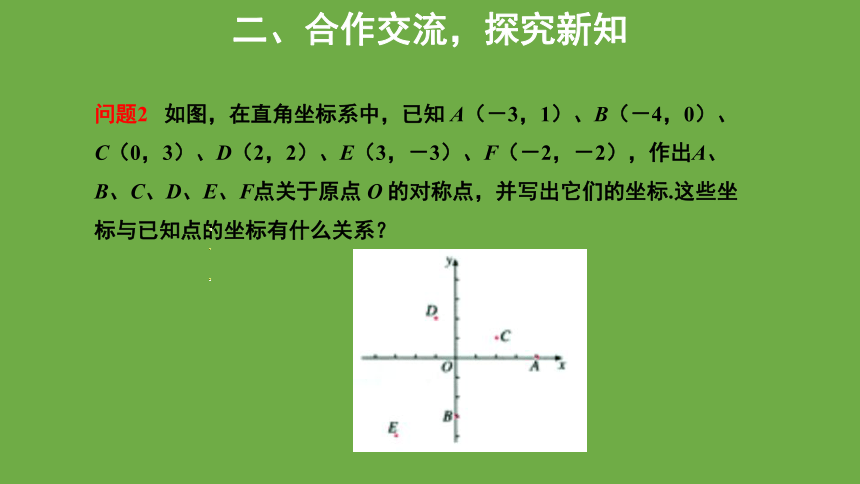
问题2 如图,在直角坐标系中,已知 A(-3,1)、B(-4,0)、C(0,3)、D(2,2)、E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点 O 的对称点,并写出它们的坐标.这些坐标与已知点的坐标有什么关系?
二、合作交流,探究新知
画法:(1)连结 AO 并延长 AO,
(2)在射线 AO 上截取 OA′=OA,
(3)过 A 作 AD′⊥x 轴于 D′点,过 A′ 作A′D″⊥x 轴于点 D″.
∵△AD′O 与△A′D″O 全等.
∴AD′=A′D″,OA=OA′.∴A′(3,-1).
同理可得B、C、D、E、F 这些点关于原点的中心对称点的坐标.
二、合作交流,探究新知
追问1:关于原点作中心对称时,它们的横坐标与横坐标绝对值什么关系?
追问2:纵坐标与纵坐标的绝对值又有什么关系?
追问3:坐标与坐标之间符号又有什么特点?
归纳:从上可知,横坐标与横坐标的绝对值相等,纵坐标与纵坐标的绝对值相等.坐标符号相反,即点 P(x,y) 关于原点的对称点为 P′(-x,-y).
结论:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为 P′(-x,-y).
二、合作交流,探究新知
例1 如左图所示,利用关于原点对称的点的坐标的关系,作出与△ABC 关于原点对称的图形.
解:点P(x,y) 关于原点的对称点为P′(-x,-y),因此△ABC 的三个顶点A(-4,1),B(-1,-1),C(-3,2)关于原点的对称点分别为A′(4,-1),B′(1,1),C′(3,-2),依次连接A′B′,B′C′,C′A′,就可得到与△ABC 关于原点对称的△A′B′C′(右图).
三、运用新知
例2 已知△ABC,A(1,2),B(-1,3),C(-2,4)利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
分析:先在直角坐标系中画出A、B、C 三点并连结组成△ABC,要作出△ABC 关于原点 O 的对称三角形,只需作出△ABC 中的A、B、C 三点关于原点的对称点,依次连结,便可得到所求作的△A′B′C′.
三、运用新知
1. 如图,点A,B,C 的坐标分别为(0,﹣1),(0,2),(3,0).从下面四个点M(3,3),N(3,﹣3),P(﹣3,0),Q(﹣3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A. M B. N C. P D. Q
解:根据平行四边形的判定,可知A、B、P都能够和已知的三个点组成平行四边形,则一定是中心对称图形.所以选择 C.
四、巩固新知
2. (1)点A(2,-3)关于原点对称的点的坐标A′( , );
(2)点B(5,7)关于原点对称的点的坐标B′( , );
(3)点C(-8,-1)关于原点对称的点的坐标C′( , ).
解:A′(-2,3 );B′( -5 ,- 7);C′( 8,1).
3. 下列各点中哪两个点关于原点对称?
A(-5,0)、B(0,2)、C(2,-1)、D(2,0)、E(0,5)、 F(-2,1)、G (-2,-1).
解:C(2,-1)与 F(-2,1)关于原点对称.
四、巩固新知
4. 已知点 A(a,1) 和点 A′(5,b) 是关于原点 O 的对称点,求 a + b 的值.
解:∵点 A(a,1) 和点 A′(5,b) 是关于原点 O 的对称点,
∴a=-5,b=-1,∴a + b =-5 +(-1)= -6.
5. 若点 P(-1 - 2a,2a - 4)关于原点对称的点是第一象限的点,则 a 整数解有多少个?
解:∵点P(-1 - 2a,2a - 4)关于原点对称点的坐标是(1 + 2a,4 - 2a),且这个点是第一象限内的点,∴1 + 2a > 0,4 - 2a > 0,解得-0.5< a <2,∴a 整数解有 2 个.
四、巩固新知
回顾本节内容,并请学生回答下列问题:
本节课学习了哪些主要内容?
2. 本节课你有什么收获和体会?
3. 对本节课所学知识你还有哪些疑惑?
本节课应掌握:两个点关于原点对称时,它们的坐标符号相反,
即点 P(x,y) 关于原点的对称点为 P′(-x,-y).
利用关于原点对称的点的坐标变化规律解决一些实际问题.
五、归纳小结
再 见
第二十三章 旋转
23.2 中心对称
第 3 课时
问题1 (1)什么是中心对称?什么是中心对称图形?中心对称有什么性质?
(2)点P(x,y)关于 y 轴对称的点的坐标 P ′ ( , );
(3)点P(x,y)关于 x 轴对称的点的坐标P ′ ( , ).
归纳:
(1)如果把一个图形关于某一点旋转180°后能够与另一个图形重合,那么就说这两个图形成中心对称;把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原图形重合,那么就说这个图形是中心对称图形.
(2)点P(x,y)关于y轴对称的点的坐标 P ′ ( -x , y );
(3)点P(x,y)关于x轴对称的点的坐标P ′ ( x , -y ).
一、提出问题,思考引入
问题2 如图,在直角坐标系中,已知 A(-3,1)、B(-4,0)、C(0,3)、D(2,2)、E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点 O 的对称点,并写出它们的坐标.这些坐标与已知点的坐标有什么关系?
二、合作交流,探究新知
画法:(1)连结 AO 并延长 AO,
(2)在射线 AO 上截取 OA′=OA,
(3)过 A 作 AD′⊥x 轴于 D′点,过 A′ 作A′D″⊥x 轴于点 D″.
∵△AD′O 与△A′D″O 全等.
∴AD′=A′D″,OA=OA′.∴A′(3,-1).
同理可得B、C、D、E、F 这些点关于原点的中心对称点的坐标.
二、合作交流,探究新知
追问1:关于原点作中心对称时,它们的横坐标与横坐标绝对值什么关系?
追问2:纵坐标与纵坐标的绝对值又有什么关系?
追问3:坐标与坐标之间符号又有什么特点?
归纳:从上可知,横坐标与横坐标的绝对值相等,纵坐标与纵坐标的绝对值相等.坐标符号相反,即点 P(x,y) 关于原点的对称点为 P′(-x,-y).
结论:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为 P′(-x,-y).
二、合作交流,探究新知
例1 如左图所示,利用关于原点对称的点的坐标的关系,作出与△ABC 关于原点对称的图形.
解:点P(x,y) 关于原点的对称点为P′(-x,-y),因此△ABC 的三个顶点A(-4,1),B(-1,-1),C(-3,2)关于原点的对称点分别为A′(4,-1),B′(1,1),C′(3,-2),依次连接A′B′,B′C′,C′A′,就可得到与△ABC 关于原点对称的△A′B′C′(右图).
三、运用新知
例2 已知△ABC,A(1,2),B(-1,3),C(-2,4)利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
分析:先在直角坐标系中画出A、B、C 三点并连结组成△ABC,要作出△ABC 关于原点 O 的对称三角形,只需作出△ABC 中的A、B、C 三点关于原点的对称点,依次连结,便可得到所求作的△A′B′C′.
三、运用新知
1. 如图,点A,B,C 的坐标分别为(0,﹣1),(0,2),(3,0).从下面四个点M(3,3),N(3,﹣3),P(﹣3,0),Q(﹣3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A. M B. N C. P D. Q
解:根据平行四边形的判定,可知A、B、P都能够和已知的三个点组成平行四边形,则一定是中心对称图形.所以选择 C.
四、巩固新知
2. (1)点A(2,-3)关于原点对称的点的坐标A′( , );
(2)点B(5,7)关于原点对称的点的坐标B′( , );
(3)点C(-8,-1)关于原点对称的点的坐标C′( , ).
解:A′(-2,3 );B′( -5 ,- 7);C′( 8,1).
3. 下列各点中哪两个点关于原点对称?
A(-5,0)、B(0,2)、C(2,-1)、D(2,0)、E(0,5)、 F(-2,1)、G (-2,-1).
解:C(2,-1)与 F(-2,1)关于原点对称.
四、巩固新知
4. 已知点 A(a,1) 和点 A′(5,b) 是关于原点 O 的对称点,求 a + b 的值.
解:∵点 A(a,1) 和点 A′(5,b) 是关于原点 O 的对称点,
∴a=-5,b=-1,∴a + b =-5 +(-1)= -6.
5. 若点 P(-1 - 2a,2a - 4)关于原点对称的点是第一象限的点,则 a 整数解有多少个?
解:∵点P(-1 - 2a,2a - 4)关于原点对称点的坐标是(1 + 2a,4 - 2a),且这个点是第一象限内的点,∴1 + 2a > 0,4 - 2a > 0,解得-0.5< a <2,∴a 整数解有 2 个.
四、巩固新知
回顾本节内容,并请学生回答下列问题:
本节课学习了哪些主要内容?
2. 本节课你有什么收获和体会?
3. 对本节课所学知识你还有哪些疑惑?
本节课应掌握:两个点关于原点对称时,它们的坐标符号相反,
即点 P(x,y) 关于原点的对称点为 P′(-x,-y).
利用关于原点对称的点的坐标变化规律解决一些实际问题.
五、归纳小结
再 见
同课章节目录
