人教版数学九年级上册 22.3实际问题与二次函数(第1课时) 课件(共14张PPT)
文档属性
| 名称 | 人教版数学九年级上册 22.3实际问题与二次函数(第1课时) 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 213.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第二十二章 二次函数
22.3 实际问题与二次函数
第 1 课时
一、学习目标
1.学会求二次函数y=ax2+bx+c的最小(大)值.
2.能够从实际问题中抽象出二次函数关系,并运用二次函数及性质解决最小(大)值等实际问题.
从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是h= 30t -5t 2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
二、创设情境,揭示课题
二、创设情境,揭示课题
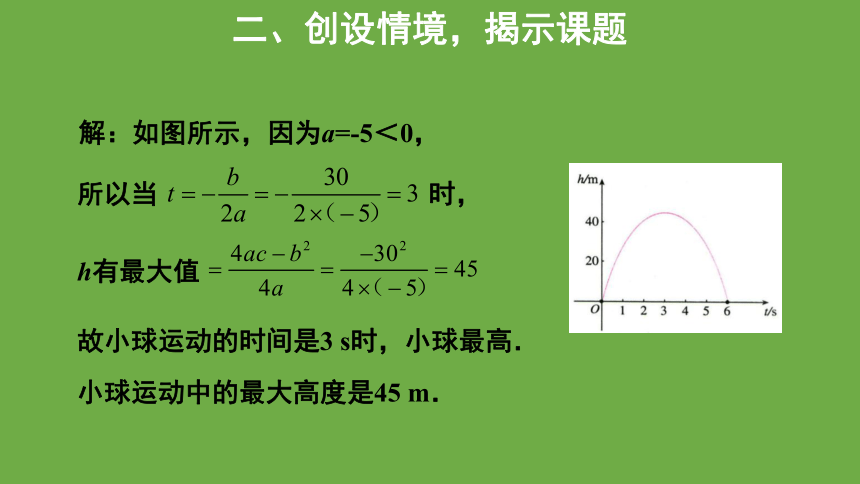
故小球运动的时间是3 s时,小球最高.
小球运动中的最大高度是45 m.
所以当 时,
解:如图所示,因为a=-5<0,
h有最大值
如何求出二次函数 y = ax2 + bx + c 的最小值和最大值?
三、合作探究,形成新知
一般地,当a>0时,抛物线 y = ax2 + bx + c 的顶点是最低点,
当 时,二次函数 y = ax2 + bx + c 有最小值 ;
当a<0时,抛物线 y = ax2 + bx + c 的顶点是最高点,
当 时,二次函数 y = ax2 + bx + c 有最大值 。
例 用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形
一边长 l 的变化而变化.当 l 是多少米时,场地的面积 S 最大?
四、例题分析,深化提高
S 有最大值为
答:当 l 是 15 m 时,场地的面积 S 最大.
整理,得
(0<l<30),
因此,当 时,
解:依题意,得 ,
四、例题分析,深化提高
四、例题分析,深化提高
解决二次函数最值问题的一般步骤:
(1)列出二次函数的解析式,并根据自变量的实际
意义,确定自变量的取值范围;
(2)在自变量的取值范围内,求出二次函数的最大
值或最小值.
1.军事演坦的草原上进行,一门迫击炮发射的一发炮
弹飞行的高度y(m)与飞行时间x(s)的关系满足y=x2+10x,
经过______s,炮弹到达它的最高点,最高点的高度是_____m,经过______s,炮弹落到地上爆炸.
2.已知一个直角三角形两直角边之和为20 cm,则这个直角
三角形的最大面积为( )
A.25 cm2 B.50 cm2 C.100 cm2 D.不确定
25
B
125
50
五、练习巩固,综合应用
解:设将铁丝分成长为x cm,(120-x )cm的两段,并分别围成
正方形,则正方形的边长分别为 cm, cm.
设它们的面积和为y cm2,则
当x=60时,y的最小值为450.
答:它们的面积和最小为450 cm2.
五、练习巩固,综合应用
3.若把一根长为120 cm的铁丝分成两部分 ,每一部分均弯曲
成一个正方形,它们的面积和最小是多少?
4.飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是s=60t-1.5t2.
飞机着陆后滑行多远才能停下来?
600 m
五、练习巩固,综合应用
六、课堂小结
1.一般地,当a>0时,抛物线y=ax2+bx+c的顶点是最低点,也就是说,当 时,二次函数y=ax2+bx+c有最小值 ;
当a<0时,抛物线y=ax2 +bx +c的顶点是最高点,也就是说,当 时,二次函数y=ax2+bx+c有最大值
。
2.解决二次函数最值问题的一般步骤:
(1)列出二次函数的解析式,并根据自变量的实际
意义,确定自变量的取值范围;
(2)在自变量的取值范围内,求出二次函数的最大
值或最小值.
六、课堂小结
再 见
第二十二章 二次函数
22.3 实际问题与二次函数
第 1 课时
一、学习目标
1.学会求二次函数y=ax2+bx+c的最小(大)值.
2.能够从实际问题中抽象出二次函数关系,并运用二次函数及性质解决最小(大)值等实际问题.
从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是h= 30t -5t 2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
二、创设情境,揭示课题
二、创设情境,揭示课题
故小球运动的时间是3 s时,小球最高.
小球运动中的最大高度是45 m.
所以当 时,
解:如图所示,因为a=-5<0,
h有最大值
如何求出二次函数 y = ax2 + bx + c 的最小值和最大值?
三、合作探究,形成新知
一般地,当a>0时,抛物线 y = ax2 + bx + c 的顶点是最低点,
当 时,二次函数 y = ax2 + bx + c 有最小值 ;
当a<0时,抛物线 y = ax2 + bx + c 的顶点是最高点,
当 时,二次函数 y = ax2 + bx + c 有最大值 。
例 用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形
一边长 l 的变化而变化.当 l 是多少米时,场地的面积 S 最大?
四、例题分析,深化提高
S 有最大值为
答:当 l 是 15 m 时,场地的面积 S 最大.
整理,得
(0<l<30),
因此,当 时,
解:依题意,得 ,
四、例题分析,深化提高
四、例题分析,深化提高
解决二次函数最值问题的一般步骤:
(1)列出二次函数的解析式,并根据自变量的实际
意义,确定自变量的取值范围;
(2)在自变量的取值范围内,求出二次函数的最大
值或最小值.
1.军事演坦的草原上进行,一门迫击炮发射的一发炮
弹飞行的高度y(m)与飞行时间x(s)的关系满足y=x2+10x,
经过______s,炮弹到达它的最高点,最高点的高度是_____m,经过______s,炮弹落到地上爆炸.
2.已知一个直角三角形两直角边之和为20 cm,则这个直角
三角形的最大面积为( )
A.25 cm2 B.50 cm2 C.100 cm2 D.不确定
25
B
125
50
五、练习巩固,综合应用
解:设将铁丝分成长为x cm,(120-x )cm的两段,并分别围成
正方形,则正方形的边长分别为 cm, cm.
设它们的面积和为y cm2,则
当x=60时,y的最小值为450.
答:它们的面积和最小为450 cm2.
五、练习巩固,综合应用
3.若把一根长为120 cm的铁丝分成两部分 ,每一部分均弯曲
成一个正方形,它们的面积和最小是多少?
4.飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是s=60t-1.5t2.
飞机着陆后滑行多远才能停下来?
600 m
五、练习巩固,综合应用
六、课堂小结
1.一般地,当a>0时,抛物线y=ax2+bx+c的顶点是最低点,也就是说,当 时,二次函数y=ax2+bx+c有最小值 ;
当a<0时,抛物线y=ax2 +bx +c的顶点是最高点,也就是说,当 时,二次函数y=ax2+bx+c有最大值
。
2.解决二次函数最值问题的一般步骤:
(1)列出二次函数的解析式,并根据自变量的实际
意义,确定自变量的取值范围;
(2)在自变量的取值范围内,求出二次函数的最大
值或最小值.
六、课堂小结
再 见
同课章节目录
