人教版数学九年级上册 22.3实际问题与二次函数(第3课时) 课件(共12张PPT)
文档属性
| 名称 | 人教版数学九年级上册 22.3实际问题与二次函数(第3课时) 课件(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 421.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 08:39:52 | ||
图片预览



文档简介
(共12张PPT)
第二十二章 二次函数
22.3 实际问题与二次函数
第 3 课时
1.学会将实际问题转化为数学问题.
2.掌握用二次函数的知识解决有关的实际问题.
一、学习目标
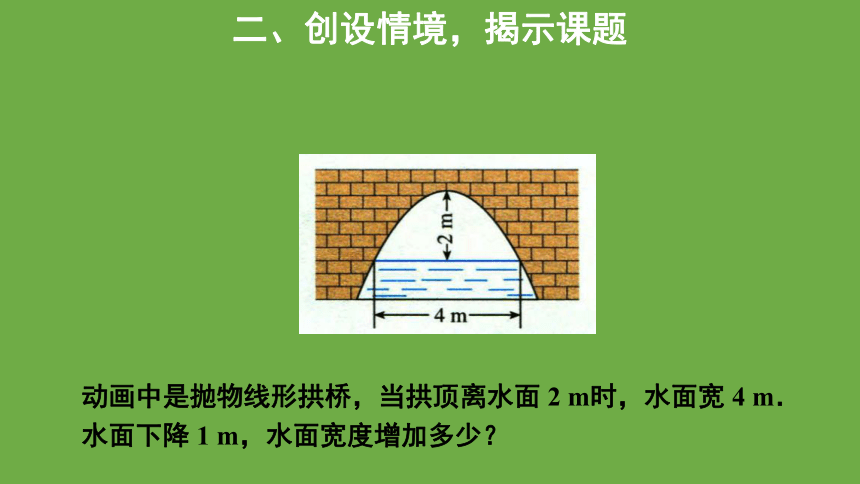
动画中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m.
水面下降 1 m,水面宽度增加多少?
二、创设情境,揭示课题
解:如图所示,设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得 -2=a×22.
解得 .
故这条抛物线表示的二次函数为 .
当水面下降1 m时,水面的纵坐标为-3,
所以 ,解得 .
所以水面宽度为 m.
所以当水面下降1 m时,水面宽度增加了 m.
三、合作探究,形成新知
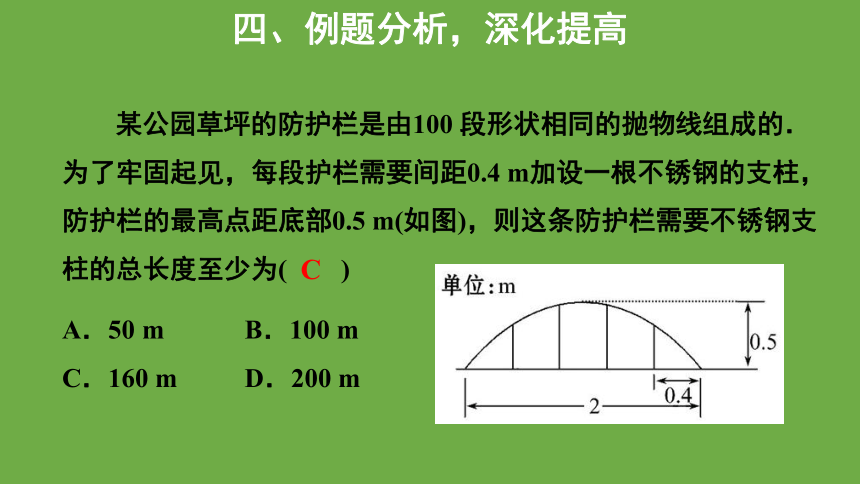
某公园草坪的防护栏是由100 段形状相同的抛物线组成的.
为了牢固起见,每段护栏需要间距0.4 m加设一根不锈钢的支柱,
防护栏的最高点距底部0.5 m(如图),则这条防护栏需要不锈钢支
柱的总长度至少为( )
A.50 m B.100 m
C.160 m D.200 m
C
四、例题分析,深化提高
四、例题分析,深化提高
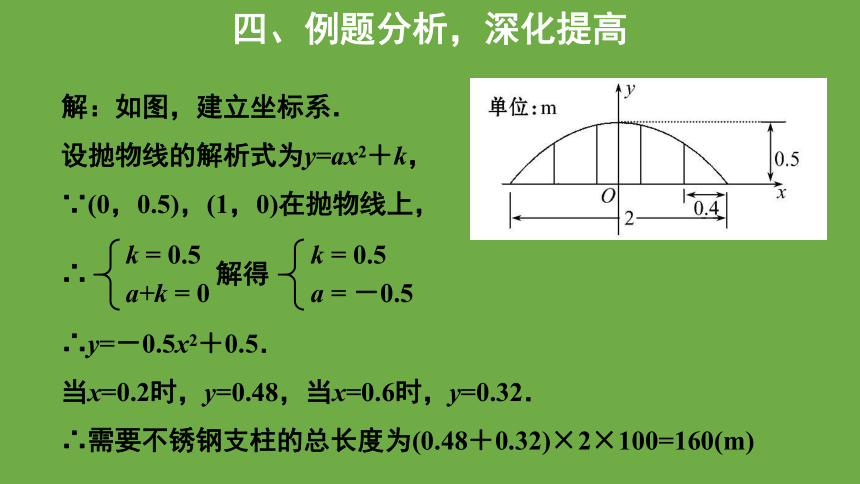
解:如图,建立坐标系.
设抛物线的解析式为y=ax2+k,
∵(0,0.5),(1,0)在抛物线上,
∴ 解得
∴y=-0.5x2+0.5.
当x=0.2时,y=0.48,当x=0.6时,y=0.32.
∴需要不锈钢支柱的总长度为(0.48+0.32)×2×100=160(m)
k = 0.5
a+k = 0
k = 0.5
a = -0.5
1.某一拱桥呈抛物线形,其函数解析式为y=-0.25x2,
当拱桥下水面宽为12 m时,水面离拱桥顶端的高度h是
( )
D
五、练习巩固,综合应用
A.3 m B. C. D.9 m
2.如图,有一座抛物线形的拱桥,桥下水面处在目前的水位时,水面宽AB=10 m.如果水位上升2 m,就将达到警戒线CD,这时水面的宽为8 m.若洪水到来,水位以每小时0.1 m的速度上升,经过多少小时会达到拱顶?
五、练习巩固,综合应用
五、练习巩固,综合应用
解:以AB所在的直线为x轴,AB的中点为原点,建立直角坐标系。
则抛物线的顶点E在y轴上,且B、D两点
的坐标分别为(5,0)、(4,2),
设抛物线的解析式为y=ax2+k;
由B、D两点在抛物线上,
得 ,解得 , ,则
所以顶点E的坐标为 ,则OE= ,
若洪水到来,水位以每小时0.1 m速度上升,经过 会达到拱顶。
16a+k=2
25a+k=0
六、课堂小结
1.一般地,当a>0时,抛物线y=ax2+bx+c的顶点是最低点,也就是说,当 时,二次函数y=ax2+bx+c有最小值 ;
当a<0时,抛物线y=ax2 +bx +c的顶点是最高点,也就是说,当 时,二次函数y=ax2+bx+c有最大值
。
2.解决二次函数最值问题的一般步骤:
(1)列出二次函数的解析式,并根据自变量的实际
意义,确定自变量的取值范围;
(2)在自变量的取值范围内,求出二次函数的最大
值或最小值.
六、课堂小结
再 见
第二十二章 二次函数
22.3 实际问题与二次函数
第 3 课时
1.学会将实际问题转化为数学问题.
2.掌握用二次函数的知识解决有关的实际问题.
一、学习目标
动画中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m.
水面下降 1 m,水面宽度增加多少?
二、创设情境,揭示课题
解:如图所示,设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得 -2=a×22.
解得 .
故这条抛物线表示的二次函数为 .
当水面下降1 m时,水面的纵坐标为-3,
所以 ,解得 .
所以水面宽度为 m.
所以当水面下降1 m时,水面宽度增加了 m.
三、合作探究,形成新知
某公园草坪的防护栏是由100 段形状相同的抛物线组成的.
为了牢固起见,每段护栏需要间距0.4 m加设一根不锈钢的支柱,
防护栏的最高点距底部0.5 m(如图),则这条防护栏需要不锈钢支
柱的总长度至少为( )
A.50 m B.100 m
C.160 m D.200 m
C
四、例题分析,深化提高
四、例题分析,深化提高
解:如图,建立坐标系.
设抛物线的解析式为y=ax2+k,
∵(0,0.5),(1,0)在抛物线上,
∴ 解得
∴y=-0.5x2+0.5.
当x=0.2时,y=0.48,当x=0.6时,y=0.32.
∴需要不锈钢支柱的总长度为(0.48+0.32)×2×100=160(m)
k = 0.5
a+k = 0
k = 0.5
a = -0.5
1.某一拱桥呈抛物线形,其函数解析式为y=-0.25x2,
当拱桥下水面宽为12 m时,水面离拱桥顶端的高度h是
( )
D
五、练习巩固,综合应用
A.3 m B. C. D.9 m
2.如图,有一座抛物线形的拱桥,桥下水面处在目前的水位时,水面宽AB=10 m.如果水位上升2 m,就将达到警戒线CD,这时水面的宽为8 m.若洪水到来,水位以每小时0.1 m的速度上升,经过多少小时会达到拱顶?
五、练习巩固,综合应用
五、练习巩固,综合应用
解:以AB所在的直线为x轴,AB的中点为原点,建立直角坐标系。
则抛物线的顶点E在y轴上,且B、D两点
的坐标分别为(5,0)、(4,2),
设抛物线的解析式为y=ax2+k;
由B、D两点在抛物线上,
得 ,解得 , ,则
所以顶点E的坐标为 ,则OE= ,
若洪水到来,水位以每小时0.1 m速度上升,经过 会达到拱顶。
16a+k=2
25a+k=0
六、课堂小结
1.一般地,当a>0时,抛物线y=ax2+bx+c的顶点是最低点,也就是说,当 时,二次函数y=ax2+bx+c有最小值 ;
当a<0时,抛物线y=ax2 +bx +c的顶点是最高点,也就是说,当 时,二次函数y=ax2+bx+c有最大值
。
2.解决二次函数最值问题的一般步骤:
(1)列出二次函数的解析式,并根据自变量的实际
意义,确定自变量的取值范围;
(2)在自变量的取值范围内,求出二次函数的最大
值或最小值.
六、课堂小结
再 见
同课章节目录
