人教版数学九年级上册 24.2实验与探究 圆和圆的位置关系(第3课时)课件(共24张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.2实验与探究 圆和圆的位置关系(第3课时)课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 948.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 08:42:27 | ||
图片预览








文档简介
(共24张PPT)
第二十四章 圆
24.2 实验与探究
圆和圆的位置关系
1. 点与圆的位置关系
2. 直线与圆的位置关系
3. 两个圆的位置关系如何呢?这就是我们这节课要解决的问题
一、复习回顾
关系
点在圆内
点在圆上
点在圆外
数量特征
dd=r
d>r
点和圆的三种位置关系
一、复习回顾
直线与圆的位置关系
公共点数目
公共点名称
直线名称
数量特征
直线和圆的三种位置关系
相交 相切 相离
2 1 0
交点 切点 无
割线 切线 无
d r
一、复习回顾
(一)观察
请认真观察两圆的运动过程,注意两圆的位置关系
二、合作交流,探究新知
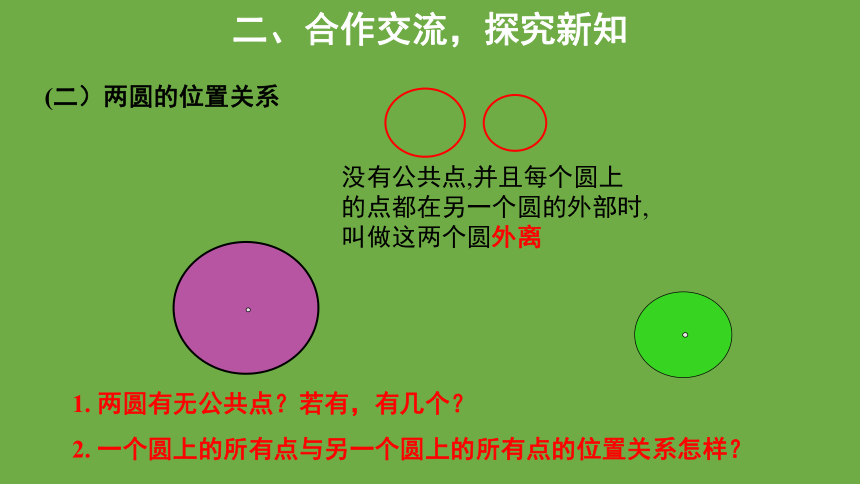
(二)两圆的位置关系
1. 两圆有无公共点?若有,有几个?
2. 一个圆上的所有点与另一个圆上的所有点的位置关系怎样?
没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
二、合作交流,探究新知
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆相切
二、合作交流,探究新知
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切
两圆有两个公共点,叫做这两个圆相交
二、合作交流,探究新知
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的内部时,叫做这两个圆内切
二、合作交流,探究新知
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切
两圆有两个公共点,叫做这两个圆相交
两圆没有公共点, 且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含(特例:同心)
二、合作交流,探究新知
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的内部时,叫做这两个圆内切
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切
两圆有两个公共点,叫做这两个圆相交
O1
O2
R
r
d
d: 两圆圆心的距离(圆心距)
二、合作交流,探究新知
外离
O1
O2
d
O1
O2
d
O1
O2
d
O1
O2
d
O1
O2
d
外切
相交
内含
内切
设大圆半径为 R,小圆半径为 r
二、合作交流,探究新知
外离
O1
O2
R
r
d > R + r
(三)圆心距与两圆半径的关系
设大圆半径为 R ,小圆半径为 r , = d
O2
O1
二、合作交流,探究新知
O1
O2
R
r
d=R+r
外切
设大圆半径为 R,小圆半径为 r , =d
O2
O1
二、合作交流,探究新知
O1
O2
R
r
R-r相交
设大圆半径为 R,小圆半径为 r, =d
O2
O1
二、合作交流,探究新知
O1
O2
R
r
d=R-r
内切
设大圆半径为 R,小圆半径为 r , =d
O2
O1
二、合作交流,探究新知
O1
O2
R
r
d内含
设大圆半径为 R ,小圆半径为 r , = d
O2
O1
二、合作交流,探究新知
位置 图形 交点个数 d与R、r的关系
外离
内含
外切
相离
相交
内切
相切
0
2
1
d>R+r
d<R-r
R-r <d<R+r
d=R+r
d=R-r
二、合作交流,探究新知
1. 已知两圆的半径分别是 3 和 7 ,圆心距为 d ,根据下列条件,确定 d 的取值范围。
⑴ 若两圆外切,则____________;
⑵ 若两圆内切,则____________;
⑶ 若两圆外离,则____________;
⑷ 若两圆内含,则____________;
⑸ 若两圆相交,则____________.
d=10
d>10
d<4
4<d<10
d=4
三、巩固新知
2. 判断下列说法是否正确
当两圆只有一个公共点时,两圆相切( )
当两圆无公共点时,两圆内含( )
两圆只有两个公共点时,两圆相交( )
两圆相切时有且只有一个公共点( )
只有外离、内含没有公共点( )
√
√
×
√
√
三、巩固新知
3. 已知⊙A ,⊙B相切,圆心距为10 cm,其中⊙A的半径为4 cm,求⊙B的半径.
解:设⊙B的半径为R
(1)如果两圆外切,则
(2)如果两圆内切,则
d=10=4+R
R=6
d=︱R-4︳=10
R=-6(舍去), R=14
答: ⊙B的半径为6 cm或14 cm
三、巩固新知
4. 如图,⊙O 的半径为 5 cm,点 P 是⊙ O外一点,OP = 8 cm,
求:(1)以 P 为圆心,作⊙ P 与⊙O 外切,小圆P的半径是多少?
(2)以P为圆心,作⊙P与⊙O内切,大圆P的半径是多少?
A
B
P
O
解:(1)设⊙O与⊙P外切于点A,则
(2)设⊙O与⊙P内切于点B,则
AP=OP-OA
∴ PA=8-5=3cm
PB=OP+OB=8+5=13cm
三、巩固新知
1. 复习了点与圆及直线与圆的位置关系
2. 学习两圆五种位置关系中两圆半径与圆心距的数量关系
图 形
性质及判定
公共点个数
外离
d>R+r
外切
d=R+r
外离
R-r内切
d=R-r
内含
d<R-r
没有
一个
两个
一个
没有
点在圆内、在圆上、在圆外
相离、相切、相交
四、归纳小结
再 见
第二十四章 圆
24.2 实验与探究
圆和圆的位置关系
1. 点与圆的位置关系
2. 直线与圆的位置关系
3. 两个圆的位置关系如何呢?这就是我们这节课要解决的问题
一、复习回顾
关系
点在圆内
点在圆上
点在圆外
数量特征
d
d>r
点和圆的三种位置关系
一、复习回顾
直线与圆的位置关系
公共点数目
公共点名称
直线名称
数量特征
直线和圆的三种位置关系
相交 相切 相离
2 1 0
交点 切点 无
割线 切线 无
d
一、复习回顾
(一)观察
请认真观察两圆的运动过程,注意两圆的位置关系
二、合作交流,探究新知
(二)两圆的位置关系
1. 两圆有无公共点?若有,有几个?
2. 一个圆上的所有点与另一个圆上的所有点的位置关系怎样?
没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
二、合作交流,探究新知
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆相切
二、合作交流,探究新知
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切
两圆有两个公共点,叫做这两个圆相交
二、合作交流,探究新知
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的内部时,叫做这两个圆内切
二、合作交流,探究新知
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切
两圆有两个公共点,叫做这两个圆相交
两圆没有公共点, 且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含(特例:同心)
二、合作交流,探究新知
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的内部时,叫做这两个圆内切
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切
两圆有两个公共点,叫做这两个圆相交
O1
O2
R
r
d
d: 两圆圆心的距离(圆心距)
二、合作交流,探究新知
外离
O1
O2
d
O1
O2
d
O1
O2
d
O1
O2
d
O1
O2
d
外切
相交
内含
内切
设大圆半径为 R,小圆半径为 r
二、合作交流,探究新知
外离
O1
O2
R
r
d > R + r
(三)圆心距与两圆半径的关系
设大圆半径为 R ,小圆半径为 r , = d
O2
O1
二、合作交流,探究新知
O1
O2
R
r
d=R+r
外切
设大圆半径为 R,小圆半径为 r , =d
O2
O1
二、合作交流,探究新知
O1
O2
R
r
R-r
设大圆半径为 R,小圆半径为 r, =d
O2
O1
二、合作交流,探究新知
O1
O2
R
r
d=R-r
内切
设大圆半径为 R,小圆半径为 r , =d
O2
O1
二、合作交流,探究新知
O1
O2
R
r
d
设大圆半径为 R ,小圆半径为 r , = d
O2
O1
二、合作交流,探究新知
位置 图形 交点个数 d与R、r的关系
外离
内含
外切
相离
相交
内切
相切
0
2
1
d>R+r
d<R-r
R-r <d<R+r
d=R+r
d=R-r
二、合作交流,探究新知
1. 已知两圆的半径分别是 3 和 7 ,圆心距为 d ,根据下列条件,确定 d 的取值范围。
⑴ 若两圆外切,则____________;
⑵ 若两圆内切,则____________;
⑶ 若两圆外离,则____________;
⑷ 若两圆内含,则____________;
⑸ 若两圆相交,则____________.
d=10
d>10
d<4
4<d<10
d=4
三、巩固新知
2. 判断下列说法是否正确
当两圆只有一个公共点时,两圆相切( )
当两圆无公共点时,两圆内含( )
两圆只有两个公共点时,两圆相交( )
两圆相切时有且只有一个公共点( )
只有外离、内含没有公共点( )
√
√
×
√
√
三、巩固新知
3. 已知⊙A ,⊙B相切,圆心距为10 cm,其中⊙A的半径为4 cm,求⊙B的半径.
解:设⊙B的半径为R
(1)如果两圆外切,则
(2)如果两圆内切,则
d=10=4+R
R=6
d=︱R-4︳=10
R=-6(舍去), R=14
答: ⊙B的半径为6 cm或14 cm
三、巩固新知
4. 如图,⊙O 的半径为 5 cm,点 P 是⊙ O外一点,OP = 8 cm,
求:(1)以 P 为圆心,作⊙ P 与⊙O 外切,小圆P的半径是多少?
(2)以P为圆心,作⊙P与⊙O内切,大圆P的半径是多少?
A
B
P
O
解:(1)设⊙O与⊙P外切于点A,则
(2)设⊙O与⊙P内切于点B,则
AP=OP-OA
∴ PA=8-5=3cm
PB=OP+OB=8+5=13cm
三、巩固新知
1. 复习了点与圆及直线与圆的位置关系
2. 学习两圆五种位置关系中两圆半径与圆心距的数量关系
图 形
性质及判定
公共点个数
外离
d>R+r
外切
d=R+r
外离
R-r
d=R-r
内含
d<R-r
没有
一个
两个
一个
没有
点在圆内、在圆上、在圆外
相离、相切、相交
四、归纳小结
再 见
同课章节目录
