完全平方公式:(甘肃)
图片预览



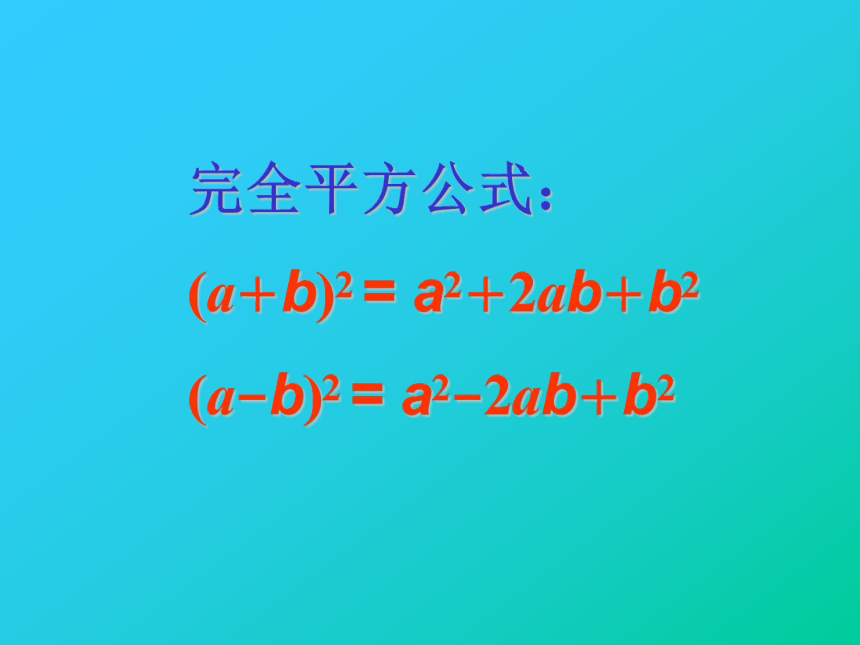

文档简介
课件13张PPT。标题第15章 整 式完全平方公式(1)标题一:动手实践,合作探究
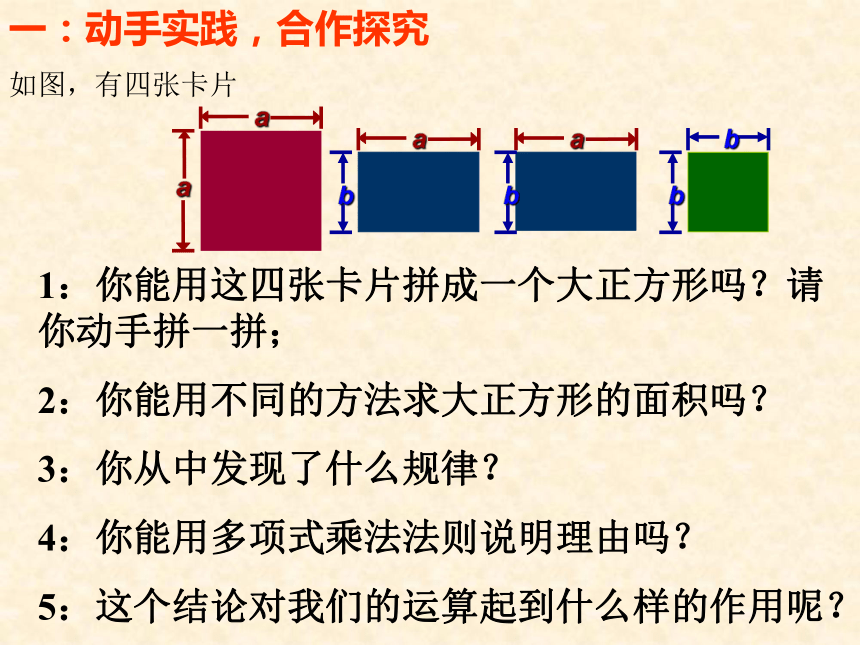
如图,有四张卡片
1:你能用这四张卡片拼成一个大正方形吗?请你动手拼一拼;
2:你能用不同的方法求大正方形的面积吗?
3:你从中发现了什么规律?
4:你能用多项式乘法法则说明理由吗?
5:这个结论对我们的运算起到什么样的作用呢?得出结论:(a+b)2 = a2+2ab+b2 其实,据有关资料表明,古代中国人在很多年以前就利用类似的图形认识了这个规律。三:自主探究
请你大胆猜想,科学验证
1:根据上面的结论,你能猜出(a-b)2 的结果吗?
2:你能用不同的方法验证你猜测的结果吗?
(a-b)2 = a2-2ab+b2完全平方公式:
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2
议一议
完全平方公式:(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2观察上面的完全平方公式,讨论下面的问题:
1:公式的左边有什么特点?
2:公式的右边有什么特点?符号又有何特点?
3:你能用自己的语言叙述这个公式吗?完全平方公式:即:两数和的平方,等于它们的平方和,加上它们的积的两倍。
两数差的平方,等于它们的平方和,减去它们的积的两倍。谐音记忆:
首平方,末平方,2倍的首末中间放,
符号与前一个样。学以致用:
例1:利用平方差公式计算
(2x-3)2
(4x+5y)2
(mn-a)2
(-2t-1)2做题后反思:
1:利用完全平方公式简便了我们的运算。2:利用完全平方公式时,我们应注意的一些问题有:
(1)中间项是积的2倍;
(2)各项的符号;
(3)该加括号的应加括号等。3:公式中的字母可以代表数字,也可以代表整式一试身手 (1) ( x ? 2y)2 ;
(2) (2xy+ x )2 ;1、利用完全平方公式计算:(n +1)2 ? n2;
(-x-y)2.生活在线:
老王去年承包了一块边长为a的正方形实验田,今年把实验田进行了扩建,建成了一个边长增加了2米的大正方形,问现在实验田的面积是多少?比原来增加了多少?本节课你的收获是什么?本节课你学到了什么?这节课你学到了什么知识?通过这节课的学习你有何感想与体会?思考:
如图,有四张卡片
1:你能用这四张卡片拼成一个大正方形吗?请你动手拼一拼;
2:你能用不同的方法求大正方形的面积吗?
3:你从中发现了什么规律?
4:你能用多项式乘法法则说明理由吗?
5:这个结论对我们的运算起到什么样的作用呢?得出结论:(a+b)2 = a2+2ab+b2 其实,据有关资料表明,古代中国人在很多年以前就利用类似的图形认识了这个规律。三:自主探究
请你大胆猜想,科学验证
1:根据上面的结论,你能猜出(a-b)2 的结果吗?
2:你能用不同的方法验证你猜测的结果吗?
(a-b)2 = a2-2ab+b2完全平方公式:
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2
议一议
完全平方公式:(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2观察上面的完全平方公式,讨论下面的问题:
1:公式的左边有什么特点?
2:公式的右边有什么特点?符号又有何特点?
3:你能用自己的语言叙述这个公式吗?完全平方公式:即:两数和的平方,等于它们的平方和,加上它们的积的两倍。
两数差的平方,等于它们的平方和,减去它们的积的两倍。谐音记忆:
首平方,末平方,2倍的首末中间放,
符号与前一个样。学以致用:
例1:利用平方差公式计算
(2x-3)2
(4x+5y)2
(mn-a)2
(-2t-1)2做题后反思:
1:利用完全平方公式简便了我们的运算。2:利用完全平方公式时,我们应注意的一些问题有:
(1)中间项是积的2倍;
(2)各项的符号;
(3)该加括号的应加括号等。3:公式中的字母可以代表数字,也可以代表整式一试身手 (1) ( x ? 2y)2 ;
(2) (2xy+ x )2 ;1、利用完全平方公式计算:(n +1)2 ? n2;
(-x-y)2.生活在线:
老王去年承包了一块边长为a的正方形实验田,今年把实验田进行了扩建,建成了一个边长增加了2米的大正方形,问现在实验田的面积是多少?比原来增加了多少?本节课你的收获是什么?本节课你学到了什么?这节课你学到了什么知识?通过这节课的学习你有何感想与体会?思考:
同课章节目录
