人教版高中数学必修第二册9.2.1总体取值规律的估计 第1课时 频率分布表和频率分布直方图 同步练习(含解析)
文档属性
| 名称 | 人教版高中数学必修第二册9.2.1总体取值规律的估计 第1课时 频率分布表和频率分布直方图 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 217.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览


文档简介
人教版高中数学必修第二册9.2.1总体取值规律的估计
第1课时 频率分布表和频率分布直方图 同步练习
一、选择题(本大题共7小题,每小题5分,共35分)
1.从一堆苹果中任取10个,称得它们的质量如下(单位:克):
125 120 122 105 130 114 116 95 120 134
则样本数据落在[114.5,124.5)内的频率为 ( )
A.0.2 B.0.3 C.0.4 D.0.5
2.已知样本数据:10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11,12,11,则它们的极差是 ( )
A.5 B.6 C.7 D.8
3.容量为100的样本,将其观测数据按从小到大的顺序分为8组,如下表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
则第三组的频数和频率分别是 ( )
A.14和0.14 B.0.14和14
C.和0.14 D.和
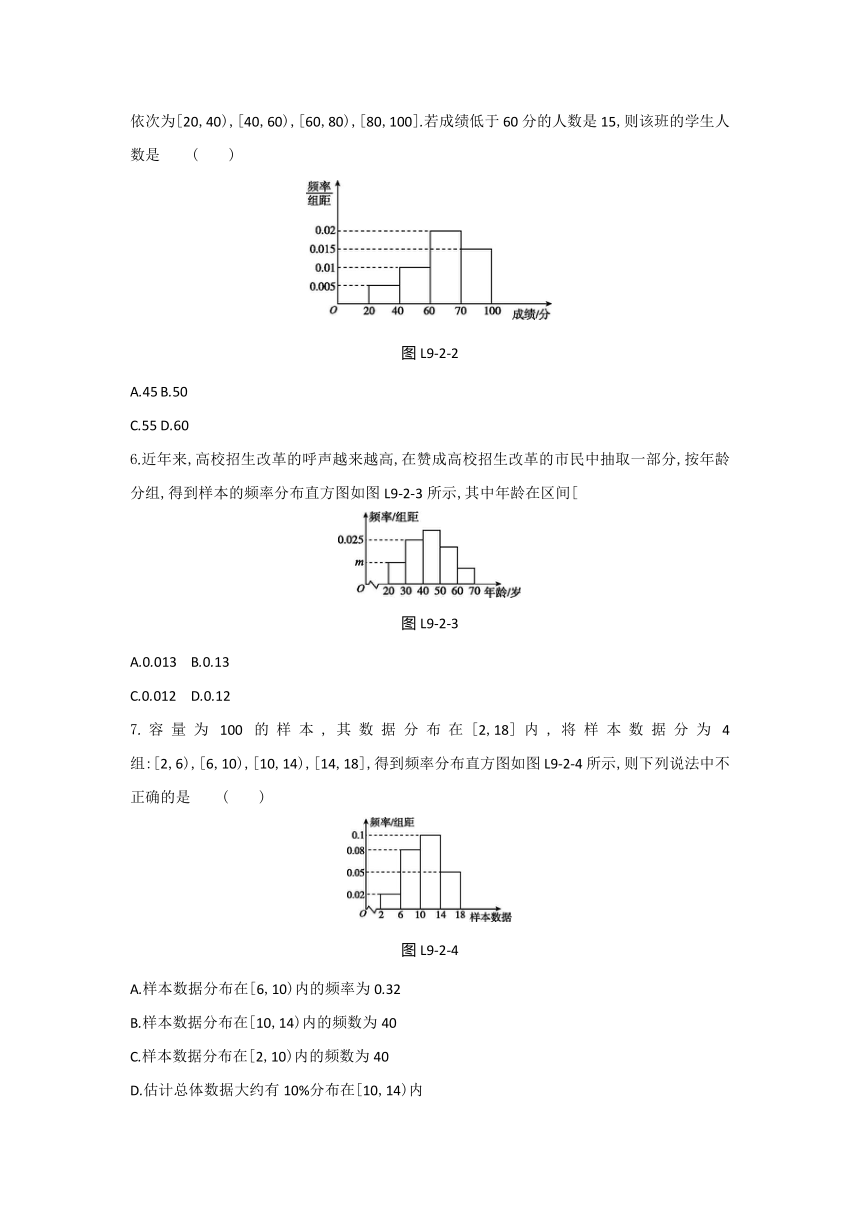
4.要调查某校1000名学生的学业水平测试的数学成绩,已知样本的频率分布直方图如图L9-2-1所示.若满分为100分,规定不低于60分为及格,则估计该校1000名学生的及格率是 ( )
图L9-2-1
A.20% B.25% C.60% D.80%
5.某班组织学生参加英语测试,得到其成绩的频率分布直方图如图L9-2-2所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若成绩低于60分的人数是15,则该班的学生人数是 ( )
图L9-2-2
A.45 B.50
C.55 D.60
6.近年来,高校招生改革的呼声越来越高,在赞成高校招生改革的市民中抽取一部分,按年龄分组,得到样本的频率分布直方图如图L9-2-3所示,其中年龄在区间[
图L9-2-3
A.0.013 B.0.13
C.0.012 D.0.12
7.容量为100的样本,其数据分布在[2,18]内,将样本数据分为4组:[2,6),[6,10),[10,14),[14,18],得到频率分布直方图如图L9-2-4所示,则下列说法中不正确的是 ( )
图L9-2-4
A.样本数据分布在[6,10)内的频率为0.32
B.样本数据分布在[10,14)内的频数为40
C.样本数据分布在[2,10)内的频数为40
D.估计总体数据大约有10%分布在[10,14)内
二、填空题(本大题共3小题,每小题5分,共15分)
8.一个容量为n的样本,将其观测数据分成若干组,已知甲组的频数和频率分别为36和,则n= ,频率为的乙组的频数x= .
9.某班的全体学生参加数学测试,成绩的频率分布直方图如图L9-2-5所示,若成绩低于60分的学生人数是15,则成绩不低于80分的学生人数是 .
图L9-2-5
10.在样本的频率分布直方图中共有n个小矩形,若中间一个小矩形的面积等于其余(n-1)个小矩形面积之和的,且样本量为3200,则中间一组的频数为 .
三、解答题(本大题共1小题,共10分)
11.(10分)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知如图L9-2-6所示的部分频率分布直方图,根据图中的信息,解答下列问题.
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)若60分及以上为及格,试估计这次考试的及格率.
图L9-2-6
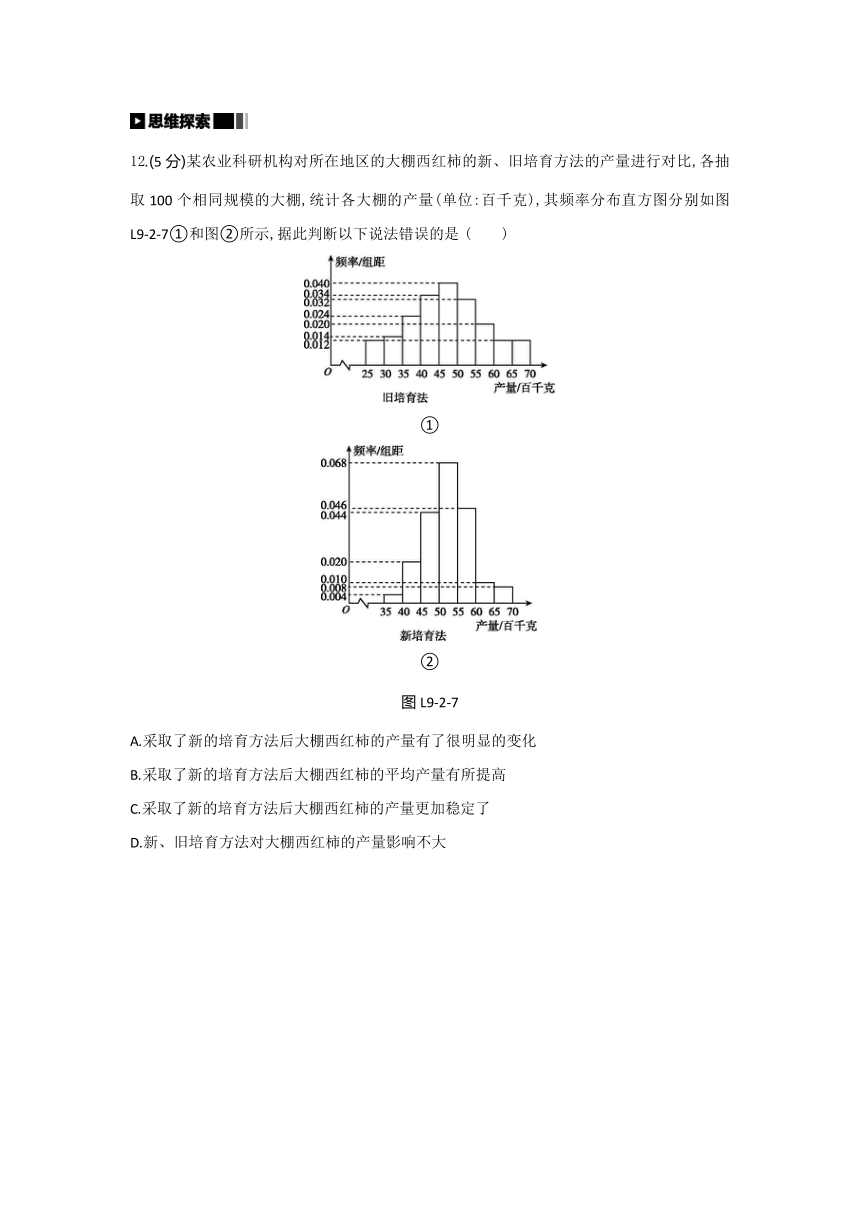
12.(5分)某农业科研机构对所在地区的大棚西红柿的新、旧培育方法的产量进行对比,各抽取100个相同规模的大棚,统计各大棚的产量(单位:百千克),其频率分布直方图分别如图L9-2-7①和图②所示,据此判断以下说法错误的是 ( )
①
②
图L9-2-7
A.采取了新的培育方法后大棚西红柿的产量有了很明显的变化
B.采取了新的培育方法后大棚西红柿的平均产量有所提高
C.采取了新的培育方法后大棚西红柿的产量更加稳定了
D.新、旧培育方法对大棚西红柿的产量影响不大
13.(15分)某市2019年4月1日至4月30日对空气质量指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
按[41,51),[51,61),…,[101,111]进行分组.
(1)作出频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,空气质量指数在0~50之间时,空气质量为优;空气质量指数在51~100之间时,空气质量为良;空气质量指数在101~150之间时,空气质量为轻度污染;空气质量指数在151~200之间时,空气质量为中度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
参考答案与解析
1.C [解析] 在125,120,122,105,130,114,116,95,120,134这10个数据中,落在[114.5,124.5)内的有120,122,116,120,共4个,∴样本数据落在[114.5,124.5)内的频率为=0.4.故选C.
2.C [解析] 由题知样本数据的最大值为13,最小值为6,故极差为13-6=7.
3.A [解析] 由题知x=100-(10+13+14+15+13+12+9)=100-86=14,故第三组的频数为14,频率为=0.14.
4.D [解析] 样本中及格的频率为(0.025+0.035+0.010+0.010)×10=0.8=80%,由样本估计总体,得及格率约为80%.故选D.
5.B [解析] 根据频率分布直方图可知成绩低于60分的为第一、二组数据,在频率分布直方图中,第一、二个矩形的高分别为0.005,0.01,每个矩形的底边长均为20,则该班学生成绩低于60分的频率为(0.005+0.01)×20=0.3.又因为成绩低于60分的人数是15,所以该班的学生人数是15÷0.3=50.故选B.
6.C [解析] 由题意得,年龄在区间[30,40)内的频率为0.025×10=0.25,则样本量为=10 000,因为年龄在区间[20,30)内的有1200人,所以m==0.012.
7.D [解析] 对于A,由图可得样本数据分布在[6,10)内的频率为0.08×4=0.32,所以A中说法正确.对于B,由图可得样本数据分布在[10,14)内的频数为100×(0.1×4)=40,所以B中说法正确.对于C,由图可得样本数据分布在[2,10)内的频数为100×(0.02+0.08)×4=40,所以C中说法正确.对于D,由图可估计总体数据分布在[10,14)内的有0.1×4=0.4=40%,故D中说法错误.故选D.
8.144 24 [解析] 由题意得=,所以n=36×4=144,同理=,解得x=24.
9.15 [解析] 根据题意,成绩低于60分的频率为(0.01+0.005)×20=0.3,又成绩低于60分的学生人数是15,所以该班总的学生人数为=50,根据频率分布直方图知成绩不低于80分的频率为0.015×20=0.3,故成绩不低于80分的学生人数是50×0.3=15.
10.400 [解析] 在样本的频率分布直方图中共有n个小矩形,中间一个小矩形的面积等于其余(n-1)个小矩形面积之和的,设中间一个小矩形的面积是x,则其余(n-1)个小矩形的面积之和为7x,∵x+7x=1,∴x=,∵样本量为3200,∴中间一组的频数是3200×=400.
11.解:(1)因为各组的频率之和等于1,所以第四小组的频率为1- (0.025+0.015×2+0.010+0.005)×10=0.3.
频率分布直方图中第四个小矩形的高是=0.030,
故可补全频率分布直方图如图所示.
(2)依题意知,60分及以上的成绩落在第三、四、五、六组,其频率之和为(0.015+0.030+0.025+0.005)×10=0.75,所以估计这次考试的及格率是75%.
12.D [解析] 在A中,采取了新的培育方法后大棚西红柿的产量有了很明显的变化,故A中说法正确;在B中,采取了新的培育方法后大棚西红柿的平均产量有所提高,故B中说法正确;在C中,采取了新的培育方法后大棚西红柿的产量更加稳定了,故C中说法正确;在D中,新、旧培育方法对大棚西红柿的产量影响较大,故D中说法错误.故选D.
13.解:(1)作出频率分布表如下表:
分组 频数 频率
[41,51) 2
[51,61) 1
[61,71) 4
[71,81) 6
[81,91) 10
[91,101) 5
[101,111] 2
(2)作出频率分布直方图如图所示.
(3)答对下述两条中的一条即可:
①该市一个月中空气质量指数有2天处于优的水平,占当月天数的;有26天处于良的水平,占当月天数的;处于优或良的天数为28,占当月天数的.说明该市空气质量基本良好.
②空气质量为轻度污染的有2天,占当月天数的;空气质量指数在81~100之间的天数为15,加上空气质量为轻度污染的天数2,占当月天数的,超过50%.说明该市空气质量有待进一步改善.
第1课时 频率分布表和频率分布直方图 同步练习
一、选择题(本大题共7小题,每小题5分,共35分)
1.从一堆苹果中任取10个,称得它们的质量如下(单位:克):
125 120 122 105 130 114 116 95 120 134
则样本数据落在[114.5,124.5)内的频率为 ( )
A.0.2 B.0.3 C.0.4 D.0.5
2.已知样本数据:10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11,12,11,则它们的极差是 ( )
A.5 B.6 C.7 D.8
3.容量为100的样本,将其观测数据按从小到大的顺序分为8组,如下表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
则第三组的频数和频率分别是 ( )
A.14和0.14 B.0.14和14
C.和0.14 D.和
4.要调查某校1000名学生的学业水平测试的数学成绩,已知样本的频率分布直方图如图L9-2-1所示.若满分为100分,规定不低于60分为及格,则估计该校1000名学生的及格率是 ( )
图L9-2-1
A.20% B.25% C.60% D.80%
5.某班组织学生参加英语测试,得到其成绩的频率分布直方图如图L9-2-2所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若成绩低于60分的人数是15,则该班的学生人数是 ( )
图L9-2-2
A.45 B.50
C.55 D.60
6.近年来,高校招生改革的呼声越来越高,在赞成高校招生改革的市民中抽取一部分,按年龄分组,得到样本的频率分布直方图如图L9-2-3所示,其中年龄在区间[
图L9-2-3
A.0.013 B.0.13
C.0.012 D.0.12
7.容量为100的样本,其数据分布在[2,18]内,将样本数据分为4组:[2,6),[6,10),[10,14),[14,18],得到频率分布直方图如图L9-2-4所示,则下列说法中不正确的是 ( )
图L9-2-4
A.样本数据分布在[6,10)内的频率为0.32
B.样本数据分布在[10,14)内的频数为40
C.样本数据分布在[2,10)内的频数为40
D.估计总体数据大约有10%分布在[10,14)内
二、填空题(本大题共3小题,每小题5分,共15分)
8.一个容量为n的样本,将其观测数据分成若干组,已知甲组的频数和频率分别为36和,则n= ,频率为的乙组的频数x= .
9.某班的全体学生参加数学测试,成绩的频率分布直方图如图L9-2-5所示,若成绩低于60分的学生人数是15,则成绩不低于80分的学生人数是 .
图L9-2-5
10.在样本的频率分布直方图中共有n个小矩形,若中间一个小矩形的面积等于其余(n-1)个小矩形面积之和的,且样本量为3200,则中间一组的频数为 .
三、解答题(本大题共1小题,共10分)
11.(10分)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知如图L9-2-6所示的部分频率分布直方图,根据图中的信息,解答下列问题.
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)若60分及以上为及格,试估计这次考试的及格率.
图L9-2-6
12.(5分)某农业科研机构对所在地区的大棚西红柿的新、旧培育方法的产量进行对比,各抽取100个相同规模的大棚,统计各大棚的产量(单位:百千克),其频率分布直方图分别如图L9-2-7①和图②所示,据此判断以下说法错误的是 ( )
①
②
图L9-2-7
A.采取了新的培育方法后大棚西红柿的产量有了很明显的变化
B.采取了新的培育方法后大棚西红柿的平均产量有所提高
C.采取了新的培育方法后大棚西红柿的产量更加稳定了
D.新、旧培育方法对大棚西红柿的产量影响不大
13.(15分)某市2019年4月1日至4月30日对空气质量指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
按[41,51),[51,61),…,[101,111]进行分组.
(1)作出频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,空气质量指数在0~50之间时,空气质量为优;空气质量指数在51~100之间时,空气质量为良;空气质量指数在101~150之间时,空气质量为轻度污染;空气质量指数在151~200之间时,空气质量为中度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
参考答案与解析
1.C [解析] 在125,120,122,105,130,114,116,95,120,134这10个数据中,落在[114.5,124.5)内的有120,122,116,120,共4个,∴样本数据落在[114.5,124.5)内的频率为=0.4.故选C.
2.C [解析] 由题知样本数据的最大值为13,最小值为6,故极差为13-6=7.
3.A [解析] 由题知x=100-(10+13+14+15+13+12+9)=100-86=14,故第三组的频数为14,频率为=0.14.
4.D [解析] 样本中及格的频率为(0.025+0.035+0.010+0.010)×10=0.8=80%,由样本估计总体,得及格率约为80%.故选D.
5.B [解析] 根据频率分布直方图可知成绩低于60分的为第一、二组数据,在频率分布直方图中,第一、二个矩形的高分别为0.005,0.01,每个矩形的底边长均为20,则该班学生成绩低于60分的频率为(0.005+0.01)×20=0.3.又因为成绩低于60分的人数是15,所以该班的学生人数是15÷0.3=50.故选B.
6.C [解析] 由题意得,年龄在区间[30,40)内的频率为0.025×10=0.25,则样本量为=10 000,因为年龄在区间[20,30)内的有1200人,所以m==0.012.
7.D [解析] 对于A,由图可得样本数据分布在[6,10)内的频率为0.08×4=0.32,所以A中说法正确.对于B,由图可得样本数据分布在[10,14)内的频数为100×(0.1×4)=40,所以B中说法正确.对于C,由图可得样本数据分布在[2,10)内的频数为100×(0.02+0.08)×4=40,所以C中说法正确.对于D,由图可估计总体数据分布在[10,14)内的有0.1×4=0.4=40%,故D中说法错误.故选D.
8.144 24 [解析] 由题意得=,所以n=36×4=144,同理=,解得x=24.
9.15 [解析] 根据题意,成绩低于60分的频率为(0.01+0.005)×20=0.3,又成绩低于60分的学生人数是15,所以该班总的学生人数为=50,根据频率分布直方图知成绩不低于80分的频率为0.015×20=0.3,故成绩不低于80分的学生人数是50×0.3=15.
10.400 [解析] 在样本的频率分布直方图中共有n个小矩形,中间一个小矩形的面积等于其余(n-1)个小矩形面积之和的,设中间一个小矩形的面积是x,则其余(n-1)个小矩形的面积之和为7x,∵x+7x=1,∴x=,∵样本量为3200,∴中间一组的频数是3200×=400.
11.解:(1)因为各组的频率之和等于1,所以第四小组的频率为1- (0.025+0.015×2+0.010+0.005)×10=0.3.
频率分布直方图中第四个小矩形的高是=0.030,
故可补全频率分布直方图如图所示.
(2)依题意知,60分及以上的成绩落在第三、四、五、六组,其频率之和为(0.015+0.030+0.025+0.005)×10=0.75,所以估计这次考试的及格率是75%.
12.D [解析] 在A中,采取了新的培育方法后大棚西红柿的产量有了很明显的变化,故A中说法正确;在B中,采取了新的培育方法后大棚西红柿的平均产量有所提高,故B中说法正确;在C中,采取了新的培育方法后大棚西红柿的产量更加稳定了,故C中说法正确;在D中,新、旧培育方法对大棚西红柿的产量影响较大,故D中说法错误.故选D.
13.解:(1)作出频率分布表如下表:
分组 频数 频率
[41,51) 2
[51,61) 1
[61,71) 4
[71,81) 6
[81,91) 10
[91,101) 5
[101,111] 2
(2)作出频率分布直方图如图所示.
(3)答对下述两条中的一条即可:
①该市一个月中空气质量指数有2天处于优的水平,占当月天数的;有26天处于良的水平,占当月天数的;处于优或良的天数为28,占当月天数的.说明该市空气质量基本良好.
②空气质量为轻度污染的有2天,占当月天数的;空气质量指数在81~100之间的天数为15,加上空气质量为轻度污染的天数2,占当月天数的,超过50%.说明该市空气质量有待进一步改善.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
