人教版高中数学必修第二册9.2.2总体百分位数的估计 同步练习(含解析)
文档属性
| 名称 | 人教版高中数学必修第二册9.2.2总体百分位数的估计 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 248.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览



文档简介
人教版高中数学必修第二册9.2.2总体百分位数的估计 同步练习
一、选择题(本大题共8小题,每小题5分,共40分)
1.1至10排列的10个整数中,第60百分位数是 ( )
A.5 B.5.5 C.6 D.6.5
2.给出一组数据:8,8,7,6,5,4,其40%分位数是 ( )
A.8 B.7 C.6 D.5
3.已知按从小到大的顺序排列的一组数据:3,6,a,b,12,若其60%分位数为8,则下列情况可能的是 ( )
A.a=7,b=9 B.a=7,b=10
C.a=8,b=9 D.a=8,b=10
4.2至20排列的10个偶数中,下四分位数是 ( )
A.6 B.6.5 C.7 D.7.5
5.如图L9-2-22是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,由图可知这10天的最低气温的第80百分位数是 ( )
图L9-2-22
A.-2 ℃ B.0 ℃ C.1 ℃ D.2 ℃
6.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.现随机抽取10位北京市民,他们的幸福感指数为3,4,5,5,6,7,7,8,9,10.则这组数据的75%分位数是 ( )
A.7 B.7.5 C.8 D.8.5
7.某厂10名工人在一小时内生产零件的个数分别是15,17,14,10,15,17,17,16,14,12,设该组数据的平均数为a,第50百分位数为b,则有 ( )
A.a=13.7, b=15.5 B.a=14,b=15
C.a=12, b=15.5 D.a=14.7, b=15
8.某棉纺厂为了了解一批棉花的质量,从中随机抽测了100根棉花的纤维长度(棉花的纤维长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图L9-2-23所示.估计棉花的纤维长度的样本数据的80%分位数是 ( )
图L9-2-23
A.28 mm B.28.5 mm
C.29 mm D.29.5 mm
二、填空题(本大题共4小题,每小题5分,共20分)
9.数据7.0,8.4,8.4,8.4,8.6,8.7,9.0,9.1的第30百分位数是 .
10.某组数据的中位数是2019,那么它的第50百分位数是 .
11.一组样本数据的频率分布直方图如图L9-2-24所示,试估计此样本数据的第50百分位数为 .
图L9-2-24
12.已知30个数据的第60百分位数是8.2,这30个数据从小到大排列后第18个数据是7.8,则第19个数据是 .
三、解答题(本大题共2小题,共20分)
13.(10分)某网络营销部门随机抽查了某市200名网友在2019年11月11日的网购金额,所得数据如下表:
网购金额(单位:千元) 人数 频率
(0,1] 16 0.08
(1,2] 24 0.12
(2,3] x p
(3,4] y q
(4,5] 16 0.08
(5,6] 14 0.07
合计 200 1.00
已知网购金额不超过3千元与超过3千元的人数比恰为3∶2.
(1)试确定x,y,p,q的值,并补全频率分布直方图(如图L9-2-25).
(2)估计网购金额的25%分位数(结果保留3位有效数字).
图L9-2-25
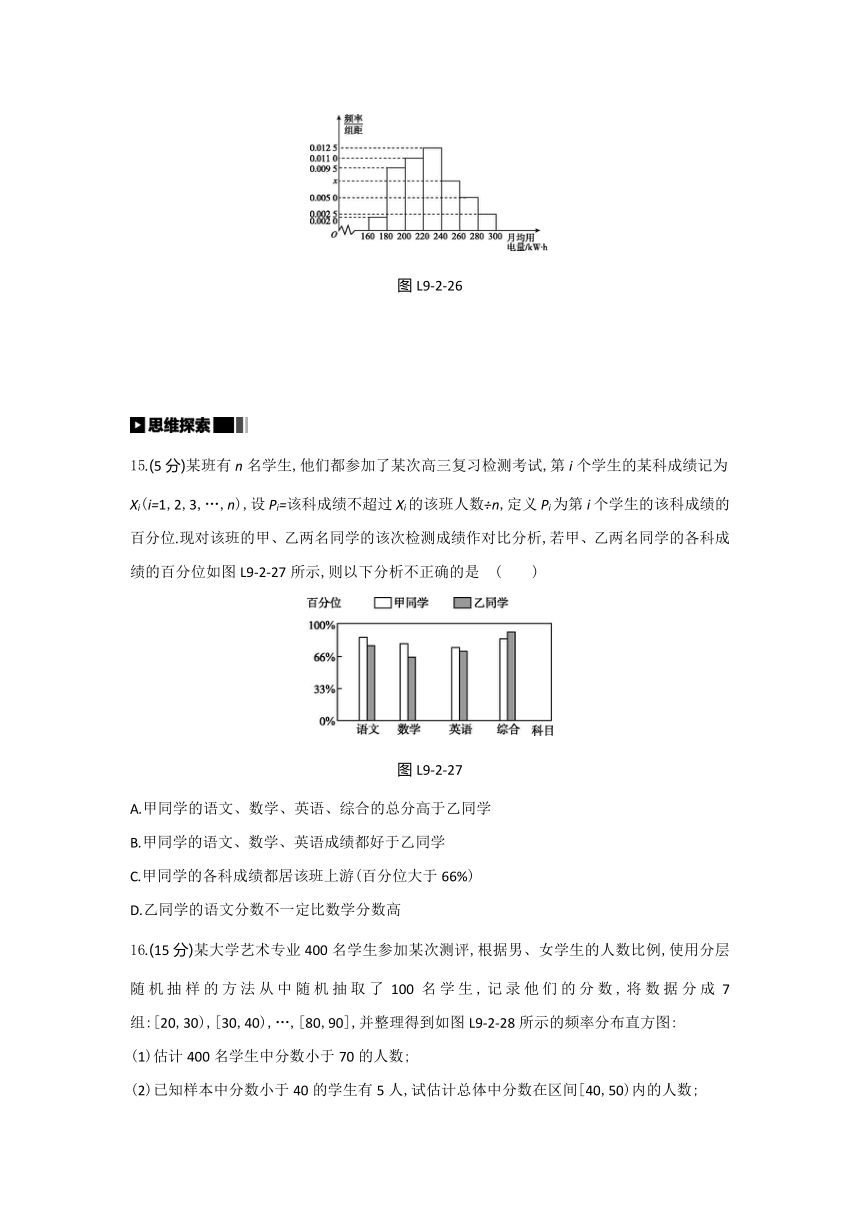
14.(10分)为了了解居民的用电情况,某市供电局抽查了该市若干户居民的月均用电量(单位:kW·h),并将样本数据分组为[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300] ,其频率分布直方图如图L9-2-26所示.
(1)若样本中月均用电量在[240,260)内的居民有30户,求样本量;
(2)求样本中月均用电量的中位数;
(3)在月均用电量为[220,240),[240,260),[260,280),[280,300]的四组居民中,用比例分配的分层随机抽样的方法抽取22户居民,则月均用电量在[260,280)内的居民应抽取多少户
图L9-2-26
15.(5分)某班有n名学生,他们都参加了某次高三复习检测考试,第i个学生的某科成绩记为Xi(i=1,2,3,…,n),设Pi=该科成绩不超过Xi的该班人数÷n,定义Pi为第i个学生的该科成绩的百分位.现对该班的甲、乙两名同学的该次检测成绩作对比分析,若甲、乙两名同学的各科成绩的百分位如图L9-2-27所示,则以下分析不正确的是 ( )
图L9-2-27
A.甲同学的语文、数学、英语、综合的总分高于乙同学
B.甲同学的语文、数学、英语成绩都好于乙同学
C.甲同学的各科成绩都居该班上游(百分位大于66%)
D.乙同学的语文分数不一定比数学分数高
16.(15分)某大学艺术专业400名学生参加某次测评,根据男、女学生的人数比例,使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如图L9-2-28所示的频率分布直方图:
(1)估计400名学生中分数小于70的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)根据该大学规定,把15%的学生划定为不及格,利用(2)中的数据,确定本次测试的及格分数线.
图L9-2-28
参考答案与解析
1.D [解析] 由i=n×p%=10×60%=6,可知第60百分位数为=6.5.故选D.
2.C [解析] 将这6个数从小到大重新排列:4,5,6,7,8,8.i=6×40%=2.4,所以其40%分位数是第3个数,即6.
3.A [解析] i=5×60%=3,所以60%分位数为第3项和第4项的数据的平均数,即=8,所以a+b=16.故选A.
4.A [解析] 由i=n×p%=10×25%=2.5,可知下四分位数为第3项数据,即6.故选A.
5.D [解析] 由折线图可知,这10天的最低气温(℃)按照从小到大排列为:-3,-2,-1,-1,0,0,1,2,2,2,因为共有10个数据,所以10×80%=8,是整数,则这10天的最低气温的第80百分位数是=2(℃).
6.C [解析] 由题意,这10个人的幸福感指数已经从小到大排列,因为75%×10=7.5,所以这组数据的75%分位数是第8个数据,即8.故选C.
7.D [解析] 把该组数据按从小到大的顺序排列为10,12,14,14,15,15,16,17,17,17,其平均数a=×(10+12+14+14+15+15+16+17+17+17)=14.7,第50百分位数为b==15.
8.C [解析] 棉花的纤维长度在25 mm以下的频率为(0.01+0.01+0.04+0.06)×5=0.6=60%,在30 mm以下的频率为60%+25%=85%,因此,80%分位数一定位于[25,30)内,由25+5×=29,可以估计棉花的纤维长度的样本数据的80%分位数是29 mm.
9.8.4 [解析] 因为8×30%=2.4,故第30百分位数是第三项数据8.4.
10.2019 [解析] 某组数据的中位数是2019,第50百分位数就相当于中位数,故它的第50百分位数是2019.
11. [解析] 样本数据小于10的比例为(0.02+0.08)×4=0.40,样本数据小于14的比例为0.40+0.09×4=0.76,所以此样本数据的第50百分位数在[10,14)内,估计此样本数据的第50百分位数为10+×4=.
12.8.6 [解析] 30×60%=18,设第19个数据为x,则=8.2,解得x=8.6,即第19个数据是8.6.
13.解:(1)根据题意有解得所以p=0.4,q=0.25.
补全频率分布直方图如图所示.
(2)由(1)可知,网购金额不高于2千元的频率为0.08+0.12=0.2,网购金额不高于3千元的频率为0.2+0.4=0.6,所以网购金额的25%分位数在(2,3]内,
故网购金额的25%分位数约为2+×1=2.125(千元).
14.解:(1)由题知(0.002 0+0.009 5+0.011 0+0.012 5+x+0.005 0+0.002 5)×20=1,
解得x=0.007 5.∴ 月均用电量在[240,260)内的频率为0.007 5×20=0.15.
设样本量为N,则0.15N=30,解得N=200.
(2)∵(0.002 0+0.009 5+0.011 0)×20=0.45<0.5,0.012 5×20=0.25,
∴ 月均用电量的中位数在[220,240)内.
设中位数为a kW·h,则0.45+0.012 5×(a-220)=0.5,
解得a=224,即中位数为224 kW·h.
(3)月均用电量为[220,240),[240,260),[260,280),[280,300]的频率分别为0.25,0.15,0.1,0.05.∴ 应从月均用电量在[260,280)内的居民中抽取22×=4(户).
15.A [解析] 由甲、乙两名同学的各科成绩的百分位图可知,在A中,甲同学的语文、数学、英语三科得分高于乙同学,综合得分低于乙同学,∴甲同学的语文、数学、英语、综合的总分不一定高于乙同学,故A错误;在B中,甲同学的语文、数学、英语成绩都好于乙同学,故B正确;在C中,甲同学的各科成绩百分位均超过66%,∴甲同学的各科成绩都居该班的上游,故C正确;在D中,乙同学的语文分数不一定比数学分数高,故D正确.故选A.
16.解:(1)根据频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.
所以400名学生中分数小于70的人数为400×0.4=160.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,分数在区间[40,50)内的人数为100-100×0.9-5=5.
所以总体中分数在区间[40,50)内的人数约为400×=20.
(3)设样本中分数的第15百分位数为x,由(2)可知,分数小于50的频率为=0.1,分数小于60的频率为0.1+0.1=0.2,所以x∈[50,60),则0.1+(x-50)×0.01=0.15,解得x=55,所以本次考试的及格分数线为55.
一、选择题(本大题共8小题,每小题5分,共40分)
1.1至10排列的10个整数中,第60百分位数是 ( )
A.5 B.5.5 C.6 D.6.5
2.给出一组数据:8,8,7,6,5,4,其40%分位数是 ( )
A.8 B.7 C.6 D.5
3.已知按从小到大的顺序排列的一组数据:3,6,a,b,12,若其60%分位数为8,则下列情况可能的是 ( )
A.a=7,b=9 B.a=7,b=10
C.a=8,b=9 D.a=8,b=10
4.2至20排列的10个偶数中,下四分位数是 ( )
A.6 B.6.5 C.7 D.7.5
5.如图L9-2-22是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,由图可知这10天的最低气温的第80百分位数是 ( )
图L9-2-22
A.-2 ℃ B.0 ℃ C.1 ℃ D.2 ℃
6.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.现随机抽取10位北京市民,他们的幸福感指数为3,4,5,5,6,7,7,8,9,10.则这组数据的75%分位数是 ( )
A.7 B.7.5 C.8 D.8.5
7.某厂10名工人在一小时内生产零件的个数分别是15,17,14,10,15,17,17,16,14,12,设该组数据的平均数为a,第50百分位数为b,则有 ( )
A.a=13.7, b=15.5 B.a=14,b=15
C.a=12, b=15.5 D.a=14.7, b=15
8.某棉纺厂为了了解一批棉花的质量,从中随机抽测了100根棉花的纤维长度(棉花的纤维长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图L9-2-23所示.估计棉花的纤维长度的样本数据的80%分位数是 ( )
图L9-2-23
A.28 mm B.28.5 mm
C.29 mm D.29.5 mm
二、填空题(本大题共4小题,每小题5分,共20分)
9.数据7.0,8.4,8.4,8.4,8.6,8.7,9.0,9.1的第30百分位数是 .
10.某组数据的中位数是2019,那么它的第50百分位数是 .
11.一组样本数据的频率分布直方图如图L9-2-24所示,试估计此样本数据的第50百分位数为 .
图L9-2-24
12.已知30个数据的第60百分位数是8.2,这30个数据从小到大排列后第18个数据是7.8,则第19个数据是 .
三、解答题(本大题共2小题,共20分)
13.(10分)某网络营销部门随机抽查了某市200名网友在2019年11月11日的网购金额,所得数据如下表:
网购金额(单位:千元) 人数 频率
(0,1] 16 0.08
(1,2] 24 0.12
(2,3] x p
(3,4] y q
(4,5] 16 0.08
(5,6] 14 0.07
合计 200 1.00
已知网购金额不超过3千元与超过3千元的人数比恰为3∶2.
(1)试确定x,y,p,q的值,并补全频率分布直方图(如图L9-2-25).
(2)估计网购金额的25%分位数(结果保留3位有效数字).
图L9-2-25
14.(10分)为了了解居民的用电情况,某市供电局抽查了该市若干户居民的月均用电量(单位:kW·h),并将样本数据分组为[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300] ,其频率分布直方图如图L9-2-26所示.
(1)若样本中月均用电量在[240,260)内的居民有30户,求样本量;
(2)求样本中月均用电量的中位数;
(3)在月均用电量为[220,240),[240,260),[260,280),[280,300]的四组居民中,用比例分配的分层随机抽样的方法抽取22户居民,则月均用电量在[260,280)内的居民应抽取多少户
图L9-2-26
15.(5分)某班有n名学生,他们都参加了某次高三复习检测考试,第i个学生的某科成绩记为Xi(i=1,2,3,…,n),设Pi=该科成绩不超过Xi的该班人数÷n,定义Pi为第i个学生的该科成绩的百分位.现对该班的甲、乙两名同学的该次检测成绩作对比分析,若甲、乙两名同学的各科成绩的百分位如图L9-2-27所示,则以下分析不正确的是 ( )
图L9-2-27
A.甲同学的语文、数学、英语、综合的总分高于乙同学
B.甲同学的语文、数学、英语成绩都好于乙同学
C.甲同学的各科成绩都居该班上游(百分位大于66%)
D.乙同学的语文分数不一定比数学分数高
16.(15分)某大学艺术专业400名学生参加某次测评,根据男、女学生的人数比例,使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如图L9-2-28所示的频率分布直方图:
(1)估计400名学生中分数小于70的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)根据该大学规定,把15%的学生划定为不及格,利用(2)中的数据,确定本次测试的及格分数线.
图L9-2-28
参考答案与解析
1.D [解析] 由i=n×p%=10×60%=6,可知第60百分位数为=6.5.故选D.
2.C [解析] 将这6个数从小到大重新排列:4,5,6,7,8,8.i=6×40%=2.4,所以其40%分位数是第3个数,即6.
3.A [解析] i=5×60%=3,所以60%分位数为第3项和第4项的数据的平均数,即=8,所以a+b=16.故选A.
4.A [解析] 由i=n×p%=10×25%=2.5,可知下四分位数为第3项数据,即6.故选A.
5.D [解析] 由折线图可知,这10天的最低气温(℃)按照从小到大排列为:-3,-2,-1,-1,0,0,1,2,2,2,因为共有10个数据,所以10×80%=8,是整数,则这10天的最低气温的第80百分位数是=2(℃).
6.C [解析] 由题意,这10个人的幸福感指数已经从小到大排列,因为75%×10=7.5,所以这组数据的75%分位数是第8个数据,即8.故选C.
7.D [解析] 把该组数据按从小到大的顺序排列为10,12,14,14,15,15,16,17,17,17,其平均数a=×(10+12+14+14+15+15+16+17+17+17)=14.7,第50百分位数为b==15.
8.C [解析] 棉花的纤维长度在25 mm以下的频率为(0.01+0.01+0.04+0.06)×5=0.6=60%,在30 mm以下的频率为60%+25%=85%,因此,80%分位数一定位于[25,30)内,由25+5×=29,可以估计棉花的纤维长度的样本数据的80%分位数是29 mm.
9.8.4 [解析] 因为8×30%=2.4,故第30百分位数是第三项数据8.4.
10.2019 [解析] 某组数据的中位数是2019,第50百分位数就相当于中位数,故它的第50百分位数是2019.
11. [解析] 样本数据小于10的比例为(0.02+0.08)×4=0.40,样本数据小于14的比例为0.40+0.09×4=0.76,所以此样本数据的第50百分位数在[10,14)内,估计此样本数据的第50百分位数为10+×4=.
12.8.6 [解析] 30×60%=18,设第19个数据为x,则=8.2,解得x=8.6,即第19个数据是8.6.
13.解:(1)根据题意有解得所以p=0.4,q=0.25.
补全频率分布直方图如图所示.
(2)由(1)可知,网购金额不高于2千元的频率为0.08+0.12=0.2,网购金额不高于3千元的频率为0.2+0.4=0.6,所以网购金额的25%分位数在(2,3]内,
故网购金额的25%分位数约为2+×1=2.125(千元).
14.解:(1)由题知(0.002 0+0.009 5+0.011 0+0.012 5+x+0.005 0+0.002 5)×20=1,
解得x=0.007 5.∴ 月均用电量在[240,260)内的频率为0.007 5×20=0.15.
设样本量为N,则0.15N=30,解得N=200.
(2)∵(0.002 0+0.009 5+0.011 0)×20=0.45<0.5,0.012 5×20=0.25,
∴ 月均用电量的中位数在[220,240)内.
设中位数为a kW·h,则0.45+0.012 5×(a-220)=0.5,
解得a=224,即中位数为224 kW·h.
(3)月均用电量为[220,240),[240,260),[260,280),[280,300]的频率分别为0.25,0.15,0.1,0.05.∴ 应从月均用电量在[260,280)内的居民中抽取22×=4(户).
15.A [解析] 由甲、乙两名同学的各科成绩的百分位图可知,在A中,甲同学的语文、数学、英语三科得分高于乙同学,综合得分低于乙同学,∴甲同学的语文、数学、英语、综合的总分不一定高于乙同学,故A错误;在B中,甲同学的语文、数学、英语成绩都好于乙同学,故B正确;在C中,甲同学的各科成绩百分位均超过66%,∴甲同学的各科成绩都居该班的上游,故C正确;在D中,乙同学的语文分数不一定比数学分数高,故D正确.故选A.
16.解:(1)根据频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.
所以400名学生中分数小于70的人数为400×0.4=160.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,分数在区间[40,50)内的人数为100-100×0.9-5=5.
所以总体中分数在区间[40,50)内的人数约为400×=20.
(3)设样本中分数的第15百分位数为x,由(2)可知,分数小于50的频率为=0.1,分数小于60的频率为0.1+0.1=0.2,所以x∈[50,60),则0.1+(x-50)×0.01=0.15,解得x=55,所以本次考试的及格分数线为55.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
