沪科版九年级上册第一次月考数学试题(含答案)
文档属性
| 名称 | 沪科版九年级上册第一次月考数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 09:46:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
沪科版九年级上册数学第一次月考试题
一、单选题。本大题共10小题,每小题3分,共30分。
1.下列函数中是二次函数的为( )
A.y=3x-1 B.y=3x2-1
C.y=(x+1)2-x2 D.y=x3+2x-3
2.如果反比例函数的图象经过点,那么这个函数的解析式为( )
A.y= B.y= C.y= D.y=-
3.2011年5月22日—29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛.在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-x2+bx+c的一部分(如图),其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物线的解析式是( )
A. B.
C. D.
4.正比例函数的图象与反比例函数的图象的交点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第一、三象限
5.二次函数和反比例函数在同一直角坐标系中的大致图象是( )
A. B. C. D.
6.购买斤水果需元,购买一斤水果的单价与的关系式是( )
A. B.(为自然数)
C.(为整数) D.(为正整数)
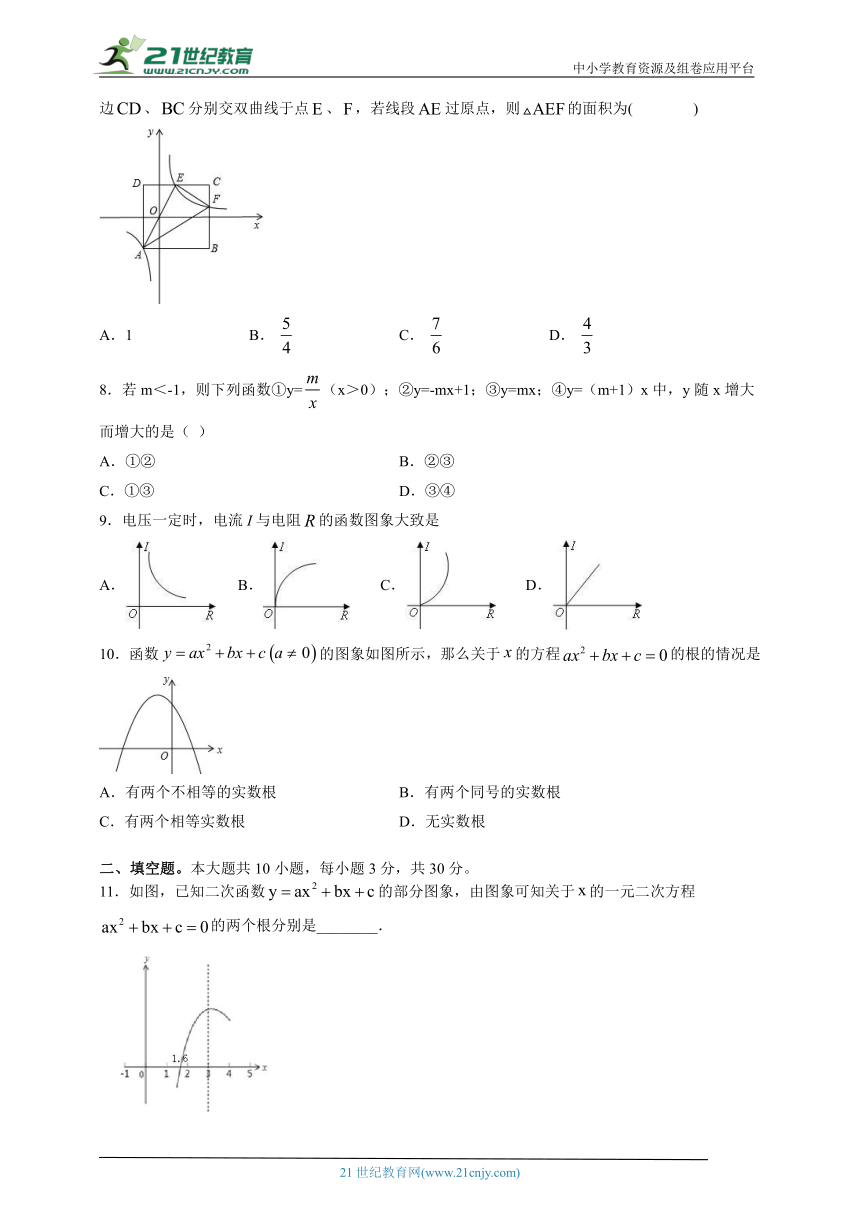
7.如图,正方形边长为,轴,轴,顶点恰好落在双曲线上,边、分别交双曲线于点、,若线段过原点,则的面积为( )
A.1 B. C. D.
8.若m<-1,则下列函数①y=(x>0);②y=-mx+1;③y=mx;④y=(m+1)x中,y随x增大而增大的是( )
A.①② B.②③
C.①③ D.③④
9.电压一定时,电流I与电阻的函数图象大致是
A. B. C. D.
10.函数的图象如图所示,那么关于的方程的根的情况是
A.有两个不相等的实数根 B.有两个同号的实数根
C.有两个相等实数根 D.无实数根
二、填空题。本大题共10小题,每小题3分,共30分。
11.如图,已知二次函数的部分图象,由图象可知关于的一元二次方程的两个根分别是________.
12.已知二次函数,当时,.则这个二次函数的表达式是________.
13.如图点、以原点为位似中心,把作位似变换,得到且使与周长的比为,那么点的对应点的坐标可以是________.(写出一个符合要求的即可)
14.若,则________.
15.某旅行社有张床位,每床每日收费元,客床可全部租出,若每床每日收费提高元,则租出床位减少张.若每床每日收费再提高元,则租出床位再减少张.以每提高元的这种方法变化下去,为了投资少而获利大,每床每日应提高________元.
16.已知三个数、、,请你添加一个数,使他们构成一个比例式,则这个数可能是________.(写出所有可能的数)
17.科学研究表明,当人的下肢与身高比为时,看起来最美,某成年女士身高为,下肢长为,该女士穿的高跟鞋鞋跟的最佳高度约为________(精确到).
18.下列函数中,是的反比例函数的有________.(填序号)
①;②;③;④;⑤;⑥.
19.在中,交于,交于,,,,那么________.
20.某学校去年对实验器材投资为2万元,预计今明两年的投资总额为y万元,年平均增长率为 x.则y与x的函数解析式______________.
三、解答题。本大题共6小题,共60分。
21.(8分)如图,在中,,将绕点旋转,点落在点处,点落在点处,,交于点,连接,,找出其中相似三角形.
22.(12分)已知关于的二次函数与,这两个二次函数的图象中的一条与轴交于,两个不同的点.
试判断哪个二次函数的图象经过,两点;
若点坐标为,试求点坐标;
在的条件下,对于经过,两点的二次函数,当取何值时,的值随值的增大而减小.
23.(10分)已知:在平面直角坐标系中,过点向轴作垂线,垂足为,连接,点在线段上,且,反比例函数的图象经过点,与边交于点.
求反比例函数的解析式;
求的面积.
24.(10分)如图,中,,,.长为的线段在的边上沿方向以的速度向点运动(运动前点与点重合).过,分别作的垂线交直角边于,两点,线段运动的时间为.
若的面积为,写出与的函数关系式(写出自变量的取值范围);
线段运动过程中,四边形有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;
为何值时,以,,为顶点的三角形与相似?
25.(10分)已知:如图,在梯形中,,点在边上,与相交于点,,,,.
求证:;
求线段的长.
26.(10分)善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间(单位:分钟)与学习收益量的关系如图1所示,用于回顾反思的时间(单位:分钟)与学习收益的关系如图2所示(其中是抛物线的一部分,为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量与用于解题的时间之间的函数关系式;
(2)求小迪回顾反思的学习收益量与用于回顾反思的时间的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
参考答案
1.B
2.C
3.A
4.D
5.B
6.A
7.D
8.A
9.A
10.A
11.,
12.
13.或
14.
15.
16.
17.
18.①②③④
19.
20.
21.,,,,,;理由略.
22.图象经过、两点的二次函数为; 点的坐标是或; 略.
23.反比例函数的解析式为; .
24.或;时,四边形为矩形;(3)当或时,以,,为顶点的三角形与相似.
25.(1)证明略;(2)CF=5.
26.解:(1)由图1,设.当时,,
解得,.
(2)由图2,当时,设.
当时,,
.
.
,即.
当时,.
因此
(3)设小迪用于回顾反思的时间为分钟,
学习收益总量为,则她用于解题的时间为分钟.
当时,.
当时,.
当时,.
随的增大而减小,因此当时,.
综上,当时,,此时.
答:小迪用于回顾反思的时间为3分钟,用于解题的时间为17分钟时,学习收益总量最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版九年级上册数学第一次月考试题
一、单选题。本大题共10小题,每小题3分,共30分。
1.下列函数中是二次函数的为( )
A.y=3x-1 B.y=3x2-1
C.y=(x+1)2-x2 D.y=x3+2x-3
2.如果反比例函数的图象经过点,那么这个函数的解析式为( )
A.y= B.y= C.y= D.y=-
3.2011年5月22日—29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛.在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-x2+bx+c的一部分(如图),其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物线的解析式是( )
A. B.
C. D.
4.正比例函数的图象与反比例函数的图象的交点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第一、三象限
5.二次函数和反比例函数在同一直角坐标系中的大致图象是( )
A. B. C. D.
6.购买斤水果需元,购买一斤水果的单价与的关系式是( )
A. B.(为自然数)
C.(为整数) D.(为正整数)
7.如图,正方形边长为,轴,轴,顶点恰好落在双曲线上,边、分别交双曲线于点、,若线段过原点,则的面积为( )
A.1 B. C. D.
8.若m<-1,则下列函数①y=(x>0);②y=-mx+1;③y=mx;④y=(m+1)x中,y随x增大而增大的是( )
A.①② B.②③
C.①③ D.③④
9.电压一定时,电流I与电阻的函数图象大致是
A. B. C. D.
10.函数的图象如图所示,那么关于的方程的根的情况是
A.有两个不相等的实数根 B.有两个同号的实数根
C.有两个相等实数根 D.无实数根
二、填空题。本大题共10小题,每小题3分,共30分。
11.如图,已知二次函数的部分图象,由图象可知关于的一元二次方程的两个根分别是________.
12.已知二次函数,当时,.则这个二次函数的表达式是________.
13.如图点、以原点为位似中心,把作位似变换,得到且使与周长的比为,那么点的对应点的坐标可以是________.(写出一个符合要求的即可)
14.若,则________.
15.某旅行社有张床位,每床每日收费元,客床可全部租出,若每床每日收费提高元,则租出床位减少张.若每床每日收费再提高元,则租出床位再减少张.以每提高元的这种方法变化下去,为了投资少而获利大,每床每日应提高________元.
16.已知三个数、、,请你添加一个数,使他们构成一个比例式,则这个数可能是________.(写出所有可能的数)
17.科学研究表明,当人的下肢与身高比为时,看起来最美,某成年女士身高为,下肢长为,该女士穿的高跟鞋鞋跟的最佳高度约为________(精确到).
18.下列函数中,是的反比例函数的有________.(填序号)
①;②;③;④;⑤;⑥.
19.在中,交于,交于,,,,那么________.
20.某学校去年对实验器材投资为2万元,预计今明两年的投资总额为y万元,年平均增长率为 x.则y与x的函数解析式______________.
三、解答题。本大题共6小题,共60分。
21.(8分)如图,在中,,将绕点旋转,点落在点处,点落在点处,,交于点,连接,,找出其中相似三角形.
22.(12分)已知关于的二次函数与,这两个二次函数的图象中的一条与轴交于,两个不同的点.
试判断哪个二次函数的图象经过,两点;
若点坐标为,试求点坐标;
在的条件下,对于经过,两点的二次函数,当取何值时,的值随值的增大而减小.
23.(10分)已知:在平面直角坐标系中,过点向轴作垂线,垂足为,连接,点在线段上,且,反比例函数的图象经过点,与边交于点.
求反比例函数的解析式;
求的面积.
24.(10分)如图,中,,,.长为的线段在的边上沿方向以的速度向点运动(运动前点与点重合).过,分别作的垂线交直角边于,两点,线段运动的时间为.
若的面积为,写出与的函数关系式(写出自变量的取值范围);
线段运动过程中,四边形有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;
为何值时,以,,为顶点的三角形与相似?
25.(10分)已知:如图,在梯形中,,点在边上,与相交于点,,,,.
求证:;
求线段的长.
26.(10分)善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间(单位:分钟)与学习收益量的关系如图1所示,用于回顾反思的时间(单位:分钟)与学习收益的关系如图2所示(其中是抛物线的一部分,为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量与用于解题的时间之间的函数关系式;
(2)求小迪回顾反思的学习收益量与用于回顾反思的时间的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
参考答案
1.B
2.C
3.A
4.D
5.B
6.A
7.D
8.A
9.A
10.A
11.,
12.
13.或
14.
15.
16.
17.
18.①②③④
19.
20.
21.,,,,,;理由略.
22.图象经过、两点的二次函数为; 点的坐标是或; 略.
23.反比例函数的解析式为; .
24.或;时,四边形为矩形;(3)当或时,以,,为顶点的三角形与相似.
25.(1)证明略;(2)CF=5.
26.解:(1)由图1,设.当时,,
解得,.
(2)由图2,当时,设.
当时,,
.
.
,即.
当时,.
因此
(3)设小迪用于回顾反思的时间为分钟,
学习收益总量为,则她用于解题的时间为分钟.
当时,.
当时,.
当时,.
随的增大而减小,因此当时,.
综上,当时,,此时.
答:小迪用于回顾反思的时间为3分钟,用于解题的时间为17分钟时,学习收益总量最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
