人教版四年级下册数学《三角形的内角和》课件(共18张PPT)
文档属性
| 名称 | 人教版四年级下册数学《三角形的内角和》课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 09:50:33 | ||
图片预览


文档简介
(共18张PPT)
三角形的内角和
三角形
人教版四年级下册
学 习 目 标:
1.通过测量、撕拼等方法,探索和发现三角形三个内角的和的度数。
2.会利用三角形的内角和求未知角的度数。
3.能在知识应用的过程中,能力得到进一步的发展。
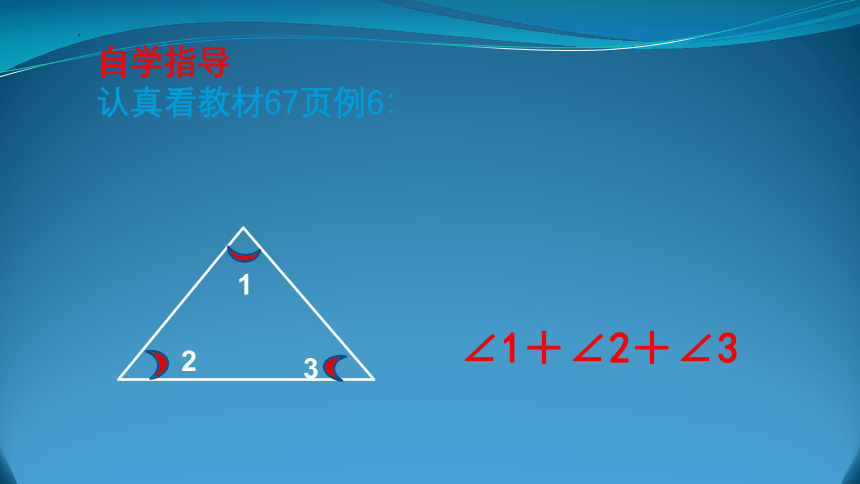
自学指导
认真看教材67页例6:
1
2
3
∠1+∠2+∠3
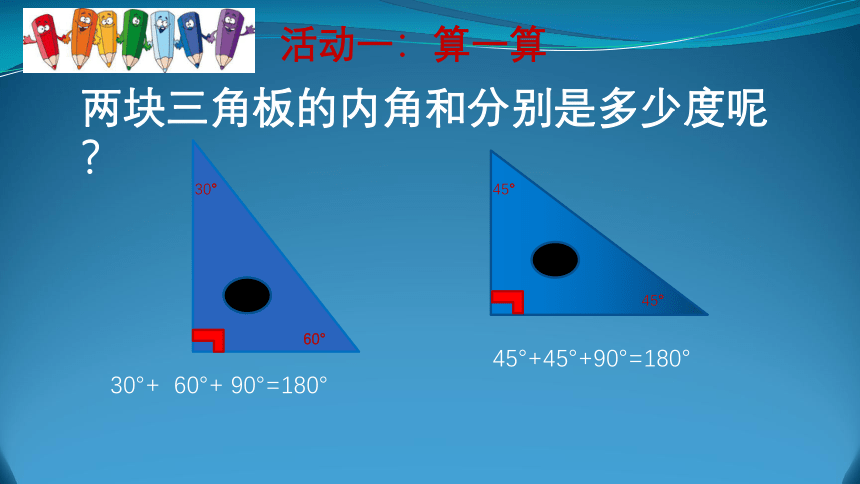
活动一:算一算
两块三角板的内角和分别是多少度呢?
30°
60°
45°
45°
30°+ 60°+ 90°=180°
45°+45°+90°=180°
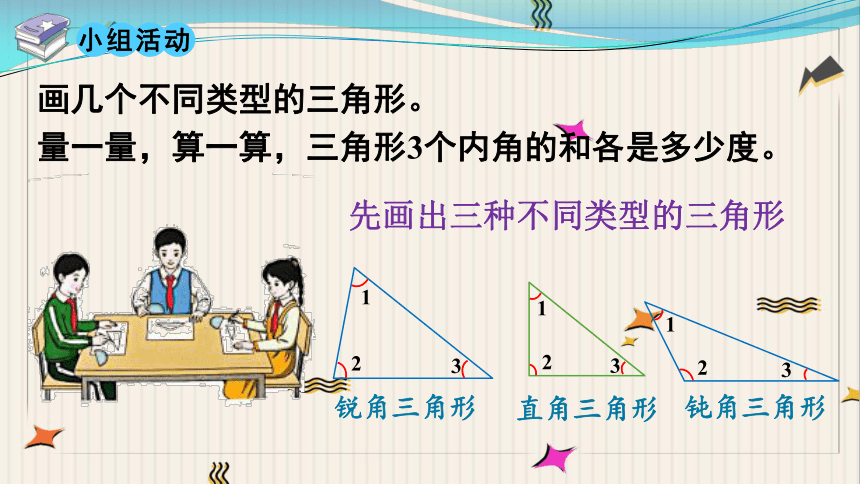
小组活动
画几个不同类型的三角形。
量一量,算一算,三角形3个内角的和各是多少度。
先画出三种不同类型的三角形
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
1
2
3
锐角三角形
1
2
3
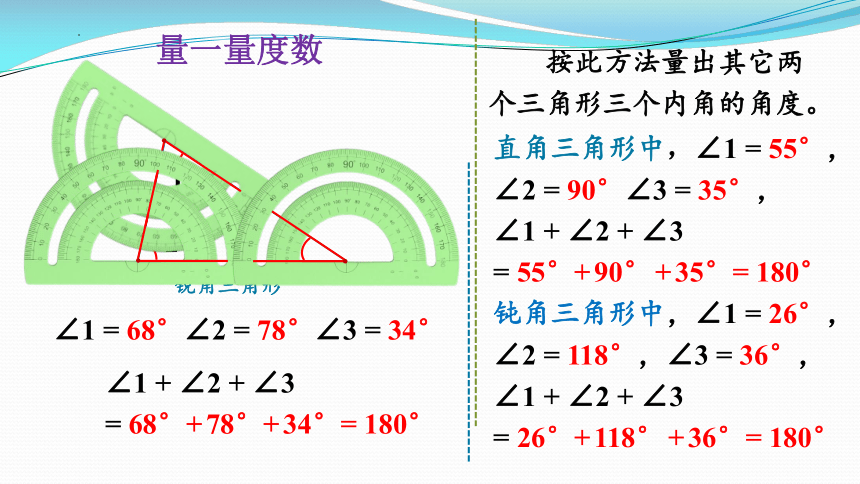
量一量度数
∠1=68°
∠2=78°
∠3=34°
按此方法量出其它两个三角形三个内角的角度。
∠1+∠2+∠3
=68°+78°+34°=180°
直角三角形中,∠1=55°,∠2=90°∠3=35°,
∠1+∠2+∠3
=55°+90°+35°=180°
钝角三角形中,∠1=26°,∠2=118°,∠3=36°,∠1+∠2+∠3
=26°+118°+36°=180°
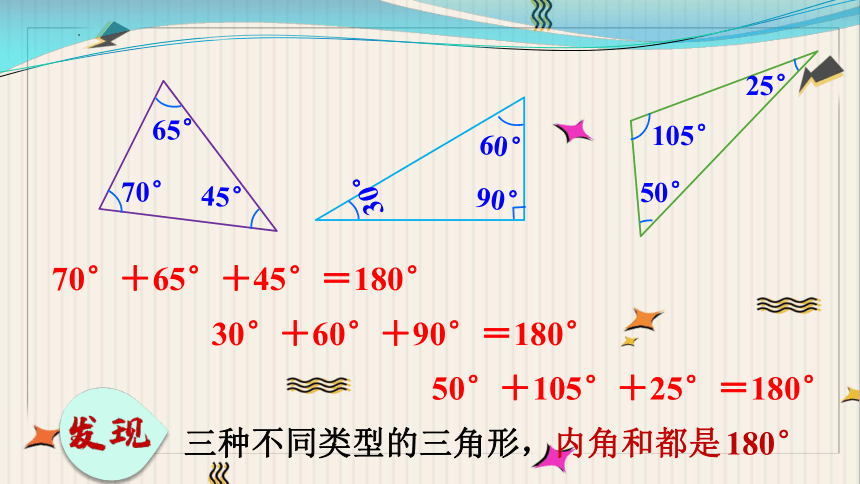
65°
70°
45°
105°
25°
50°
30°
90°
60°
70°+65°+45°=180°
30°+60°+90°=180°
50°+105°+25°=180°
三种不同类型的三角形,内角和都是180°
3、这三个角拼合在一起正好组成一个平角,即180°
活动二:拼一拼
1
2
3
3
1
2
1、把三角形的三个角撕下来。
2、把撕下来的这三个角的顶点重合、相邻边重合,拼在一起。
还有别的方法吗?
活动三:折一折:
2
2
1
1
3
3
三角形的内角和是180°。
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
1
2
3
☆三角形的内角和与三角形的大小和形状无关,是三角形的一种本质属性,任意一个三角形的内角和都是180°。
巩固运用
1.算出下面各个未知角的度数。
180°- 65°- 37°=78°
180°-90°- 30°=60°
180°- 25°- 20°=135°
2.填空题。
1)一个三角形最多有( )个锐角,最
少有( )个锐角。
2)任意一个三角形的内角和都是( )。
3)一个等腰三角形的一个底角是30°,另
外两个角分别是( )和( )。
3
2
180°
30°
120°
3.求出下列三角形各个角的度数。
每个角都是60°。
三个角的度数分别是96°、42°、42°。
三个角的度数分别是90°、40°、50°。
(3)一个直角三角形,其中一个锐角是40°。
(1)一个等边三角形。
(2)一个等腰三角形,顶角是96°。
4.爸爸给小红买了一个
等腰三角形的风筝。
风筝的一个底角是70°,
风筝的顶角是多少度?
答:它的顶角是40°。
180° 70° 70=40°
5.已知∠1、∠2、∠3是同一个三角形的三个
内角。
1)若∠1 =34°, ∠2=48°,则∠3=( )。
2)若∠1 =46°, ∠3=96°,则∠2=( )。
3)若∠3 =27°, ∠2=63°,则∠1=( )。
98°
38°
90°
6.猜一猜。
提示:另两个角的和为90°。
(1)
在三角形中,一个角是直角,另外两个角可能各是多少?
三角形的两条边分别是3cm和4cm,另一条边可能是多少厘米(取整厘米数)?
(2)
提示:另一条边的长必须大于1cm,小于7cm。
拓展运用
观察下图,求∠A和∠B的度数。(单位:cm)
解析:由图可知三角形BCD是等边三角形,三角形ACD是等腰三角形。
∠B=60°
180°-60°=120°
∠A=(180°-120°)÷2=30°
等边三角形的三个角都是60°。
同学们,下节课见!
三角形的内角和
三角形
人教版四年级下册
学 习 目 标:
1.通过测量、撕拼等方法,探索和发现三角形三个内角的和的度数。
2.会利用三角形的内角和求未知角的度数。
3.能在知识应用的过程中,能力得到进一步的发展。
自学指导
认真看教材67页例6:
1
2
3
∠1+∠2+∠3
活动一:算一算
两块三角板的内角和分别是多少度呢?
30°
60°
45°
45°
30°+ 60°+ 90°=180°
45°+45°+90°=180°
小组活动
画几个不同类型的三角形。
量一量,算一算,三角形3个内角的和各是多少度。
先画出三种不同类型的三角形
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
1
2
3
锐角三角形
1
2
3
量一量度数
∠1=68°
∠2=78°
∠3=34°
按此方法量出其它两个三角形三个内角的角度。
∠1+∠2+∠3
=68°+78°+34°=180°
直角三角形中,∠1=55°,∠2=90°∠3=35°,
∠1+∠2+∠3
=55°+90°+35°=180°
钝角三角形中,∠1=26°,∠2=118°,∠3=36°,∠1+∠2+∠3
=26°+118°+36°=180°
65°
70°
45°
105°
25°
50°
30°
90°
60°
70°+65°+45°=180°
30°+60°+90°=180°
50°+105°+25°=180°
三种不同类型的三角形,内角和都是180°
3、这三个角拼合在一起正好组成一个平角,即180°
活动二:拼一拼
1
2
3
3
1
2
1、把三角形的三个角撕下来。
2、把撕下来的这三个角的顶点重合、相邻边重合,拼在一起。
还有别的方法吗?
活动三:折一折:
2
2
1
1
3
3
三角形的内角和是180°。
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
1
2
3
☆三角形的内角和与三角形的大小和形状无关,是三角形的一种本质属性,任意一个三角形的内角和都是180°。
巩固运用
1.算出下面各个未知角的度数。
180°- 65°- 37°=78°
180°-90°- 30°=60°
180°- 25°- 20°=135°
2.填空题。
1)一个三角形最多有( )个锐角,最
少有( )个锐角。
2)任意一个三角形的内角和都是( )。
3)一个等腰三角形的一个底角是30°,另
外两个角分别是( )和( )。
3
2
180°
30°
120°
3.求出下列三角形各个角的度数。
每个角都是60°。
三个角的度数分别是96°、42°、42°。
三个角的度数分别是90°、40°、50°。
(3)一个直角三角形,其中一个锐角是40°。
(1)一个等边三角形。
(2)一个等腰三角形,顶角是96°。
4.爸爸给小红买了一个
等腰三角形的风筝。
风筝的一个底角是70°,
风筝的顶角是多少度?
答:它的顶角是40°。
180° 70° 70=40°
5.已知∠1、∠2、∠3是同一个三角形的三个
内角。
1)若∠1 =34°, ∠2=48°,则∠3=( )。
2)若∠1 =46°, ∠3=96°,则∠2=( )。
3)若∠3 =27°, ∠2=63°,则∠1=( )。
98°
38°
90°
6.猜一猜。
提示:另两个角的和为90°。
(1)
在三角形中,一个角是直角,另外两个角可能各是多少?
三角形的两条边分别是3cm和4cm,另一条边可能是多少厘米(取整厘米数)?
(2)
提示:另一条边的长必须大于1cm,小于7cm。
拓展运用
观察下图,求∠A和∠B的度数。(单位:cm)
解析:由图可知三角形BCD是等边三角形,三角形ACD是等腰三角形。
∠B=60°
180°-60°=120°
∠A=(180°-120°)÷2=30°
等边三角形的三个角都是60°。
同学们,下节课见!
