1.2 一定是直角三角形吗同步练习2023—2024学年北师大版数学八年级上册(含答案)
文档属性
| 名称 | 1.2 一定是直角三角形吗同步练习2023—2024学年北师大版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 481.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 14:03:20 | ||
图片预览

文档简介
1.2 一定是直角三角形吗 同步练习
一、单选题
1.如图,已知钓鱼竿的长为,露在水面上的鱼线长为,某钓者想看看鱼钩上的情况,把鱼竿转动到的位置,此时露在水面上的鱼线为,则的长为( )
A. B. C. D.
2.如图,圆柱的底面周长是14cm,圆柱高为24cm,一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B,那么它爬行的最短路程为( )
A.14cm B.15cm C.24cm D.25cm
3.为预防新冠疫情,民生大院入口的正上方处装有红外线激光测温仪(如图所示),测温仪离地面的距离米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为米的市民正对门缓慢走到离门米的地方时(即米),测温仪自动显示体温,则人头顶离测温仪的距离等于( )
A.米 B.米 C.米 D.米
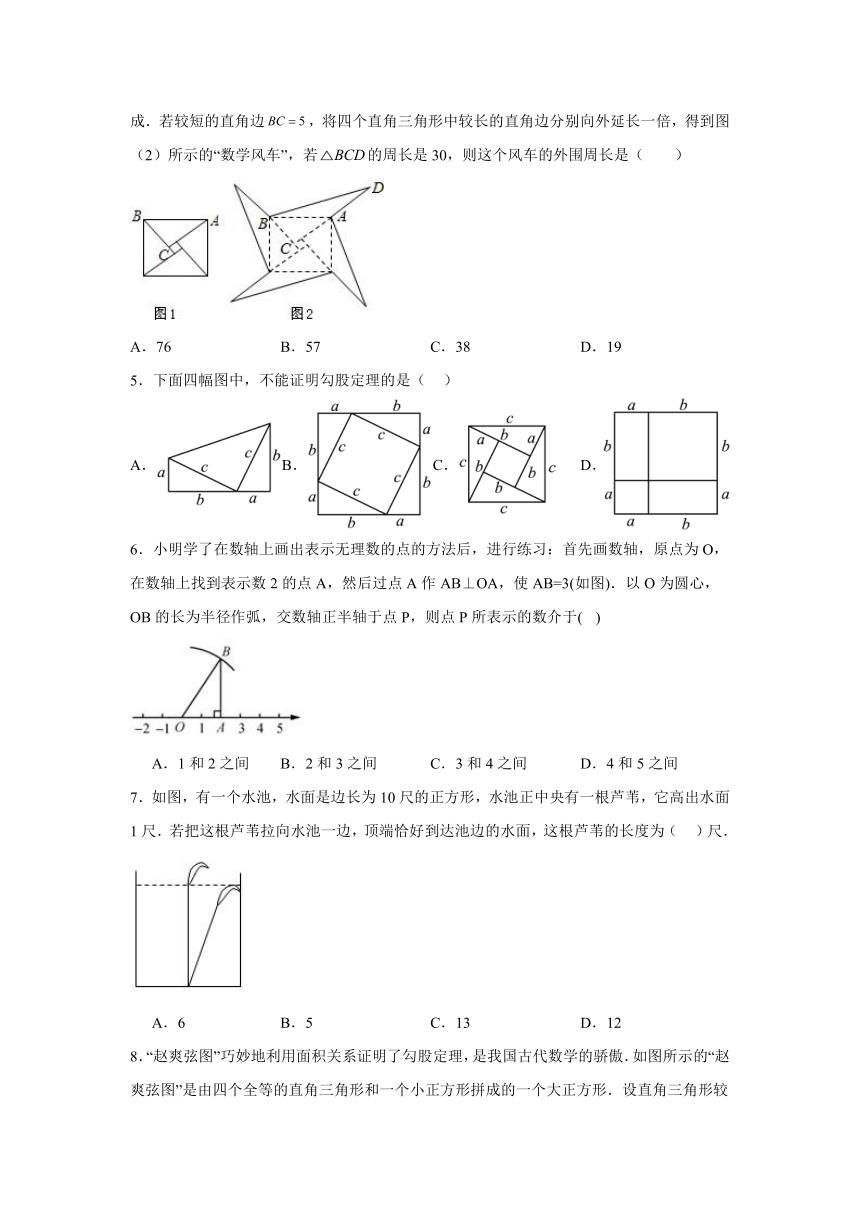
4.如图,图(1)是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边,将四个直角三角形中较长的直角边分别向外延长一倍,得到图(2)所示的“数学风车”,若的周长是30,则这个风车的外围周长是( )
A.76 B.57 C.38 D.19
5.下面四幅图中,不能证明勾股定理的是( )
A.B.C. D.
6.小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3(如图).以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,则点P所表示的数介于( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
7.如图,有一个水池,水面是边长为10尺的正方形,水池正中央有一根芦苇,它高出水面1尺.若把这根芦苇拉向水池一边,顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.6 B.5 C.13 D.12
8.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为
A.9 B.6 C.4 D.3
二、填空题
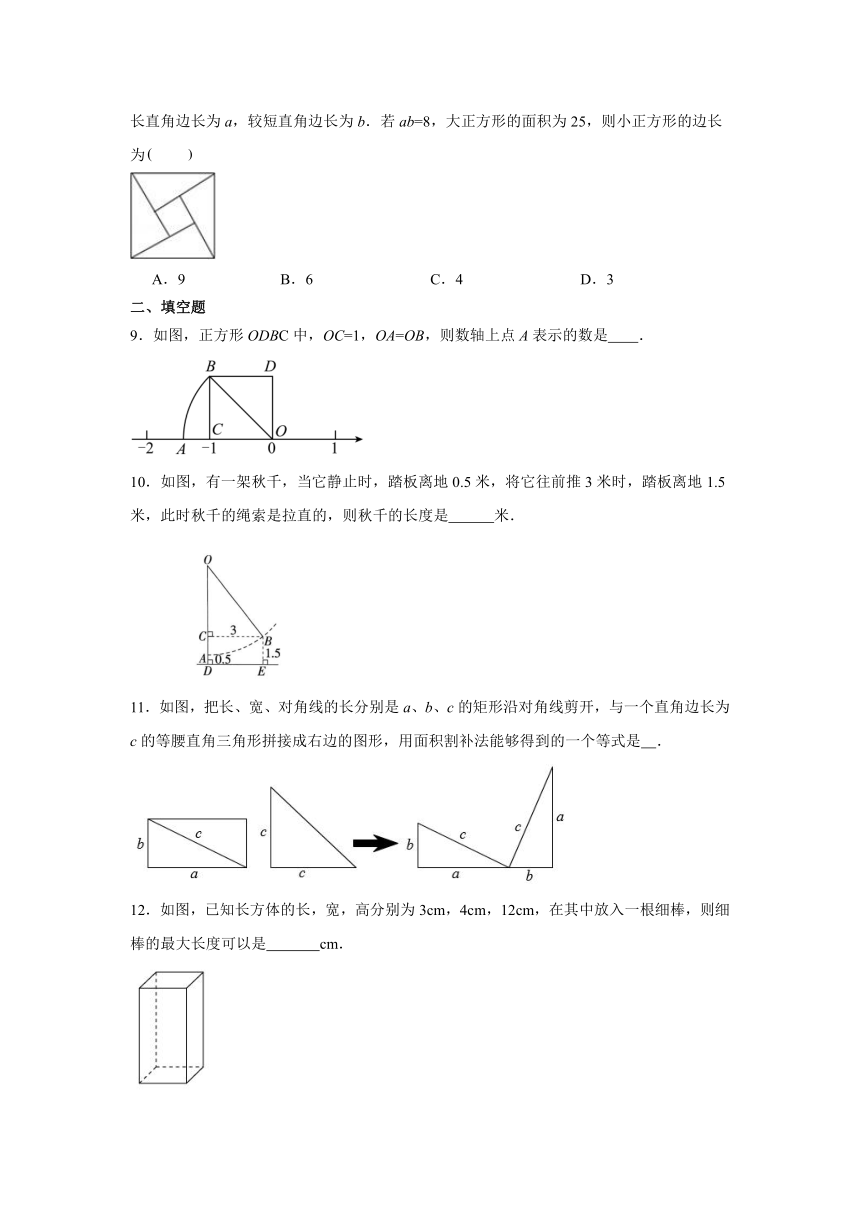
9.如图,正方形ODBC中,OC=1,OA=OB,则数轴上点A表示的数是 .
10.如图,有一架秋千,当它静止时,踏板离地0.5米,将它往前推3米时,踏板离地1.5米,此时秋千的绳索是拉直的,则秋千的长度是 米.
11.如图,把长、宽、对角线的长分别是a、b、c的矩形沿对角线剪开,与一个直角边长为c的等腰直角三角形拼接成右边的图形,用面积割补法能够得到的一个等式是 .
12.如图,已知长方体的长,宽,高分别为3cm,4cm,12cm,在其中放入一根细棒,则细棒的最大长度可以是 cm.
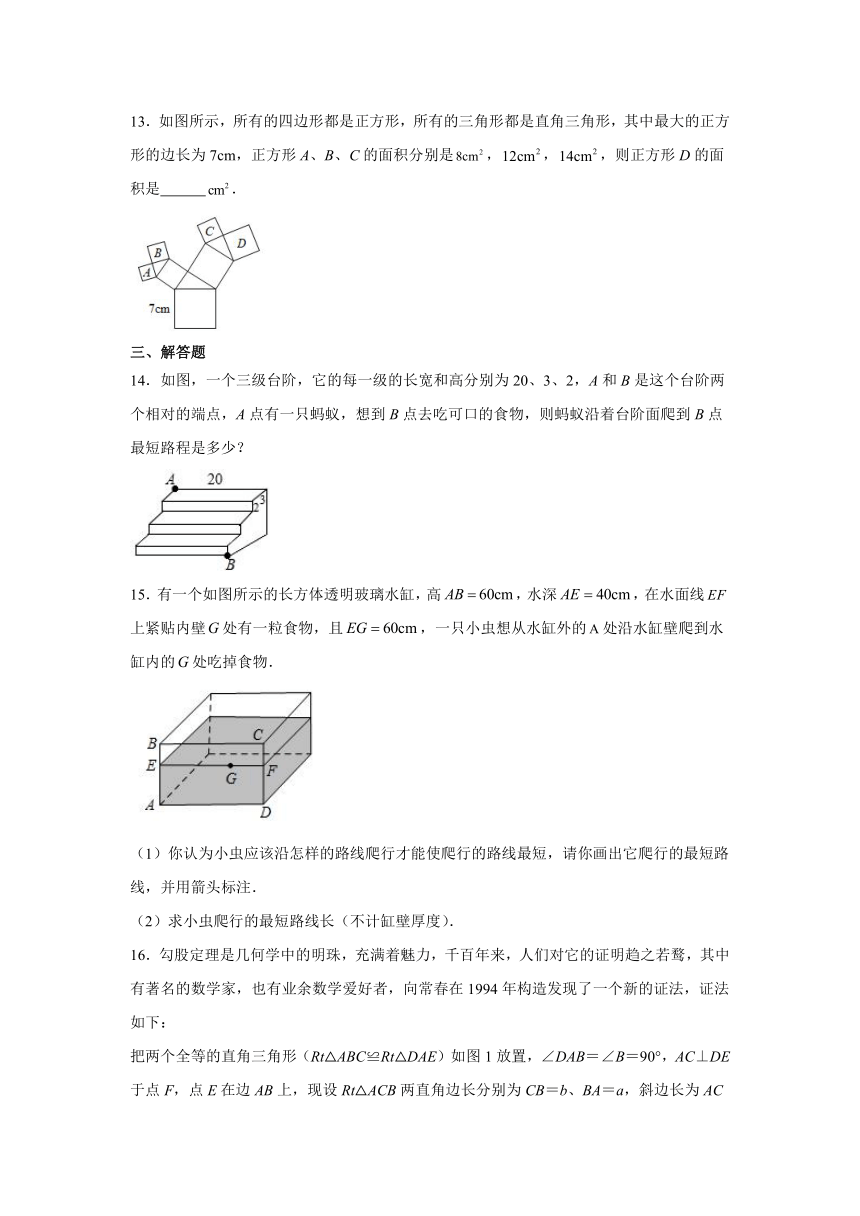
13.如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形A、B、C的面积分别是,,,则正方形D的面积是 .
三、解答题
14.如图,一个三级台阶,它的每一级的长宽和高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
15.有一个如图所示的长方体透明玻璃水缸,高,水深,在水面线上紧贴内壁处有一粒食物,且,一只小虫想从水缸外的处沿水缸壁爬到水缸内的处吃掉食物.
(1)你认为小虫应该沿怎样的路线爬行才能使爬行的路线最短,请你画出它爬行的最短路线,并用箭头标注.
(2)求小虫爬行的最短路线长(不计缸壁厚度).
16.勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法,证法如下:
把两个全等的直角三角形(Rt△ABC≌Rt△DAE)如图1放置,∠DAB=∠B=90°,AC⊥DE于点F,点E在边AB上,现设Rt△ACB两直角边长分别为CB=b、BA=a,斜边长为AC=c,请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为多少千米.
17.如图,地面上放着一个小凳子(与地面平行),点A到墙面(墙面与地面垂直)的距离为.在图①中,一木杆的一端与墙角O重合,另一端靠在点A处,.
(1)求小凳子的高度;
(2)在图②中另一木杆的一端与点B重合,另一端靠在墙上的点C处.若,木杆比凳宽长,求小凳子宽和木杆的长度.
参考答案
1--8BDAAD CCD
9.
10.5
11.a2+b2=c2
12.13
13.15
14.解:如图所示,
∵三级台阶平面展开图为长方形,长为20,宽为(2+3)×3=15,
∴蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长,
由勾股定理得:,
则蚂蚁沿着台阶面爬到B点最短路程是25.
15.解:(1)如下图所示,
作点A关于BC所在直线的对称点,连接,与交于点,
由两点之间线段最短,此时A’G最短,
则为最短路线.
(2)∵,
∴,
∴.
在中,,,
∴.
由对称性可知,
∴.
故小虫爬行的最短路线长为100cm.
16.(1)解:∵S梯形ABCD=a(a+b),S△EBC=b(a-b),S四边形AECD=c2,
它们满足的关系式为:a(a+b)=b(a-b)+c2,
即a2+b2=c2;
(2)解:如图2①,连接CD,作CE⊥AD于点E,
∵AD⊥AB,BC⊥AB,
∴BC=AE,CE=AB,
∴DE=AD-AE=25-16=9千米,
∴CD= =41(千米),
∴两个村庄相距41千米.
17.(1)解:过A作垂直于墙面,垂足M,
根据题意可得,,
在中,,
即凳子的高度为.
(2)解:延长交墙面于点N,可得,
设cm,则,,,
在中,,即,
解得,则.
一、单选题
1.如图,已知钓鱼竿的长为,露在水面上的鱼线长为,某钓者想看看鱼钩上的情况,把鱼竿转动到的位置,此时露在水面上的鱼线为,则的长为( )
A. B. C. D.
2.如图,圆柱的底面周长是14cm,圆柱高为24cm,一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B,那么它爬行的最短路程为( )
A.14cm B.15cm C.24cm D.25cm
3.为预防新冠疫情,民生大院入口的正上方处装有红外线激光测温仪(如图所示),测温仪离地面的距离米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为米的市民正对门缓慢走到离门米的地方时(即米),测温仪自动显示体温,则人头顶离测温仪的距离等于( )
A.米 B.米 C.米 D.米
4.如图,图(1)是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边,将四个直角三角形中较长的直角边分别向外延长一倍,得到图(2)所示的“数学风车”,若的周长是30,则这个风车的外围周长是( )
A.76 B.57 C.38 D.19
5.下面四幅图中,不能证明勾股定理的是( )
A.B.C. D.
6.小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3(如图).以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,则点P所表示的数介于( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
7.如图,有一个水池,水面是边长为10尺的正方形,水池正中央有一根芦苇,它高出水面1尺.若把这根芦苇拉向水池一边,顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.6 B.5 C.13 D.12
8.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为
A.9 B.6 C.4 D.3
二、填空题
9.如图,正方形ODBC中,OC=1,OA=OB,则数轴上点A表示的数是 .
10.如图,有一架秋千,当它静止时,踏板离地0.5米,将它往前推3米时,踏板离地1.5米,此时秋千的绳索是拉直的,则秋千的长度是 米.
11.如图,把长、宽、对角线的长分别是a、b、c的矩形沿对角线剪开,与一个直角边长为c的等腰直角三角形拼接成右边的图形,用面积割补法能够得到的一个等式是 .
12.如图,已知长方体的长,宽,高分别为3cm,4cm,12cm,在其中放入一根细棒,则细棒的最大长度可以是 cm.
13.如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形A、B、C的面积分别是,,,则正方形D的面积是 .
三、解答题
14.如图,一个三级台阶,它的每一级的长宽和高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
15.有一个如图所示的长方体透明玻璃水缸,高,水深,在水面线上紧贴内壁处有一粒食物,且,一只小虫想从水缸外的处沿水缸壁爬到水缸内的处吃掉食物.
(1)你认为小虫应该沿怎样的路线爬行才能使爬行的路线最短,请你画出它爬行的最短路线,并用箭头标注.
(2)求小虫爬行的最短路线长(不计缸壁厚度).
16.勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法,证法如下:
把两个全等的直角三角形(Rt△ABC≌Rt△DAE)如图1放置,∠DAB=∠B=90°,AC⊥DE于点F,点E在边AB上,现设Rt△ACB两直角边长分别为CB=b、BA=a,斜边长为AC=c,请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为多少千米.
17.如图,地面上放着一个小凳子(与地面平行),点A到墙面(墙面与地面垂直)的距离为.在图①中,一木杆的一端与墙角O重合,另一端靠在点A处,.
(1)求小凳子的高度;
(2)在图②中另一木杆的一端与点B重合,另一端靠在墙上的点C处.若,木杆比凳宽长,求小凳子宽和木杆的长度.
参考答案
1--8BDAAD CCD
9.
10.5
11.a2+b2=c2
12.13
13.15
14.解:如图所示,
∵三级台阶平面展开图为长方形,长为20,宽为(2+3)×3=15,
∴蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长,
由勾股定理得:,
则蚂蚁沿着台阶面爬到B点最短路程是25.
15.解:(1)如下图所示,
作点A关于BC所在直线的对称点,连接,与交于点,
由两点之间线段最短,此时A’G最短,
则为最短路线.
(2)∵,
∴,
∴.
在中,,,
∴.
由对称性可知,
∴.
故小虫爬行的最短路线长为100cm.
16.(1)解:∵S梯形ABCD=a(a+b),S△EBC=b(a-b),S四边形AECD=c2,
它们满足的关系式为:a(a+b)=b(a-b)+c2,
即a2+b2=c2;
(2)解:如图2①,连接CD,作CE⊥AD于点E,
∵AD⊥AB,BC⊥AB,
∴BC=AE,CE=AB,
∴DE=AD-AE=25-16=9千米,
∴CD= =41(千米),
∴两个村庄相距41千米.
17.(1)解:过A作垂直于墙面,垂足M,
根据题意可得,,
在中,,
即凳子的高度为.
(2)解:延长交墙面于点N,可得,
设cm,则,,,
在中,,即,
解得,则.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
