26.1 反比例函数 同步练习 人教版数学九年级下册(含答案)
文档属性
| 名称 | 26.1 反比例函数 同步练习 人教版数学九年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 150.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 14:11:50 | ||
图片预览


文档简介
26.1 反比例函数 同步练习 2022-2023学年人教版数学九年级下册
一、单选题
1.二次函数与反比例函数的交点个数为( ).
A.1 B.2 C.3 D.0
2.下列函数中,图象经过点(2,﹣3)的反比例函数关系式是( )
A.y=- B.y= C.y= D.y=-
3.若反比例函数y= (k≠0)的图象经过P(﹣2,3),则该函数不经过的图象的点是( )
A.(3,﹣2) B.(1,﹣6)
C.(﹣1,6) D.(﹣1,﹣6)
4.已知反比例函数 ,下列结论中错误的是
A.其图象经过点
B.其图象分别位于第一、第三象限
C.当 时,y随x的增大而减小
D.当 时,
5.点A(x1,y1),B(x2,y2)都在反比例函数 的图象上,若x1<x2<0,则( )
A.y2>y1>0 B.y1>y2>0 C.y2<y1<0 D.y1<y2<0
6.如图,□ABCD的顶点A的坐标为( ),顶点D在双曲线y= (x>0), AD交y轴于点E(0,2),且四边形BCDE的面积是△ABE面积的3倍,则k的值为 ( )
A.4 B.6 C.7 D.8
7.小明同学利用计算机软件绘制函数 (a、b为常数)的图象如图所示,由学习函数的经验,可以推断常数a、b的值满足( )
A. , B. ,
C. , D. ,
8.如图,点 和点 分别是反比例函数 和 的图像上的点, 轴,点 为 轴上一点,若 ,则 的值为( )
A.2 B.4 C.6 D.8
二、填空题
9.反比例函数 的图像经过 , 两点,其中 ,且 ,则 的范围是 .
10.如图,M为双曲线y= 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD BC的值为 .
11.已知点A在反比例函数 的图象上,AB⊥y轴,点C在x轴上,S△ABC=2,则反比例函数的解析式为 .
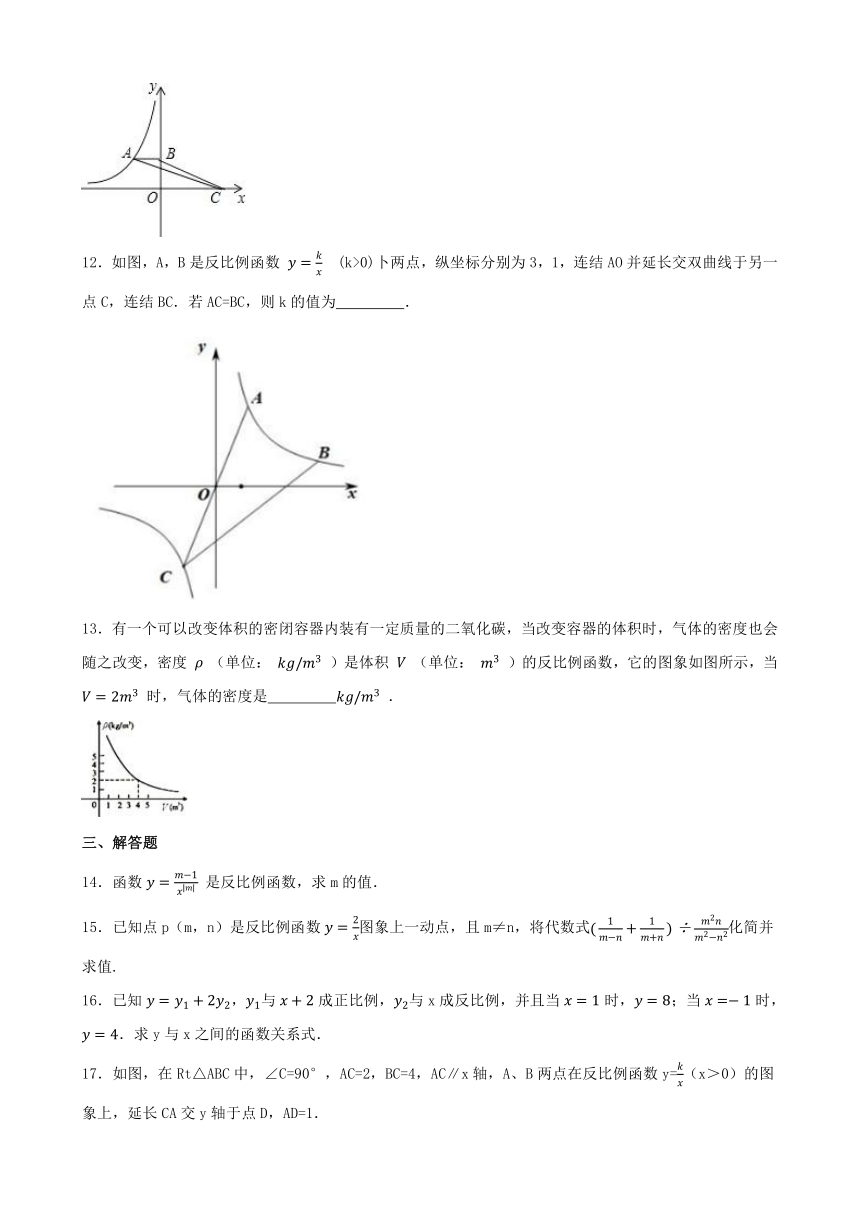
12.如图,A,B是反比例函数 (k>0)卜两点,纵坐标分别为3,1,连结AO并延长交双曲线于另一点C,连结BC.若AC=BC,则k的值为 .
13.有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )是体积 (单位: )的反比例函数,它的图象如图所示,当 时,气体的密度是 .
三、解答题
14.函数 是反比例函数,求m的值.
15.已知点p(m,n)是反比例函数图象上一动点,且m≠n,将代数式化简并求值.
16.已知,与成正比例,与x成反比例,并且当时,;当时,.求y与x之间的函数关系式.
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=(x>0)的图象上,延长CA交y轴于点D,AD=1.
(1)求该反比例函数的解析式;
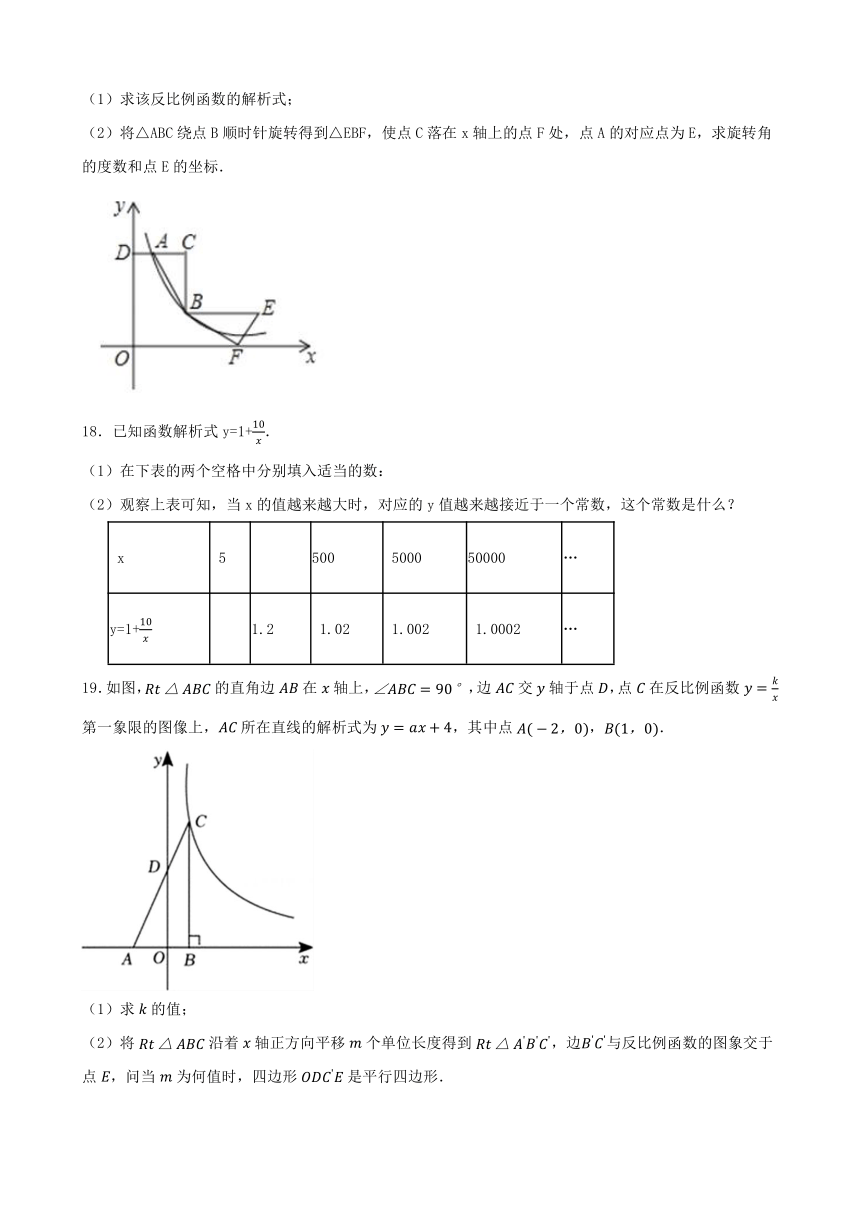
(2)将△ABC绕点B顺时针旋转得到△EBF,使点C落在x轴上的点F处,点A的对应点为E,求旋转角的度数和点E的坐标.
18.已知函数解析式y=1+.
(1)在下表的两个空格中分别填入适当的数:
(2)观察上表可知,当x的值越来越大时,对应的y值越来越接近于一个常数,这个常数是什么?
x 5
500 5000 50000 …
y=1+
1.2 1.02 1.002 1.0002 …
19.如图,的直角边在轴上,,边交轴于点,点在反比例函数第一象限的图像上,所在直线的解析式为,其中点,.
(1)求的值;
(2)将沿着轴正方向平移个单位长度得到,边与反比例函数的图象交于点,问当为何值时,四边形是平行四边形.
参考答案
1.A
2.D
3.D
4.D
5.C
6.B
7.C
8.A
9.k<1
10.2
11.y=﹣
12.
13.4
14.解:根据题意得m﹣1≠0且|m|=1,
解得m=﹣1.
15.解:∵点p(m,n)是反比例函数图象上一动点,
∴mn=2,
∵m≠n,
∴m﹣n≠0,
==1.
16.解:与成正比例,
设,,
与x成反比例,
设
,
把,和,代入得:
,
解得:,
,
答:y与x之间的函数关系式是.
17.解:(1)∵AC∥x轴,AD=1,
∴A(1,k),
∵∠C=90°,AC=2,BC=4,
∴B(3,k﹣4),
∵点B在y=的图象上,
∴3(k﹣4)=k,解得k=6,
∴该反比例函数的解析式为y=;
(2)作BM⊥x轴于M,EN⊥x轴于N,如图,
∵△ABC绕点B顺时针旋转得到△EBF,
∴BF=BC=4,EF=AC=2,∠BFE=∠BCA=90°,∠CBF等于旋转角,
∵BC⊥x轴,A(1,6),
∴BM=CM﹣BC=6﹣4=2,
在Rt△BMF中,∵cos∠MBF===,
∴∠MBF=60°,MF=BM=2,
∴∠CBF=180°﹣∠MBF=120°,
∴旋转角为120°;
∵∠BFM+∠MBF=90°,∠BFM+∠EFN=90°,
∴∠MBF=∠EFN,
∴Rt△BMF∽Rt△FNE,
∴==,即==,
∴FN=1,EN=,
∴ON=OM+MF+FN=3+2+1=4+,
∴E点坐标为(4+2,).
18.解:(1)x=5时,y=3;y=1.2时,x=50;
填入表格如下:
x 5 50 500 5000 50000 …
y=1+ 3 1.2 1.02 1.002 1.0002 …
(2)由上表可知,当x的值越来越大时,对应的y值越来越接近于常数1.
19.(1)解:∵直线:经过点,
∴,
∴,
∴所在直线的解析式为,
∵,,
∴当时,,
∴,,
∵点在反比例函数第一象限的图像上,
∴,
∴的值为.
(2)解:当时,,
∴,,
∵沿着轴正方向平移个单位长度得到,
∴,,,
∴当时,四边形是平行四边形,
由(1)得反比例函数的解析式为,
由题意可得点的横坐标为,
∴点的纵坐标,
∴,
解得:,且符合题意;
∴当为时,四边形是平行四边形.
一、单选题
1.二次函数与反比例函数的交点个数为( ).
A.1 B.2 C.3 D.0
2.下列函数中,图象经过点(2,﹣3)的反比例函数关系式是( )
A.y=- B.y= C.y= D.y=-
3.若反比例函数y= (k≠0)的图象经过P(﹣2,3),则该函数不经过的图象的点是( )
A.(3,﹣2) B.(1,﹣6)
C.(﹣1,6) D.(﹣1,﹣6)
4.已知反比例函数 ,下列结论中错误的是
A.其图象经过点
B.其图象分别位于第一、第三象限
C.当 时,y随x的增大而减小
D.当 时,
5.点A(x1,y1),B(x2,y2)都在反比例函数 的图象上,若x1<x2<0,则( )
A.y2>y1>0 B.y1>y2>0 C.y2<y1<0 D.y1<y2<0
6.如图,□ABCD的顶点A的坐标为( ),顶点D在双曲线y= (x>0), AD交y轴于点E(0,2),且四边形BCDE的面积是△ABE面积的3倍,则k的值为 ( )
A.4 B.6 C.7 D.8
7.小明同学利用计算机软件绘制函数 (a、b为常数)的图象如图所示,由学习函数的经验,可以推断常数a、b的值满足( )
A. , B. ,
C. , D. ,
8.如图,点 和点 分别是反比例函数 和 的图像上的点, 轴,点 为 轴上一点,若 ,则 的值为( )
A.2 B.4 C.6 D.8
二、填空题
9.反比例函数 的图像经过 , 两点,其中 ,且 ,则 的范围是 .
10.如图,M为双曲线y= 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD BC的值为 .
11.已知点A在反比例函数 的图象上,AB⊥y轴,点C在x轴上,S△ABC=2,则反比例函数的解析式为 .
12.如图,A,B是反比例函数 (k>0)卜两点,纵坐标分别为3,1,连结AO并延长交双曲线于另一点C,连结BC.若AC=BC,则k的值为 .
13.有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )是体积 (单位: )的反比例函数,它的图象如图所示,当 时,气体的密度是 .
三、解答题
14.函数 是反比例函数,求m的值.
15.已知点p(m,n)是反比例函数图象上一动点,且m≠n,将代数式化简并求值.
16.已知,与成正比例,与x成反比例,并且当时,;当时,.求y与x之间的函数关系式.
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=(x>0)的图象上,延长CA交y轴于点D,AD=1.
(1)求该反比例函数的解析式;
(2)将△ABC绕点B顺时针旋转得到△EBF,使点C落在x轴上的点F处,点A的对应点为E,求旋转角的度数和点E的坐标.
18.已知函数解析式y=1+.
(1)在下表的两个空格中分别填入适当的数:
(2)观察上表可知,当x的值越来越大时,对应的y值越来越接近于一个常数,这个常数是什么?
x 5
500 5000 50000 …
y=1+
1.2 1.02 1.002 1.0002 …
19.如图,的直角边在轴上,,边交轴于点,点在反比例函数第一象限的图像上,所在直线的解析式为,其中点,.
(1)求的值;
(2)将沿着轴正方向平移个单位长度得到,边与反比例函数的图象交于点,问当为何值时,四边形是平行四边形.
参考答案
1.A
2.D
3.D
4.D
5.C
6.B
7.C
8.A
9.k<1
10.2
11.y=﹣
12.
13.4
14.解:根据题意得m﹣1≠0且|m|=1,
解得m=﹣1.
15.解:∵点p(m,n)是反比例函数图象上一动点,
∴mn=2,
∵m≠n,
∴m﹣n≠0,
==1.
16.解:与成正比例,
设,,
与x成反比例,
设
,
把,和,代入得:
,
解得:,
,
答:y与x之间的函数关系式是.
17.解:(1)∵AC∥x轴,AD=1,
∴A(1,k),
∵∠C=90°,AC=2,BC=4,
∴B(3,k﹣4),
∵点B在y=的图象上,
∴3(k﹣4)=k,解得k=6,
∴该反比例函数的解析式为y=;
(2)作BM⊥x轴于M,EN⊥x轴于N,如图,
∵△ABC绕点B顺时针旋转得到△EBF,
∴BF=BC=4,EF=AC=2,∠BFE=∠BCA=90°,∠CBF等于旋转角,
∵BC⊥x轴,A(1,6),
∴BM=CM﹣BC=6﹣4=2,
在Rt△BMF中,∵cos∠MBF===,
∴∠MBF=60°,MF=BM=2,
∴∠CBF=180°﹣∠MBF=120°,
∴旋转角为120°;
∵∠BFM+∠MBF=90°,∠BFM+∠EFN=90°,
∴∠MBF=∠EFN,
∴Rt△BMF∽Rt△FNE,
∴==,即==,
∴FN=1,EN=,
∴ON=OM+MF+FN=3+2+1=4+,
∴E点坐标为(4+2,).
18.解:(1)x=5时,y=3;y=1.2时,x=50;
填入表格如下:
x 5 50 500 5000 50000 …
y=1+ 3 1.2 1.02 1.002 1.0002 …
(2)由上表可知,当x的值越来越大时,对应的y值越来越接近于常数1.
19.(1)解:∵直线:经过点,
∴,
∴,
∴所在直线的解析式为,
∵,,
∴当时,,
∴,,
∵点在反比例函数第一象限的图像上,
∴,
∴的值为.
(2)解:当时,,
∴,,
∵沿着轴正方向平移个单位长度得到,
∴,,,
∴当时,四边形是平行四边形,
由(1)得反比例函数的解析式为,
由题意可得点的横坐标为,
∴点的纵坐标,
∴,
解得:,且符合题意;
∴当为时,四边形是平行四边形.
