数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
2.2.3 直线的一般式方程
学习目标
素 养 目 标 学 科 素 养
1.掌握直线的一般式方程(重点). 2.理解关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示直线. 3.会进行直线方程的五种形式之间的转化(重、难点). 1、直观想象
2、数学运算
3、数形结合
复习回顾
问题1 :四种表示直线的方程,
点斜式方程 斜截式方程 两点式方程 截距式方程
它们有怎样的区别与联系呢?
区别:应用条件不同,表达形式不同;
( )
联系:
直线上任意点的几何特征
直线的代数表示:直线上的横纵坐标x,y的关系
形
数
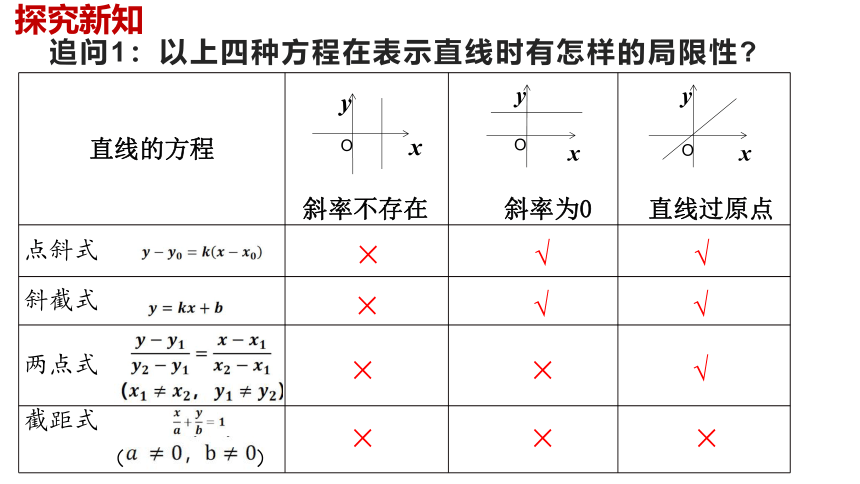
追问1:以上四种方程在表示直线时有怎样的局限性
直线的方程 斜率不存在 斜率为0
直线过原点
点斜式
斜截式
两点式
截距式 ( )
y
x
O
x
y
O
x
y
O
探究新知
× √ √
× √ √
× × √
× × ×
探究新知
探究一:直线的方程与二元一次方程的关系
探究二:直线的一般式方程的表达
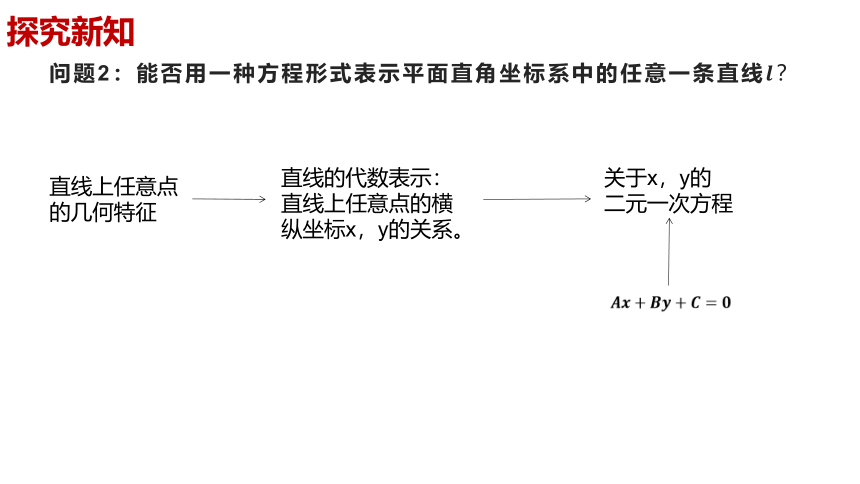
问题2:能否用一种方程形式表示平面直角坐标系中的任意一条直线
探究新知
直线上任意点
的几何特征
直线的代数表示:直线上任意点的横纵坐标x,y的关系。
关于x,y的
二元一次方程
追问1:在平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程 表示吗?
直线
斜率存在
斜率不存在
(A,B不同时为0)
探究新知
探究新知
追问2:对于任意一个关于,的二元一次方程(A,B不同时为0)是否都表示一条直线?
(A,B不同时为0)
B≠0
B=0
A≠0
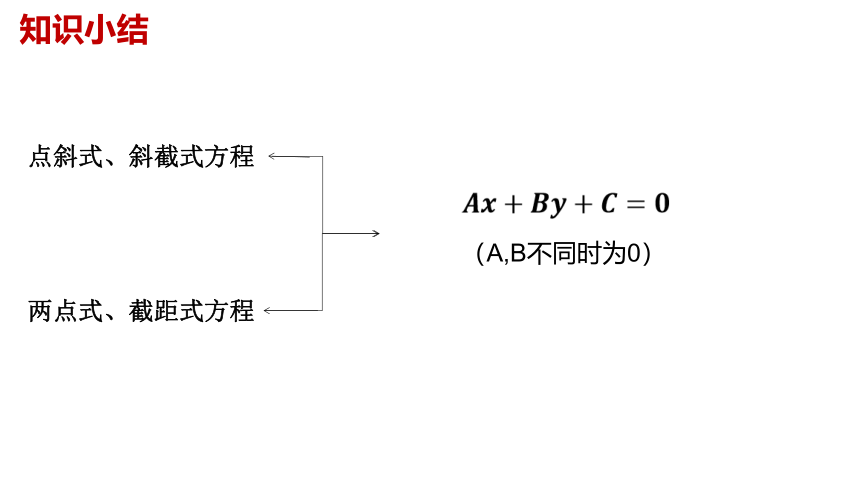
知识小结
点斜式、斜截式方程
两点式、截距式方程
(A,B不同时为0)
(A,B不同时为0)
知识小结
直线
平面直角坐标系
问题3: 在方程 中,A,B,C为何值时,方程表示的直线:
探究新知
(A,B不同时为0)
平行于x轴
x
y
O
斜率为0,
在y轴上截距不为0
A=0,B≠0
4.与y轴重合?
2.平行于y轴?
1.平行于x轴?
3.与x轴重合?
A=0
B≠0
C≠0
1.平行于x轴?
问题3: 在方程 中,A,B,C为何值时,方程表示的直线:
探究新知
(A,B不同时为0)
平行于y轴
斜率不存在,
在x轴上截距不为0
A≠0,B=0
4.与y轴重合?
2.平行于y轴?
1.平行于x轴?
3.与x轴重合?
A≠0
B=0
C≠0
2.平行于y轴?
y
x
O
问题3: 在方程 中,A,B,C为何值时,方程表示的直线:
探究新知
(A,B不同时为0)
与x轴重合
x
y
O
斜率为0,
在y轴上截距为0
A=0,B≠0
y=0
4.与y轴重合?
2.平行于y轴?
1.平行于x轴?
3.与x轴重合?
A=0
B≠0
C=0
3.与x轴重合?
问题3: 在方程 中,A,B,C为何值时,方程表示的直线:
探究新知
(A,B不同时为0)
与y轴重合
斜率不存在,
在x轴上截距为0
A≠0,B=0
x=0
4.与y轴重合?
2.平行于y轴?
1.平行于x轴?
3.与x轴重合?
A≠0
B=0
C=0
y
x
O
4.与y轴重合?
直线的方程 斜率不存在 斜率为0
直线过原点
点斜式 × √ √
× √ 斜截式 √
两点式 × × √
截距式 ( ) × × ×
(A,B不同时为0)
y
x
O
x
y
O
x
y
O
知识小结
√ √ √
随堂练习
例1 已知直线经过点A(6,4),斜率为,求直线的点斜式和一般式方程.
随堂练习
例2 把直线的一般式方程化为斜截式,求出直线的斜率以及它在轴与轴上的截距,并画出图形.
课堂总结
平面直角坐标系
直线
二元一次方程
(A,B不同时为0)
随堂练习
1.根据下列条件,写出直线的方程,并把它化为一般式:
(1)经过点,斜率是,
(2)经过点平行于轴;
(3)经过点,;
(4)在轴、 轴的截距分别是,3.
随堂练习
2.求下列直线的斜率以及在y轴上的截距,并画出图形:
(1); (2);
(3)x+2y=0; (4)7x 6y+4=0.
随堂练习
3.已知直线的方程是Ax+By+C=0.
(1)当B≠0时,直线的斜率是多少?当B=0时呢?
(2)系数取什么值时,方程表示经过原点的直线?
习题小结
求直线方程时方程形式的选择技巧
(1)已知一点的坐标,求过该点的直线方程时,通常选用点斜式方程.
(2)已知直线的斜率,通常选用点斜式或斜截式,再由其他条件确定一个定点的坐标或在y轴上的截距.
(3)已知直线在两坐标轴上的截距时,通常选用截距式方程.
(4)已知直线上两点时,通常选用两点式方程.
不管黑猫白猫,抓到老鼠就是好猫!
2.2.3 直线的一般式方程
学习目标
素 养 目 标 学 科 素 养
1.掌握直线的一般式方程(重点). 2.理解关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示直线. 3.会进行直线方程的五种形式之间的转化(重、难点). 1、直观想象
2、数学运算
3、数形结合
复习回顾
问题1 :四种表示直线的方程,
点斜式方程 斜截式方程 两点式方程 截距式方程
它们有怎样的区别与联系呢?
区别:应用条件不同,表达形式不同;
( )
联系:
直线上任意点的几何特征
直线的代数表示:直线上的横纵坐标x,y的关系
形
数
追问1:以上四种方程在表示直线时有怎样的局限性
直线的方程 斜率不存在 斜率为0
直线过原点
点斜式
斜截式
两点式
截距式 ( )
y
x
O
x
y
O
x
y
O
探究新知
× √ √
× √ √
× × √
× × ×
探究新知
探究一:直线的方程与二元一次方程的关系
探究二:直线的一般式方程的表达
问题2:能否用一种方程形式表示平面直角坐标系中的任意一条直线
探究新知
直线上任意点
的几何特征
直线的代数表示:直线上任意点的横纵坐标x,y的关系。
关于x,y的
二元一次方程
追问1:在平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程 表示吗?
直线
斜率存在
斜率不存在
(A,B不同时为0)
探究新知
探究新知
追问2:对于任意一个关于,的二元一次方程(A,B不同时为0)是否都表示一条直线?
(A,B不同时为0)
B≠0
B=0
A≠0
知识小结
点斜式、斜截式方程
两点式、截距式方程
(A,B不同时为0)
(A,B不同时为0)
知识小结
直线
平面直角坐标系
问题3: 在方程 中,A,B,C为何值时,方程表示的直线:
探究新知
(A,B不同时为0)
平行于x轴
x
y
O
斜率为0,
在y轴上截距不为0
A=0,B≠0
4.与y轴重合?
2.平行于y轴?
1.平行于x轴?
3.与x轴重合?
A=0
B≠0
C≠0
1.平行于x轴?
问题3: 在方程 中,A,B,C为何值时,方程表示的直线:
探究新知
(A,B不同时为0)
平行于y轴
斜率不存在,
在x轴上截距不为0
A≠0,B=0
4.与y轴重合?
2.平行于y轴?
1.平行于x轴?
3.与x轴重合?
A≠0
B=0
C≠0
2.平行于y轴?
y
x
O
问题3: 在方程 中,A,B,C为何值时,方程表示的直线:
探究新知
(A,B不同时为0)
与x轴重合
x
y
O
斜率为0,
在y轴上截距为0
A=0,B≠0
y=0
4.与y轴重合?
2.平行于y轴?
1.平行于x轴?
3.与x轴重合?
A=0
B≠0
C=0
3.与x轴重合?
问题3: 在方程 中,A,B,C为何值时,方程表示的直线:
探究新知
(A,B不同时为0)
与y轴重合
斜率不存在,
在x轴上截距为0
A≠0,B=0
x=0
4.与y轴重合?
2.平行于y轴?
1.平行于x轴?
3.与x轴重合?
A≠0
B=0
C=0
y
x
O
4.与y轴重合?
直线的方程 斜率不存在 斜率为0
直线过原点
点斜式 × √ √
× √ 斜截式 √
两点式 × × √
截距式 ( ) × × ×
(A,B不同时为0)
y
x
O
x
y
O
x
y
O
知识小结
√ √ √
随堂练习
例1 已知直线经过点A(6,4),斜率为,求直线的点斜式和一般式方程.
随堂练习
例2 把直线的一般式方程化为斜截式,求出直线的斜率以及它在轴与轴上的截距,并画出图形.
课堂总结
平面直角坐标系
直线
二元一次方程
(A,B不同时为0)
随堂练习
1.根据下列条件,写出直线的方程,并把它化为一般式:
(1)经过点,斜率是,
(2)经过点平行于轴;
(3)经过点,;
(4)在轴、 轴的截距分别是,3.
随堂练习
2.求下列直线的斜率以及在y轴上的截距,并画出图形:
(1); (2);
(3)x+2y=0; (4)7x 6y+4=0.
随堂练习
3.已知直线的方程是Ax+By+C=0.
(1)当B≠0时,直线的斜率是多少?当B=0时呢?
(2)系数取什么值时,方程表示经过原点的直线?
习题小结
求直线方程时方程形式的选择技巧
(1)已知一点的坐标,求过该点的直线方程时,通常选用点斜式方程.
(2)已知直线的斜率,通常选用点斜式或斜截式,再由其他条件确定一个定点的坐标或在y轴上的截距.
(3)已知直线在两坐标轴上的截距时,通常选用截距式方程.
(4)已知直线上两点时,通常选用两点式方程.
不管黑猫白猫,抓到老鼠就是好猫!
