第八单元数与形必考题检测卷-数学六年级上册人教版(含答案)
文档属性
| 名称 | 第八单元数与形必考题检测卷-数学六年级上册人教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 17:47:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八单元数与形必考题检测卷-数学六年级上册人教版
一、单选题
1.一列数:0,1,2,3,6,7,14,15,30,____,____,____。这列数是亮亮按照一定规律写下来的,他第一次写“0,1”,第二次写“2,3”,第三次写“6,7”,第四次写“14,15”,就这样接着往下写,这列数的最后三个数应该是下面的( )。
A.31,32,64 B.31,62,63 C.31,32,33 D.31,45,46
2.把一些规格相同的杯子叠起来(如图),4个杯子叠起来高20厘米,6个杯子叠起来高26厘米。n个杯子叠起来的高度可以用下面( )的关系式来表示。
A.6n﹣10 B.3n+11 C.6n﹣4 D.3n+8
3.如图分割下去,第(8)号图形中一共有( )个三角形。
A.24 B.48 C.60 D.无法确定
4.、、、……这一列数中的第10个数应该是( ) 。
A. B. C. D.
5.学校春季运动会上,每个班的所有学生都要参加入场式和团体操。五(1)班入场队列如图:
表演团体操时的几个队列如下,五(1)班的队列是( )
A. B.
C. D.
6.用小棒摆六边形,按这个规律摆4个六边形需要( )根小棒。
A.23 B.22 C.21 D.20
二、判断题
7.1+3+5+7+9+11+13=72。( )
8.已知 表示65, 表示86,那么 表示58。( )
9.3,6,9,12,( ),括号里应该填14。( )
10.用火柴棒按下图所示搭正方形,搭一个正方形用4根火柴棒,搭n个正方形用4n根火柴棒。( )
11.一根木头长10m,要把它平均分成5段,每锯下一段需要8分钟,锯完一共要花40分钟。( )
三、填空题
12.按规律填空。
(1)、、、 。
(2)、、、 。
13. 认真审题,专心填写。
22-12= 32-22= 42-32=
利用你发现的规律直接写出下面算式的结果。
102-92= 1002-992= 2002-1992=
14.用小棒按照如下方式摆图形(每边摆1根小棒):
(1)摆第5个图形需用 根小棒;
(2)摆第n个图形需用 根小棒。
15.用计算器算得:1×8+1=9,12×8+2=98,123×8+3=987,则1234×8+4= 。
16.按如图所示的规律拼图案。
(1)第4个图案中,空白正六边形有 个。
(2)第 个图案中有202个空白正六边形。
17.如图,“杨辉聚六图”是由我国南宋杰出的数学家杨辉所研究出来的,它是由1,2,3,……,35,36无重复排列而成的图形,“杨辉聚六环”其每一环6个数之和均相等,则这个和为 ,其中一环中还差个数,它是 。
四、解决问题
18.仔细观察下面的算式和由“※”组成的图案,完成下列问题:
1+3=4=22
1+3+5=9=31
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算:
1+3+5+7+9+……+19= 。
(2)请猜想:
1+3+5+7+9+……+n= 。(n为奇数)
(3)若有1+3+5+7+9+……+n=625,则n= 。(n为奇数)
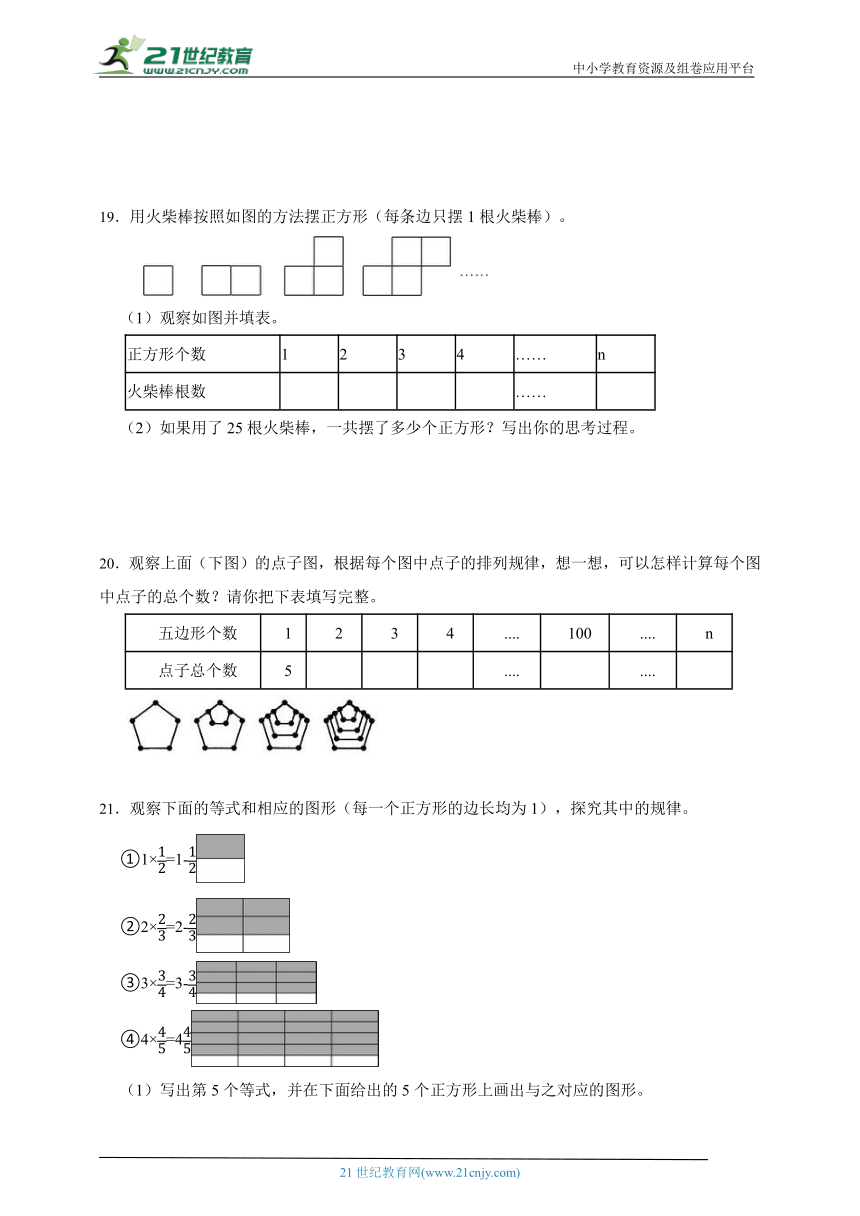
19.用火柴棒按照如图的方法摆正方形(每条边只摆1根火柴棒)。
(1)观察如图并填表。
正方形个数 1 2 3 4 …… n
火柴棒根数 ……
(2)如果用了25根火柴棒,一共摆了多少个正方形?写出你的思考过程。
20.观察上面(下图)的点子图,根据每个图中点子的排列规律,想一想,可以怎样计算每个图中点子的总个数?请你把下表填写完整。
五边形个数 1 2 3 4 .... 100 .... n
点子总个数 5 .... ....
21.观察下面的等式和相应的图形(每一个正方形的边长均为1),探究其中的规律。
①1×=1-
②2×=2-
③3×=3-
④4×=4
(1)写出第5个等式,并在下面给出的5个正方形上画出与之对应的图形。
(2)猜想并写出与第100个图形相对应的等式。
22.用面积是15平方厘米的长方形纸片拼图,第一次用了2个长方形,第二次用更多的长方形把第一次拼出的图全部包围起来,以后每次都把前一次的图包围起来,这样一直拼下去,第5次拼出的图形共有多少平方厘米?第10次拼图共需要多少个这样的长方形?
答案部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】C
7.【答案】(1)正确
8.【答案】(1)错误
9.【答案】(1)错误
10.【答案】(1)错误
11.【答案】(1)错误
12.【答案】(1)
(2)
13.【答案】3;5;7;19;199;399
14.【答案】(1)36
(2)7n+1
15.【答案】9876
16.【答案】(1)18
(2)50
17.【答案】111;26
18.【答案】(1)102
(2)
(3)49
19.【答案】(1)解:
正方形个数 1 2 3 4 …… n
火柴棒根数 4 7 10 13 …… 3n+1
(2)解:设一共摆了n个正方形。
3n+1=25
3n=25﹣1
3n=24
n=24÷3
n=8
答:一共摆了8个正方形。
20.【答案】解:4×2+1
=8+1
=9(个)
4×3+1
=12+1
=13(个)
4×4+1
=16+1
=17(个)
4×100+1
=400+1
=401(个)
4×n+1
=4n+1
=(4n+1)(个)
五边形个数 1 2 3 4 .... 100 .... n
点子总个数 5 9 13 17 .... 401 .... 4n+1
21.【答案】(1)解:5×=5-
(2)解:100×=100-
22.【答案】解:2×5=10(个)
10-1=9(个)
15×(10×9)
=15×90
=1350(平方厘米)
2×10=20(个)
20-1=19(个)
20×19=380(个)
答:第5次拼出的图形共有1350平方厘米,第10次拼图共需要380个这样的长方形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八单元数与形必考题检测卷-数学六年级上册人教版
一、单选题
1.一列数:0,1,2,3,6,7,14,15,30,____,____,____。这列数是亮亮按照一定规律写下来的,他第一次写“0,1”,第二次写“2,3”,第三次写“6,7”,第四次写“14,15”,就这样接着往下写,这列数的最后三个数应该是下面的( )。
A.31,32,64 B.31,62,63 C.31,32,33 D.31,45,46
2.把一些规格相同的杯子叠起来(如图),4个杯子叠起来高20厘米,6个杯子叠起来高26厘米。n个杯子叠起来的高度可以用下面( )的关系式来表示。
A.6n﹣10 B.3n+11 C.6n﹣4 D.3n+8
3.如图分割下去,第(8)号图形中一共有( )个三角形。
A.24 B.48 C.60 D.无法确定
4.、、、……这一列数中的第10个数应该是( ) 。
A. B. C. D.
5.学校春季运动会上,每个班的所有学生都要参加入场式和团体操。五(1)班入场队列如图:
表演团体操时的几个队列如下,五(1)班的队列是( )
A. B.
C. D.
6.用小棒摆六边形,按这个规律摆4个六边形需要( )根小棒。
A.23 B.22 C.21 D.20
二、判断题
7.1+3+5+7+9+11+13=72。( )
8.已知 表示65, 表示86,那么 表示58。( )
9.3,6,9,12,( ),括号里应该填14。( )
10.用火柴棒按下图所示搭正方形,搭一个正方形用4根火柴棒,搭n个正方形用4n根火柴棒。( )
11.一根木头长10m,要把它平均分成5段,每锯下一段需要8分钟,锯完一共要花40分钟。( )
三、填空题
12.按规律填空。
(1)、、、 。
(2)、、、 。
13. 认真审题,专心填写。
22-12= 32-22= 42-32=
利用你发现的规律直接写出下面算式的结果。
102-92= 1002-992= 2002-1992=
14.用小棒按照如下方式摆图形(每边摆1根小棒):
(1)摆第5个图形需用 根小棒;
(2)摆第n个图形需用 根小棒。
15.用计算器算得:1×8+1=9,12×8+2=98,123×8+3=987,则1234×8+4= 。
16.按如图所示的规律拼图案。
(1)第4个图案中,空白正六边形有 个。
(2)第 个图案中有202个空白正六边形。
17.如图,“杨辉聚六图”是由我国南宋杰出的数学家杨辉所研究出来的,它是由1,2,3,……,35,36无重复排列而成的图形,“杨辉聚六环”其每一环6个数之和均相等,则这个和为 ,其中一环中还差个数,它是 。
四、解决问题
18.仔细观察下面的算式和由“※”组成的图案,完成下列问题:
1+3=4=22
1+3+5=9=31
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算:
1+3+5+7+9+……+19= 。
(2)请猜想:
1+3+5+7+9+……+n= 。(n为奇数)
(3)若有1+3+5+7+9+……+n=625,则n= 。(n为奇数)
19.用火柴棒按照如图的方法摆正方形(每条边只摆1根火柴棒)。
(1)观察如图并填表。
正方形个数 1 2 3 4 …… n
火柴棒根数 ……
(2)如果用了25根火柴棒,一共摆了多少个正方形?写出你的思考过程。
20.观察上面(下图)的点子图,根据每个图中点子的排列规律,想一想,可以怎样计算每个图中点子的总个数?请你把下表填写完整。
五边形个数 1 2 3 4 .... 100 .... n
点子总个数 5 .... ....
21.观察下面的等式和相应的图形(每一个正方形的边长均为1),探究其中的规律。
①1×=1-
②2×=2-
③3×=3-
④4×=4
(1)写出第5个等式,并在下面给出的5个正方形上画出与之对应的图形。
(2)猜想并写出与第100个图形相对应的等式。
22.用面积是15平方厘米的长方形纸片拼图,第一次用了2个长方形,第二次用更多的长方形把第一次拼出的图全部包围起来,以后每次都把前一次的图包围起来,这样一直拼下去,第5次拼出的图形共有多少平方厘米?第10次拼图共需要多少个这样的长方形?
答案部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】C
7.【答案】(1)正确
8.【答案】(1)错误
9.【答案】(1)错误
10.【答案】(1)错误
11.【答案】(1)错误
12.【答案】(1)
(2)
13.【答案】3;5;7;19;199;399
14.【答案】(1)36
(2)7n+1
15.【答案】9876
16.【答案】(1)18
(2)50
17.【答案】111;26
18.【答案】(1)102
(2)
(3)49
19.【答案】(1)解:
正方形个数 1 2 3 4 …… n
火柴棒根数 4 7 10 13 …… 3n+1
(2)解:设一共摆了n个正方形。
3n+1=25
3n=25﹣1
3n=24
n=24÷3
n=8
答:一共摆了8个正方形。
20.【答案】解:4×2+1
=8+1
=9(个)
4×3+1
=12+1
=13(个)
4×4+1
=16+1
=17(个)
4×100+1
=400+1
=401(个)
4×n+1
=4n+1
=(4n+1)(个)
五边形个数 1 2 3 4 .... 100 .... n
点子总个数 5 9 13 17 .... 401 .... 4n+1
21.【答案】(1)解:5×=5-
(2)解:100×=100-
22.【答案】解:2×5=10(个)
10-1=9(个)
15×(10×9)
=15×90
=1350(平方厘米)
2×10=20(个)
20-1=19(个)
20×19=380(个)
答:第5次拼出的图形共有1350平方厘米,第10次拼图共需要380个这样的长方形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
