第一单元《长方体和正方体》暑期预习作业(同步练习)-六年级上册数学苏教版(含解析)
文档属性
| 名称 | 第一单元《长方体和正方体》暑期预习作业(同步练习)-六年级上册数学苏教版(含解析) | 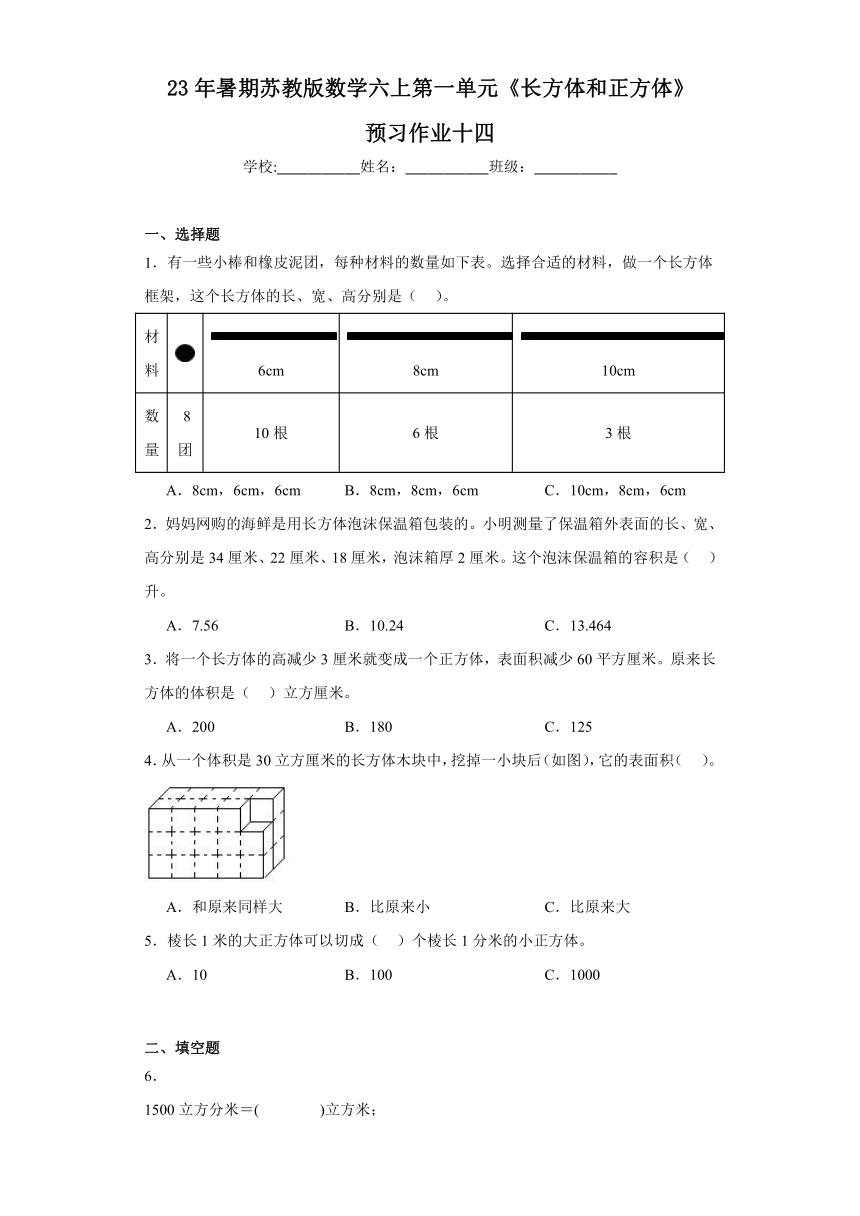 | |
| 格式 | docx | ||
| 文件大小 | 49.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 16:40:47 | ||
图片预览





文档简介
23年暑期苏教版数学六上第一单元《长方体和正方体》
预习作业十四
学校:___________姓名:___________班级:___________
一、选择题
1.有一些小棒和橡皮泥团,每种材料的数量如下表。选择合适的材料,做一个长方体框架,这个长方体的长、宽、高分别是( )。
材料 6cm 8cm 10cm
数量 8团 10根 6根 3根
A.8cm,6cm,6cm B.8cm,8cm,6cm C.10cm,8cm,6cm
2.妈妈网购的海鲜是用长方体泡沫保温箱包装的。小明测量了保温箱外表面的长、宽、高分别是34厘米、22厘米、18厘米,泡沫箱厚2厘米。这个泡沫保温箱的容积是( )升。
A.7.56 B.10.24 C.13.464
3.将一个长方体的高减少3厘米就变成一个正方体,表面积减少60平方厘米。原来长方体的体积是( )立方厘米。
A.200 B.180 C.125
4.从一个体积是30立方厘米的长方体木块中,挖掉一小块后(如图),它的表面积( )。
A.和原来同样大 B.比原来小 C.比原来大
5.棱长1米的大正方体可以切成( )个棱长1分米的小正方体。
A.10 B.100 C.1000
二、填空题
6.
1500立方分米=( )立方米;
一块橡皮的体积大约8( );
时=( )分;
一个饮料瓶大釣能装200( )的果汁。
7.如图是用棱长1厘米的小正方体拼成的图形,它的表面积是( )平方厘米,体积是( )立方厘米。
8.一个正方体底面周长是12分米,它的表面积是( )平方分米,体积是( )立方分米。
9.用1立方厘米的小正方体摆一个棱长6厘米的大正方体,需要小正方体( )个,摆成的正方体的底面积是( )平方厘米。
10.一个长方体的长是14厘米,宽是3厘米,高是2.5厘米,那么它的棱长总和是( )厘米,表面积是( )平方厘米,体积是( )立方厘米。
三、判断题
11.体积是1立方米的正方体木块和长方体木块表面积一定相等。( )
12.把一个大长方体切成4个小长方体,体积不变,表面积变大了。( )
13.下图不可以折成一个正方体。( )
14.一个长方体中(不包括正方体)最多有4个面完全相同。( )
15.一个正方体棱长扩大2倍,它的表面积就扩大4倍,体积就扩大6倍。( )
四、解答题
16.体育馆新建了一个长方体游泳池,长是50米,宽是30米,深是3米。
(1)这个游泳池占地多少平方米?
(2)如果向游泳池内注水,水深2米,那么需要注入多少立方米的水?
17.一个长方体的高减少3分米后,得到一个正方体,表面积比原来减少24平方分米。原来长方体的体积是多少立方分米?
18.建筑工人为体育场修一座游泳池,长60米,宽15米,深1.4米
(1)这个游泳池占地面积多少平方米?
(2)如果在游泳池的底面和四周贴瓷砖,贴瓷砖的面积是多少平方米?
(3)如果往游泳池里放水,使水面到池口的距离是0.2米,需要多少立方米的水?
参考答案:
1.A
【分析】根据长方体的特征:长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,由于长10cm的小棒只有3根,没办法拼成长方体,所以不能用,据此即可选择。
【详解】这个长方体的长是8cm4根,宽和高是6cm8根。
有一些小棒和橡皮泥团,每种材料的数量如下表。选择合适的材料,做一个长方体框架,这个长方体的长、宽、高分别是8cm,6cm,6cm。
故答案为:A
【点睛】本题考查长方体棱长特征以及应用。
2.A
【分析】求出泡沫保温箱的内部长,宽,高是多少厘米,用外面表面的长-2×2,求出内部的长,用外面表面的宽-2×2,求出内部的宽,再用外部的高-2×2,求出内部的高,再根据长方体体积公式:体积=长×宽×高,再根据体积和容积之间的关系,转换单位即可。
【详解】(34-2×2)×(22-2×2)×(18-2×2)
=(34-4)×(22-4)×(18-4)
=30×18×14
=540×14
=7560(立方厘米)
7560立方厘米=7.56升
妈妈网购的海鲜是用长方体泡沫保温箱包装的。小明测量了保温箱外表面的长、宽、高分别是34厘米、22厘米、18厘米,泡沫箱厚2厘米。这个泡沫保温箱的容积是7.56升。
故答案为:A
【点睛】解答本题的关键是求出保温箱内部的长、宽和高的长度;注意单位名数的换算。
3.A
【分析】长方体的高减少3厘米变成一个正方体,说明原来的长方体上下两个底面是正方形,其它四个侧面是形状相同的长方形,减少了去掉的长方体4个侧面的面积,根据减少的表面积求出去掉的长方体一个侧面的面积,并利用长方形的面积公式求出长方体底面的棱长,最后利用“长方体的体积=长×宽×高”求出原来长方体的体积,据此解答。
【详解】
长方体的底面棱长:60÷4÷3
=15÷3
=5(厘米)
长方体的体积:5×5×(5+3)
=5×5×8
=25×8
=200(立方厘米)
所以,原来长方体的体积是200立方厘米。
故答案为:A
【点睛】本题主要考查立体图形的切拼,掌握长方体的特征,根据减少部分的面积求出长方体底面的棱长是解答题目的关键。
4.A
【分析】观察图形可知,从长方体的顶点处挖掉一小块后,表面积比原来减少了3个小正方形的面积,但又增加了3个小正方形的面积,所以表面积不变。据此选择即可。
【详解】由分析可知:
从一个体积是30立方厘米的长方体木块中,挖掉一小块后(如图),它的表面积和原来同样大。
故答案为:A
【点睛】本题考查长方体的表面积,明确表面积的定义是解题的关键。
5.C
【分析】把高级单位转化为低级单位,根据“正方体的体积=棱长×棱长×棱长”分别求出大正方体和小正方体的体积,可以切成小正方体的数量=大正方体的体积÷小正方体的体积,据此解答。
【详解】1米=10分米
(10×10×10)÷(1×1×1)
=1000÷1
=1000(个)
所以,棱长1米的大正方体可以切成1000个棱长1分米的小正方体。
故答案为:C
【点睛】掌握正方体的体积计算公式是解答题目的关键。
6. 1.5 立方厘米/cm3 45 毫升/ml
【分析】根据生活经验,对容积单位、体积单位和数据的大小认识,可知:低级单位立方分米化成高级单位立方米除以进率1000即可;计量一块橡皮的体积用“立方厘米”作单位;高级单位时化成低级单位分乘进率60即可;计量一个饮料瓶的体积用“毫升”作单位。
【详解】1500立方分米=1.5立方米;
一块橡皮的体积大约8立方厘米;
时=45分;
一个饮料瓶大约能装200毫升的果汁。
【点睛】此题考查根据情景选择合适的计量单位以及容积单位、体积单位和时间单位之间的单位换算,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
7. 30 8
【分析】已知小正方体的棱长是1厘米,则一个小正方形的面积是1×1=1(平方厘米),从上面看,可以看到4个小正方形,因此这个立体图形的上下两面的面积之和是4×1×2=8(平方厘米);从左面看,可以看到3个小正方形,因此这个立体图形的左右两面的面积之和是3×1×2=6(平方厘米);从前面看,可以看到8个小正方形,因此这个立体图形的前后两面的面积之和是8×1×2=16(平方厘米);再把这个立体图形的左、右、上、下、前、后的面积相加,即是这个立体图形的表面积。1个正方体的体积是1×1×1=1(立方厘米),一共有8个小正方体,因此这个立体图形的体积是1×8=8(立方厘米)。
【详解】1×1=1(平方厘米)
4×1×2=8(平方厘米)
3×1×2=6(平方厘米)
8×1×2=16(平方厘米)
8+6+16=30(平方厘米)
1×1×1=1(立方厘米)
1×8=8(立方厘米)
它的表面积是30平方厘米,体积是8立方厘米。
【点睛】本题考查了长方体的表面积公式及正方体的体积公式的运用,考查了学生的应变能力及转化能力。
8. 54 27
【分析】根据正方形的周长公式:C=4a,那么a=C÷4,据此求出正方体的棱长,再根据正方体的表面积公式:S=6a2,体积公式:V=a3,把数据代入公式解答。
【详解】12÷4=3(分米)
3×3×6
=9×6
=54(平方分米)
3×3×3
=9×3
=27(立方分米)
它的表面积是54平方分米,体积是27立方分米。
【点睛】此题主要考查正方形的周长公式、正方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
9. 216 36
【分析】1立方厘米的小正方体的棱长为1厘米,摆成一个棱长为6厘米的正方体,那么每个棱长上都有6个小正方体,由此即可求得所需要的小正方体的个数;
摆成的正方体的棱长为6厘米,它的底面是一个边长为6厘米的正方形,根据正方形面积公式:面积=边长×边长;代入数据,即可解答。
【详解】6×6×6
=36×6
=216(个)
6×6=36(平方厘米)
用1立方厘米的小正方体摆一个棱长6厘米的大正方体,需要小正方体216个,摆成的正方体的底面积是36平方厘米。
【点睛】本题考查小正方体拼成大正方体的方法的灵活应用,求得每个大正方体上的小正方体的个数是解决此类问题的关键。
10. 78 169 105
【分析】根据长方体棱长总和公式:棱长总和=(长+宽+高)×4,代入数据,求出长方体棱长总和;
根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,求出长方体表面积;
根据长方体体积公式:体积=长×宽×高,代入数据,求出长方体体积。
【详解】(14+3+2.5)×4
=(17+2.5)×4
=19.5×4
=78(厘米)
(14×3+14×2.5+3×2.5)×2
=(42+35+7.5)×2
=(77+7.5)×2
=84.5×2
=169(平方厘米)
14×3×2.5
=42×2.5
=105(立方厘米)
一个长方体的长是14厘米,宽是3厘米,高是2.5厘米,那么它的棱长总和是78厘米,表面积是169平方厘米,体积是105立方厘米。
【点睛】熟练掌握长方体棱长总和公式,长方体表面积公式和长方体体积公式是解答本题的关键。
11.×
【分析】根据正方体和长方体的体积和表面积的计算公式,设出适当的数据计算即可判断。
【详解】假设正方体边长1分米,长方体的长0.5分米,宽0.5分米,高4分米,则正方体与长方体体积都是1立方分米;
正方体表面积=1×1×6=6(平方分米);
长方体表面积=(0.5×0.5+0.5×4+0.5×4)×2 =8.5(平方分米);
因为6≠8.5;
故答案为:×。
【点睛】本题考查了正方体和长方体的体积与表面积的计算。体积相等的正方体与长方体的表面积不一定相等。
12.√
【分析】根据体积的含义:物体所占空间的大小叫做物体的体积;可知把一个长方体切割成两个小长方体,体积不变;把一个长方体切割成4个小长方体,表面将增加新的面,所以表面积增加;据此解答。
【详解】因为将长方体切成两个长方体后,表面将增加新的面,所以表面积变大了;而把一个长方体分成4个长方体,体积没有变。原说法正确。
故答案为:√。
【点睛】本题主要考查立体图形的切拼,解题时要明确立体图形切割时,体积不变、表面积增大。
13.√
【分析】根据正方体的11种展开图的特征即可解答。
【详解】不属于正方体展开图11种类型中的任意一种,无法折成一个正方体。
故答案为:√。
【点睛】本题主要考查正方体的11种展开图的特征,熟记正方体的11种展开图的特征是解决本题的关键。
14.√
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等;据此解答。
【详解】一般情况,长方体最多有两个面完全相同,最多4条棱长度相等;特殊情况,如果有两个相对的面是正方形时,最多有4个面是完全相同,最多8条棱长度相等。
故答案为:√
【点睛】此题考查的目的是使学生理解掌握长方体的特征。
15.×
【分析】根据正方体的表面积公式:s=6a2,体积公式:v=a3,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积;据此解答即可。
【详解】如果一个正方体的棱长扩大2倍,其表面积就扩大2×2=4倍,体积就扩大2×2×2=8倍,因此原说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握正方体的表面积公式、体积公式,以及因数与积的变化规律的灵活运用。
16.(1)1500平方米
(2)3000立方米
【分析】(1)占地面积,即相当于求底面的面积,底面是一个长方形,根据长方形的面积公式:长×宽,把数代入公式即可求解;
(2)根据长方体的体积公式:长×宽×高,由于水深2米,即高是2米,把数代入公式即可求解。
【详解】(1)50×30=1500(平方米)
答:这个游泳池占地1500平方米。
(2)50×30×2
=1500×2
=3000(立方米)
答:需要注入3000立方米的水。
【点睛】本题主要考查长方形的面积公式以及长方体的体积公式,熟练掌握它们的公式并灵活运用。
17.20立方分米
【分析】因为高去掉3分米后得到一个正方体,所以这个长方体的底面一定是正方形。表面积减少的部分是去掉3分米部分的四个侧面的面积,用表面积减少的部分除以4求出一个侧面的面积,用一个侧面的面积除以3即可求出底面边长,然后求出原来长方体的高,再用底面积乘高求出原来长方体的体积即可。
【详解】24÷4÷3
=6÷3
=2(分米)
2+3=5(分米)
2×2×5
=4×5
=20(立方分米)
答:原来长方体的体积是20立方分米。
【点睛】根据截去后剩下是正方体,可知减少的部分是宽为3分米的4个面,从而可以分别求出长方体的长、宽、高,进而利用长方体体积的计算方法即可求解。
18.(1)900平方米;
(2)1110平方米;
(3)1080立方米
【分析】(1)求游泳池的占地面积,用长×宽计算即可;
(2)将数据代入长方体表面积公式求出长方体下、左右、前后面的面积即可;
(3)由题意可知:水深为1.4-0.2=1.2米,代入长方体的体积公式计算即可。
【详解】(1)60×15=900(平方米)
答:这个游泳池占地面积900平方米。
(2)60×15+60×1.4×2+15×1.4×2
=900+168+42
=1110(平方米)
答:贴瓷砖的面积是1110平方米。
(3)60×15×(1.4-0.2)
=900×1.2
=1080(立方米)
答:需要1080立方米的水。
【点睛】本题考查长方体表面积、体积公式的实际应用,牢记公式是解题的关键。
预习作业十四
学校:___________姓名:___________班级:___________
一、选择题
1.有一些小棒和橡皮泥团,每种材料的数量如下表。选择合适的材料,做一个长方体框架,这个长方体的长、宽、高分别是( )。
材料 6cm 8cm 10cm
数量 8团 10根 6根 3根
A.8cm,6cm,6cm B.8cm,8cm,6cm C.10cm,8cm,6cm
2.妈妈网购的海鲜是用长方体泡沫保温箱包装的。小明测量了保温箱外表面的长、宽、高分别是34厘米、22厘米、18厘米,泡沫箱厚2厘米。这个泡沫保温箱的容积是( )升。
A.7.56 B.10.24 C.13.464
3.将一个长方体的高减少3厘米就变成一个正方体,表面积减少60平方厘米。原来长方体的体积是( )立方厘米。
A.200 B.180 C.125
4.从一个体积是30立方厘米的长方体木块中,挖掉一小块后(如图),它的表面积( )。
A.和原来同样大 B.比原来小 C.比原来大
5.棱长1米的大正方体可以切成( )个棱长1分米的小正方体。
A.10 B.100 C.1000
二、填空题
6.
1500立方分米=( )立方米;
一块橡皮的体积大约8( );
时=( )分;
一个饮料瓶大釣能装200( )的果汁。
7.如图是用棱长1厘米的小正方体拼成的图形,它的表面积是( )平方厘米,体积是( )立方厘米。
8.一个正方体底面周长是12分米,它的表面积是( )平方分米,体积是( )立方分米。
9.用1立方厘米的小正方体摆一个棱长6厘米的大正方体,需要小正方体( )个,摆成的正方体的底面积是( )平方厘米。
10.一个长方体的长是14厘米,宽是3厘米,高是2.5厘米,那么它的棱长总和是( )厘米,表面积是( )平方厘米,体积是( )立方厘米。
三、判断题
11.体积是1立方米的正方体木块和长方体木块表面积一定相等。( )
12.把一个大长方体切成4个小长方体,体积不变,表面积变大了。( )
13.下图不可以折成一个正方体。( )
14.一个长方体中(不包括正方体)最多有4个面完全相同。( )
15.一个正方体棱长扩大2倍,它的表面积就扩大4倍,体积就扩大6倍。( )
四、解答题
16.体育馆新建了一个长方体游泳池,长是50米,宽是30米,深是3米。
(1)这个游泳池占地多少平方米?
(2)如果向游泳池内注水,水深2米,那么需要注入多少立方米的水?
17.一个长方体的高减少3分米后,得到一个正方体,表面积比原来减少24平方分米。原来长方体的体积是多少立方分米?
18.建筑工人为体育场修一座游泳池,长60米,宽15米,深1.4米
(1)这个游泳池占地面积多少平方米?
(2)如果在游泳池的底面和四周贴瓷砖,贴瓷砖的面积是多少平方米?
(3)如果往游泳池里放水,使水面到池口的距离是0.2米,需要多少立方米的水?
参考答案:
1.A
【分析】根据长方体的特征:长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,由于长10cm的小棒只有3根,没办法拼成长方体,所以不能用,据此即可选择。
【详解】这个长方体的长是8cm4根,宽和高是6cm8根。
有一些小棒和橡皮泥团,每种材料的数量如下表。选择合适的材料,做一个长方体框架,这个长方体的长、宽、高分别是8cm,6cm,6cm。
故答案为:A
【点睛】本题考查长方体棱长特征以及应用。
2.A
【分析】求出泡沫保温箱的内部长,宽,高是多少厘米,用外面表面的长-2×2,求出内部的长,用外面表面的宽-2×2,求出内部的宽,再用外部的高-2×2,求出内部的高,再根据长方体体积公式:体积=长×宽×高,再根据体积和容积之间的关系,转换单位即可。
【详解】(34-2×2)×(22-2×2)×(18-2×2)
=(34-4)×(22-4)×(18-4)
=30×18×14
=540×14
=7560(立方厘米)
7560立方厘米=7.56升
妈妈网购的海鲜是用长方体泡沫保温箱包装的。小明测量了保温箱外表面的长、宽、高分别是34厘米、22厘米、18厘米,泡沫箱厚2厘米。这个泡沫保温箱的容积是7.56升。
故答案为:A
【点睛】解答本题的关键是求出保温箱内部的长、宽和高的长度;注意单位名数的换算。
3.A
【分析】长方体的高减少3厘米变成一个正方体,说明原来的长方体上下两个底面是正方形,其它四个侧面是形状相同的长方形,减少了去掉的长方体4个侧面的面积,根据减少的表面积求出去掉的长方体一个侧面的面积,并利用长方形的面积公式求出长方体底面的棱长,最后利用“长方体的体积=长×宽×高”求出原来长方体的体积,据此解答。
【详解】
长方体的底面棱长:60÷4÷3
=15÷3
=5(厘米)
长方体的体积:5×5×(5+3)
=5×5×8
=25×8
=200(立方厘米)
所以,原来长方体的体积是200立方厘米。
故答案为:A
【点睛】本题主要考查立体图形的切拼,掌握长方体的特征,根据减少部分的面积求出长方体底面的棱长是解答题目的关键。
4.A
【分析】观察图形可知,从长方体的顶点处挖掉一小块后,表面积比原来减少了3个小正方形的面积,但又增加了3个小正方形的面积,所以表面积不变。据此选择即可。
【详解】由分析可知:
从一个体积是30立方厘米的长方体木块中,挖掉一小块后(如图),它的表面积和原来同样大。
故答案为:A
【点睛】本题考查长方体的表面积,明确表面积的定义是解题的关键。
5.C
【分析】把高级单位转化为低级单位,根据“正方体的体积=棱长×棱长×棱长”分别求出大正方体和小正方体的体积,可以切成小正方体的数量=大正方体的体积÷小正方体的体积,据此解答。
【详解】1米=10分米
(10×10×10)÷(1×1×1)
=1000÷1
=1000(个)
所以,棱长1米的大正方体可以切成1000个棱长1分米的小正方体。
故答案为:C
【点睛】掌握正方体的体积计算公式是解答题目的关键。
6. 1.5 立方厘米/cm3 45 毫升/ml
【分析】根据生活经验,对容积单位、体积单位和数据的大小认识,可知:低级单位立方分米化成高级单位立方米除以进率1000即可;计量一块橡皮的体积用“立方厘米”作单位;高级单位时化成低级单位分乘进率60即可;计量一个饮料瓶的体积用“毫升”作单位。
【详解】1500立方分米=1.5立方米;
一块橡皮的体积大约8立方厘米;
时=45分;
一个饮料瓶大约能装200毫升的果汁。
【点睛】此题考查根据情景选择合适的计量单位以及容积单位、体积单位和时间单位之间的单位换算,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
7. 30 8
【分析】已知小正方体的棱长是1厘米,则一个小正方形的面积是1×1=1(平方厘米),从上面看,可以看到4个小正方形,因此这个立体图形的上下两面的面积之和是4×1×2=8(平方厘米);从左面看,可以看到3个小正方形,因此这个立体图形的左右两面的面积之和是3×1×2=6(平方厘米);从前面看,可以看到8个小正方形,因此这个立体图形的前后两面的面积之和是8×1×2=16(平方厘米);再把这个立体图形的左、右、上、下、前、后的面积相加,即是这个立体图形的表面积。1个正方体的体积是1×1×1=1(立方厘米),一共有8个小正方体,因此这个立体图形的体积是1×8=8(立方厘米)。
【详解】1×1=1(平方厘米)
4×1×2=8(平方厘米)
3×1×2=6(平方厘米)
8×1×2=16(平方厘米)
8+6+16=30(平方厘米)
1×1×1=1(立方厘米)
1×8=8(立方厘米)
它的表面积是30平方厘米,体积是8立方厘米。
【点睛】本题考查了长方体的表面积公式及正方体的体积公式的运用,考查了学生的应变能力及转化能力。
8. 54 27
【分析】根据正方形的周长公式:C=4a,那么a=C÷4,据此求出正方体的棱长,再根据正方体的表面积公式:S=6a2,体积公式:V=a3,把数据代入公式解答。
【详解】12÷4=3(分米)
3×3×6
=9×6
=54(平方分米)
3×3×3
=9×3
=27(立方分米)
它的表面积是54平方分米,体积是27立方分米。
【点睛】此题主要考查正方形的周长公式、正方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
9. 216 36
【分析】1立方厘米的小正方体的棱长为1厘米,摆成一个棱长为6厘米的正方体,那么每个棱长上都有6个小正方体,由此即可求得所需要的小正方体的个数;
摆成的正方体的棱长为6厘米,它的底面是一个边长为6厘米的正方形,根据正方形面积公式:面积=边长×边长;代入数据,即可解答。
【详解】6×6×6
=36×6
=216(个)
6×6=36(平方厘米)
用1立方厘米的小正方体摆一个棱长6厘米的大正方体,需要小正方体216个,摆成的正方体的底面积是36平方厘米。
【点睛】本题考查小正方体拼成大正方体的方法的灵活应用,求得每个大正方体上的小正方体的个数是解决此类问题的关键。
10. 78 169 105
【分析】根据长方体棱长总和公式:棱长总和=(长+宽+高)×4,代入数据,求出长方体棱长总和;
根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,求出长方体表面积;
根据长方体体积公式:体积=长×宽×高,代入数据,求出长方体体积。
【详解】(14+3+2.5)×4
=(17+2.5)×4
=19.5×4
=78(厘米)
(14×3+14×2.5+3×2.5)×2
=(42+35+7.5)×2
=(77+7.5)×2
=84.5×2
=169(平方厘米)
14×3×2.5
=42×2.5
=105(立方厘米)
一个长方体的长是14厘米,宽是3厘米,高是2.5厘米,那么它的棱长总和是78厘米,表面积是169平方厘米,体积是105立方厘米。
【点睛】熟练掌握长方体棱长总和公式,长方体表面积公式和长方体体积公式是解答本题的关键。
11.×
【分析】根据正方体和长方体的体积和表面积的计算公式,设出适当的数据计算即可判断。
【详解】假设正方体边长1分米,长方体的长0.5分米,宽0.5分米,高4分米,则正方体与长方体体积都是1立方分米;
正方体表面积=1×1×6=6(平方分米);
长方体表面积=(0.5×0.5+0.5×4+0.5×4)×2 =8.5(平方分米);
因为6≠8.5;
故答案为:×。
【点睛】本题考查了正方体和长方体的体积与表面积的计算。体积相等的正方体与长方体的表面积不一定相等。
12.√
【分析】根据体积的含义:物体所占空间的大小叫做物体的体积;可知把一个长方体切割成两个小长方体,体积不变;把一个长方体切割成4个小长方体,表面将增加新的面,所以表面积增加;据此解答。
【详解】因为将长方体切成两个长方体后,表面将增加新的面,所以表面积变大了;而把一个长方体分成4个长方体,体积没有变。原说法正确。
故答案为:√。
【点睛】本题主要考查立体图形的切拼,解题时要明确立体图形切割时,体积不变、表面积增大。
13.√
【分析】根据正方体的11种展开图的特征即可解答。
【详解】不属于正方体展开图11种类型中的任意一种,无法折成一个正方体。
故答案为:√。
【点睛】本题主要考查正方体的11种展开图的特征,熟记正方体的11种展开图的特征是解决本题的关键。
14.√
【分析】根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等;据此解答。
【详解】一般情况,长方体最多有两个面完全相同,最多4条棱长度相等;特殊情况,如果有两个相对的面是正方形时,最多有4个面是完全相同,最多8条棱长度相等。
故答案为:√
【点睛】此题考查的目的是使学生理解掌握长方体的特征。
15.×
【分析】根据正方体的表面积公式:s=6a2,体积公式:v=a3,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积;据此解答即可。
【详解】如果一个正方体的棱长扩大2倍,其表面积就扩大2×2=4倍,体积就扩大2×2×2=8倍,因此原说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握正方体的表面积公式、体积公式,以及因数与积的变化规律的灵活运用。
16.(1)1500平方米
(2)3000立方米
【分析】(1)占地面积,即相当于求底面的面积,底面是一个长方形,根据长方形的面积公式:长×宽,把数代入公式即可求解;
(2)根据长方体的体积公式:长×宽×高,由于水深2米,即高是2米,把数代入公式即可求解。
【详解】(1)50×30=1500(平方米)
答:这个游泳池占地1500平方米。
(2)50×30×2
=1500×2
=3000(立方米)
答:需要注入3000立方米的水。
【点睛】本题主要考查长方形的面积公式以及长方体的体积公式,熟练掌握它们的公式并灵活运用。
17.20立方分米
【分析】因为高去掉3分米后得到一个正方体,所以这个长方体的底面一定是正方形。表面积减少的部分是去掉3分米部分的四个侧面的面积,用表面积减少的部分除以4求出一个侧面的面积,用一个侧面的面积除以3即可求出底面边长,然后求出原来长方体的高,再用底面积乘高求出原来长方体的体积即可。
【详解】24÷4÷3
=6÷3
=2(分米)
2+3=5(分米)
2×2×5
=4×5
=20(立方分米)
答:原来长方体的体积是20立方分米。
【点睛】根据截去后剩下是正方体,可知减少的部分是宽为3分米的4个面,从而可以分别求出长方体的长、宽、高,进而利用长方体体积的计算方法即可求解。
18.(1)900平方米;
(2)1110平方米;
(3)1080立方米
【分析】(1)求游泳池的占地面积,用长×宽计算即可;
(2)将数据代入长方体表面积公式求出长方体下、左右、前后面的面积即可;
(3)由题意可知:水深为1.4-0.2=1.2米,代入长方体的体积公式计算即可。
【详解】(1)60×15=900(平方米)
答:这个游泳池占地面积900平方米。
(2)60×15+60×1.4×2+15×1.4×2
=900+168+42
=1110(平方米)
答:贴瓷砖的面积是1110平方米。
(3)60×15×(1.4-0.2)
=900×1.2
=1080(立方米)
答:需要1080立方米的水。
【点睛】本题考查长方体表面积、体积公式的实际应用,牢记公式是解题的关键。
