沪科版八年级上册数学期中考试试卷(含解析)
文档属性
| 名称 | 沪科版八年级上册数学期中考试试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
沪科版八年级上册数学期中考试试题
一、选择题:本大题共10小题,每小题3分,共30分。
1.下列函数中,是一次函数的有( )
A. B. C. D.(为常数)
2.下列命题中是假命题的是( )
A.一个锐角的补角大于这个角
B.凡能被2整除的数,末位数字必是偶数
C.两条直线被第三条直线所截,同旁内角互补
D.相反数等于它本身的数是0
3.已知到轴距离为2,到轴距离为1,且在第四象限,则点的坐标为( )
A. B. C. D.
4.点,是函数图像上两点,则与的大小关系( )
A. B. C. D.无法确定
5.线段是由线段平移得到的,点对应点为,则点的对应点的坐标为( )
A. B. C. D.
6.一个等腰三角形的两边长分别是2和5,则这个三角形的周长为( )
A.5 B.9 C.12 D.9或12
7.已知一次函数与图象在轴上相交于同一点,则的值是( )
A.4 B. C. D.
8.对于平面直角坐标系中的点,若点的坐标为(其中为常数,且),则称点为点的“属派生点”,例如,的“2属派生点”为,即,若点的“3属派生点”的坐标为,下列选项中符合条件的点的坐标为
A. B. C. D.
9.下列各图中不能表示是的函数的是( )
A.B.C. D.
10.如图,且平行于轴,下列说法正确的是( )
A.和关于轴对称 B.和关于轴对称
C.和的纵坐标相同 D.和的横坐标相同
二、填空题:本大题共9小题,每小题3分,共18分。
11.函数中,自变量x的取值范围是_____.
12.已知一次函数,则________.
13.在中,,过点作于点,,则________.
14.如图,有一种动画程序,屏幕上正方形是黑色区域(含正方形边界),其中,,,,用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能使黑色区域变白的取值范围是____________.
15.函数有意义,则自变量x的取值范围是___.
16.如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,则∠ACD的度数为________.
三、解答题:本大题共10小题,共72分。
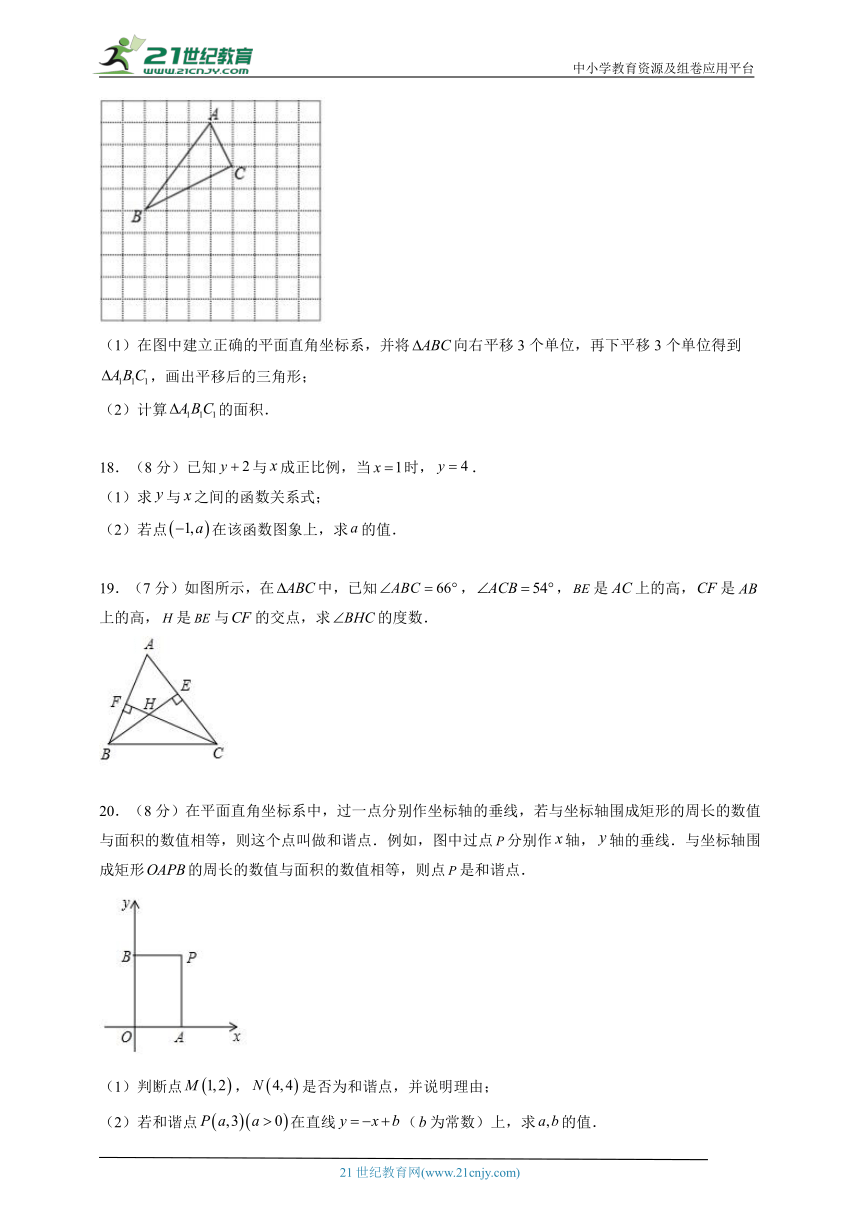
17.(6分)如图,在正方形网格中,若,按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系,并将向右平移3个单位,再下平移3个单位得到,画出平移后的三角形;
(2)计算的面积.
18.(8分)已知与成正比例,当时,.
(1)求与之间的函数关系式;
(2)若点在该函数图象上,求的值.
19.(7分)如图所示,在中,已知,,是上的高,是上的高,是与的交点,求的度数.
20.(8分)在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如,图中过点分别作轴,轴的垂线.与坐标轴围成矩形的周长的数值与面积的数值相等,则点是和谐点.
(1)判断点,是否为和谐点,并说明理由;
(2)若和谐点在直线(为常数)上,求的值.
21.(8分)端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程,与时间之间的函数关系的图象请根据图象提供的信息,解决下列问题:
图中E点的坐标是______,题中______,甲在途中休息______h;
求线段CD的解析式,并写出自变量x的取值范围;
两人第二次相遇后,又经过多长时间两人相距20km?
22.(9分)如图,在中,平分交于点,延长至点平分,且的延长线交于点,若.
求证:;
求的度数;
若在图中继续作与的平分线交于点,作与的平分线交于点,作与的平分线交于点,以此类推,作与的平分线交于点,请用含有的式了表示的度数(直接写答案).
23.(8分)今年某市水果大丰收,两个水果基地分别收获同种水果件、件,现需把这些水果全部运往甲、乙两销售点,从基地运往甲、乙两销售点的费用分别为每件元和元,从基地运往甲、乙两销售点的费用分别为每件元和元,现甲销售点需要水果件,乙销售点需要水果件.
设从基地运往甲销售点水果件,总运费为元,请用含的代数式表示,并写出的取值范围;
若总运费不超过元,且基地运往甲销售点的水果不低于件,试确定运费最低的运输方案,并求出最低运费.
24.(9分)如图,的三边长分别为.
求的取值范围;
当的周长为偶数时,求;
若为等腰三角形,求.
25.(9分)已知一次函数,
若函数图象平行于直线,求的值;
若函数值随自变量的增大而减小,求的取值范围:
若函数图象不经过第二象限,求的取值范围.
参考答案
1.B
【分析】
根据一次函数的定义进行选择即可.
【详解】
A.未知数的指数是2,故不符合题意;
B.只含有一个未知数,且未知数的指数是1的等式是一次函数,故符合题意;
C.未知数在分母的位置,故不符合题意;
D.当时,不符合题意;
故答案选B.
【点睛】
本题考查的是一次函数的定义与识别,能够根据定义准确判断出一次函数是解题的关键.
2.C
【解析】
试题分析:利用锐角的性质、偶数的定义、平行线的性质及相反数的定义分别判断后即可确定正确的选项.
A、一个锐角的补角大于这个角,正确,是真命题,不符合题意;
B、凡能被2整除的数,末尾数字必是偶数,正确,是真命题,不符合题意;
C、两条平行直线被第三条直线所截,同旁内角才互补,故错误,是假命题,符合题意;
D、相反数等于他本身的数是0,正确,是真命题,不符合题意
考点:命题与定理.
3.B
【分析】
平面内一点到x轴的距离为该点纵坐标的绝对值,到y轴的距离为该点横坐标的绝对值,因为点M在第四象限,根据第四象限点坐标的特征即可选出答案.
【详解】
设点M的坐标为
∵点到轴距离为2,到轴距离为1
∴
∵点M在第四象限,
∴
∴,
∴点M坐标为(1,-2)
故选B.
【点睛】
本题考查的是平面直角坐标系中点的坐标特征,能够根据第四象限内点的坐标特征确定点M的坐标是解题的关键.
4.A
【分析】
根据一次函数的增减性进行解答即可.
【详解】
∵函数中
∴函数的增减性是y随x的增大而减小
又∵-2<3
∴
故答案选A.
【点睛】
本题考查的是一次函数的性质,能够根据解析式判断出一次函数的增减性是解题的关键.
5.D
【分析】
先根据点A和它的对应点C的坐标之间的变化规律得到图形的变换规律,然后利用此规律写出点B的对应点D的坐标即可.
【详解】
∵点对应点为
∴线段CD是由线段AB先向右平移3-(-1)=4个单位,向上平移5-2=3个单位。
∵点是点的对应点
∴点D的横坐标为-2+4=2,纵坐标为-1+3=2
∴点D的坐标为(2,2)
故答案选D.
【点睛】
本题考查的是图形的平移的特征,能够根据点A与点C的坐标总结出图形的平移规律是解题的关键.
6.C
【分析】
根据等腰三角形的特征和三角形三边之间的关系分2是腰与5是腰两种情况去讨论,即可选出答案.
【详解】
当2是腰,5是底时,三边长分别是2,2,5,因为2+2<5,所以这种情况不能组成三角形;
当5是腰,2是底时,三边长分别是5,5,2,因为2+5>5,符合三角形三边关系,此时三角形的周长为2+5+5=12.
故答案选C.
【点睛】
本题考查的是等腰三角形的性质和三角形三边关系,能够分情况讨论是解题的关键.
7.B
【分析】
根据“一次函数与图象在轴上相交于同一点”,可知两个图像与x轴的交点是同一个点,用a,b分别表示出这个交点的横坐标,然后联立即可.
【详解】
在中,令,得;
在中,令,得
∵一次函数与图象在轴上相交于同一点
∴
∴
故选B.
【点睛】
本题考查的是一次函数同解问题,能够根据图像交点相同想到用同解联立来解答是解题的关键.
8.C
【分析】
根据题干新定义的概念,理解点P的“k属派生点”的概念,设点P的坐标为(a,b),可得,进而选择即可.
【详解】
设点P的坐标为,因为点P的“k属派生点”的坐标满足,
所以
A.3×1+2=5≠12,不符合题意;
B.2×3+1=7≠12,不符合题意;
C.2×3+6=12,符合题意;
D.6×3+2=20≠12不符合题意;
综上答案选C.
【点睛】
本题考查的新定义概念,能够读懂题意是解题的关键.
9.D
【分析】
主要考查了函数的定义.注意函数的意义反映在图象上简单的判断方法是:作垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.
【详解】
A、B、C作垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点,能表示y是x的函数,故不符合题意;
D. 作垂直x轴的直线在左右平移的过程中与函数图象存在2个交点,不能表示y是x的函数,故D符合题意;
故选:D.
【点睛】
此题考查函数的概念,解题关键在于熟悉掌握函数的定义.
10.C
【分析】
根据与x轴平行的直线上点的坐标特征解析判断.
【详解】
∵AD∥BC∥x轴,
∴点A与点D的纵坐标相同,点B与点C的纵坐标相同
故选C.
【点睛】
此题考查坐标与图形性质,解题关键在于熟练分析坐标特征及判断.
11..
【详解】
∵在实数范围内有意义,
∴
∴
故答案为
12.-1
【分析】
根据一次函数的定义可知未知数的指数应该是1,且一次项系数不能为0,据此列式计算即可.
【详解】
根据题意可知,解得,所以,故答案为-1.
【点睛】
本题考查的是一次函数的定义,熟知一次函数的定义是解题的关键.
13.82°
【分析】
根据三角形的内角和是180°进行求解即可.
【详解】
如图,∵AD⊥BC,
∴∠ADC=90°,
又∵∠CAD=22°,
∴∠C=180°-90°-22°=68°,
∴∠BAC=180°-∠B-∠C=180°-30°-68°=82°
故答案为82°.
【点睛】
本题考查的是三角形的内角和定理,能够利用三角形的内角和定理进行解题是关键.
14.
【分析】
根据直线解析式可知直线必过一三象限,当经过点B时b的值最小,当经过点D是b的值最大,由此得出结论即可.
【详解】
∵直线中
∴此直线必过一三象限
∵,
当直线经过点B时,-2+b=-2,解得b=0;
当直线经过点D时,-4+b=-1,解得b=3;
∴
故答案为.
【点睛】
本题考查的是一次函数的实际应用,能够根据题意将问题转换成一次函数问题是解题的关键.
15.且
【分析】
求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件进行求解即可.
【详解】
要使在实数范围内有意义,
必须
所以x≥1且,
故答案为:x≥1且.
【点睛】
本题考查了函数自变量的取值范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.
16.83°
【分析】
由DF⊥AB,在Rt△BDF中可求得∠B;再由∠ACD=∠A+∠B可求得∠ACD的度数.
【详解】
解:∵DF⊥AB,
∴∠B+∠D=90°,
∴∠B=90°-∠D=90°-42°=48°,
∴∠ACD=∠A+∠B=35°+48°=83°.
故答案为83°
【点睛】
本题主要考查了三角形内角和定理以及三角形外角性质的综合应用,解题时注意:三角形内角和是180°,三角形的一个外角等于和它不相邻的两个内角的和.
17.(1)见解析;(2)4
【分析】
(1)根据点A坐标建立坐标系即可,根据平移先找出对应点,然后即可画出图形;
(2)利用割补法即可求面积.
【详解】
解:因为点A(0,3),所以点A在y轴上,据此建立直角坐标系即可,如下图,从而可知点B坐标为(-3,-1),点C坐标为(1,1),根据平移可知A、B、C对应点坐标分别为(3,0)、(-4,0)、(4,-2),描点连线;
(2),故的面积是4.
【点睛】
本题考查的是直角坐标系,平移的性质和三角形面积的求法,能够充分调动所学知识是解题的关键.
18.(1);(2)
【分析】
(1)根据“与成正比例”,设,将,代入求解即可;
(2)将点坐标代入(1)中解析式即可.
【详解】
解:(1)∵与成正比例
∴设
将,代入得,即
∴,即
∴与之间的函数关系式为;
(2)∵点在该函数图象上
将其代入到中有,解得
∴的值是-8.
【点睛】
本题考查的是一次函数问题,能够根据题意列出一次函数式是解题的关键.
19.120°
【分析】
根据∠ABC=66°,∠ACB=54°,先求∠A得度数,再求∠ABE与∠ACF的度数,最后利用三角形的外角定理即可求得答案.
【详解】
解:∵∠ABC=66°,∠ACB=54°
∴∠A=180°-∠ABC-∠ACB=180°-66°-54°=60°
又∵BE是AC边上的高
∴∠AEB=∠BEC=90°
∴∠ABE=180°-∠A-∠AEB=180°-60°-90°=30°
同理∠ACF=30°
∴∠BHC=∠BEC+∠ACF=90°+30°=120°
【点睛】
本题考查了三角形内角和定理和三角形外角定理,能够根据这些知识解答问题是关键.
20.(1)点M不是和谐点,点N是和谐点;(2)的值分别是6,9
【分析】
(1)根据和谐点的定义。利用矩形的面积和周长公式进行证明即可;
(2)利用和谐点的定义列出关于a的方程,由此求a,然后将点P的坐标代入直线方程求解b值即可.
【详解】
解:(1)∵
∴点M不是和谐点,点N是和谐点;
(2)∵点P是和谐点
∴,解得
∴点P的坐标为
∵点P在直线上
∴代入得
解得
∴的值分别是6,9.
【点睛】
本题考查的是新定义和列式计算的能力,能够读懂题意是解题的关键.
21.,100,1;直线CD的解析式为:;两人第二次相遇后,又经过时或时两人相距
【分析】
(1)根据速度和时间列方程:60×1+m=160,可得m=100,根据D的坐标可计算直线OD的解析式,从图中知E的横坐标为2,可得E的坐标,根据点E到D的时间差及速度可得休息的时间;
(2)利用待定系数法求直线CD的解析式;
(3)先计算第二次相遇的时间:y=360时代入y=80x可得x的值,再计算x=5时直线OD的路程,可得路程差为40km,所以存在两种情况:两人相距20km,列方程可得结论.
【详解】
由图形得,
设OD的解析式为:,
把代入得:,,
:,
当时,,
,
由题意得:,,
,
故答案为,100,1;
,,
直线AE:,
当时,,
,
,
,
设CD的解析式为:,
把,代入得:,解得:,
直线CD的解析式为:;
的解析式为:,
当时,,
,
出发5h时两个相距40km,
把代入得:,
出发时两人第二次相遇,
当时,,
,,
当时,,
,,
答:两人第二次相遇后,又经过时或时两人相距
【点睛】
本题考查了一次函数的应用,读懂函数图象,理解横、纵坐标表示的含义,熟练掌握一次函数的相关知识、利用数形结合思想是解题的关键.
22.(1)证明见解析;(2)∠E=10°;(3)∠En+l=∠E.
【分析】
(1)根据三角形的一个外角等于和它不相邻的两个内角的和,得出∠DCE=∠A+∠D,∠DFE=∠DCE+∠E,将第一式代入第二式即可得证;
(2)根据角平分线及三角形外角的性质得出∠ECG=∠DCG=(∠D+∠DBC),∠ECG=∠E+∠EBC=∠E+
∠DBC,则∠D=2∠E,再利用上题结论∠DFE=∠A+∠D+∠E,将已知条件代入,即可求出∠E的度数;
(3)先根据角平分线及三角形外角的性质得出∠E1=∠E,同理得出∠E2=∠E1,则∠E2=∠E=∠E,由此得出规律∠En+l=∠E.
【详解】
(1)证明:∵∠DCE=∠A+∠D,∠DFE=∠DCE+∠E,
∴∠DFE=∠A+∠D+∠E;
(2)解:∵∠DCG=∠D+∠DBC,CE平分∠DCG,
∴∠ECG=∠DCG=(∠D+∠DBC),
∵BE平分∠DBC,
∴∠EBC=∠DBC,
∵∠ECG=∠E+∠EBC=∠E+∠DBC,
∴∠E+∠DBC=(∠D+∠DBC),
∴∠E=∠D,
∴∠D=2∠E.
∵∠DFE=63°,∠A=33°,∠DFE=∠A+∠D+∠E,
∴∠D+∠E=∠DEF-∠A=63°-33°=30°,
∴2∠E+∠E=30°,
∴∠E=10°;
(3)∵∠ECG=∠E+∠EBC,CE1平分∠ECG,
∴∠E1CG=∠ECG=(∠E+∠EBC).
∵BE1平分∠EBC,
∴∠E1BC=∠EBC.
∵∠E1CG=∠E1+∠E1BC=∠E1+∠EBC,
∴∠E1+∠EBC=(∠E+∠EBC),
∴∠E1=∠E.
同理:∠E2=∠E1,
∴∠E2=∠E=∠E,
∴∠En+l=∠E.
【点睛】
此题考查三角形的角平分线,三角形的外角的性质,(3)中得出∠E1=∠E,是解题的关键.
23.(1)W=35x+11200(80≤x≤380);(2)18200元,从A基地运往甲销售点的水果200件,运往乙销售点的水果180件;从B基地运往甲销售点的水果200件,运往乙销售点的水果120件.
【分析】
(1)表示出从A基地运往乙销售点的水果件数,从B基地运往甲、乙两个销售点的水果件数,然后根据运费=单价×数量列式整理即可得解,再根据运输水果的数量不小于0列出不等式求解得到x的取值范围;
(2)根据一次函数的增减性确定出运费最低时的运输方案,然后求解即可.
【详解】
(1)设从A基地运往甲销售点水果x件,则从A基地运往乙销售点的水果(380-x)件,
从B基地运往甲销售点水果(400-x)件,运往乙基地(x-80)件,
由题意得,W=40x+20(380-x)+15(400-x)+30(x-80),
=35x+11200,
即W=35x+11200,
∵ ,
∴80≤x≤380,
即x的取值范围是80≤x≤380;
(2)∵A地运往甲销售点的水果不低于200件,
∴x≥200,
∵k=35>0,
∴运费W随着x的增大而增大,
∴当x=200时,运费最低,为35×200+11200=18200元<18300元,
此时,方案为:
从A基地运往甲销售点的水果200件,运往乙销售点的水果180件,
从B基地运往甲销售点的水果200件,运往乙销售点的水果120件.
【点睛】
此题考查一次函数的应用,一元一次不等式组的应用,读懂题目信息,准确表示出从A、B两个基地运往甲、乙两个销售点的水果的件数是解题的关键.
24.(1)4<x<14;(2)x=6、8、10,12;(3)x=5或9.
【分析】
(1)根据三角形的第三边大于两边之差,而小于两边之和进行计算;
(2)要使周长是偶数,因为其它两边之和是13,则x应是奇数;
(3)根据等腰三角形的定义:有两边相等的三角形是等腰三角形,则x=4或9,再根据(1)中的取值范围进行取舍.
【详解】
△ABC的三边长分别为5、9、x,
(1)根据三角形的第三边大于两边之差,而小于两边之和,得9-5<x<9+5,即4<x<14;
(2)因为已知的两边之和是14,为偶数,要使周长为偶数,则第三边应是偶数,即x=6、8、10,12;
(3)若△ABC为等腰三角形,x=5或9.
【点睛】
此题考查三角形的三边关系,理解数的奇偶性,理解等腰三角形的性质,解题关键在于注意一定要检查是否符合三角形的三边关系.
25.(1)m=-1;(2)m<-;(3)-<m≤1.
【分析】
(1)根据两直线平行的性质求出m的值;
(2)根据一次函数的性质列出关于m的不等式求出m的取值范围即可;
(3)根据一次函数的性质列出关于m的不等式组求出m的取值范围即可.
【详解】
(1)∵函数图象平行于直线y=x+1,
∴2m+3=1,解得m=-1;
(2)∵该函数的值y随自变量x的增大而减小,
∴2m+3<0,解得m<-;
(3)∵该函数图象不经过第二象限,
∴ ,解得-<m≤1.
【点睛】
此题考查一次函数的性质,熟知一次函数的图象与系数的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版八年级上册数学期中考试试题
一、选择题:本大题共10小题,每小题3分,共30分。
1.下列函数中,是一次函数的有( )
A. B. C. D.(为常数)
2.下列命题中是假命题的是( )
A.一个锐角的补角大于这个角
B.凡能被2整除的数,末位数字必是偶数
C.两条直线被第三条直线所截,同旁内角互补
D.相反数等于它本身的数是0
3.已知到轴距离为2,到轴距离为1,且在第四象限,则点的坐标为( )
A. B. C. D.
4.点,是函数图像上两点,则与的大小关系( )
A. B. C. D.无法确定
5.线段是由线段平移得到的,点对应点为,则点的对应点的坐标为( )
A. B. C. D.
6.一个等腰三角形的两边长分别是2和5,则这个三角形的周长为( )
A.5 B.9 C.12 D.9或12
7.已知一次函数与图象在轴上相交于同一点,则的值是( )
A.4 B. C. D.
8.对于平面直角坐标系中的点,若点的坐标为(其中为常数,且),则称点为点的“属派生点”,例如,的“2属派生点”为,即,若点的“3属派生点”的坐标为,下列选项中符合条件的点的坐标为
A. B. C. D.
9.下列各图中不能表示是的函数的是( )
A.B.C. D.
10.如图,且平行于轴,下列说法正确的是( )
A.和关于轴对称 B.和关于轴对称
C.和的纵坐标相同 D.和的横坐标相同
二、填空题:本大题共9小题,每小题3分,共18分。
11.函数中,自变量x的取值范围是_____.
12.已知一次函数,则________.
13.在中,,过点作于点,,则________.
14.如图,有一种动画程序,屏幕上正方形是黑色区域(含正方形边界),其中,,,,用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能使黑色区域变白的取值范围是____________.
15.函数有意义,则自变量x的取值范围是___.
16.如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,则∠ACD的度数为________.
三、解答题:本大题共10小题,共72分。
17.(6分)如图,在正方形网格中,若,按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系,并将向右平移3个单位,再下平移3个单位得到,画出平移后的三角形;
(2)计算的面积.
18.(8分)已知与成正比例,当时,.
(1)求与之间的函数关系式;
(2)若点在该函数图象上,求的值.
19.(7分)如图所示,在中,已知,,是上的高,是上的高,是与的交点,求的度数.
20.(8分)在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如,图中过点分别作轴,轴的垂线.与坐标轴围成矩形的周长的数值与面积的数值相等,则点是和谐点.
(1)判断点,是否为和谐点,并说明理由;
(2)若和谐点在直线(为常数)上,求的值.
21.(8分)端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程,与时间之间的函数关系的图象请根据图象提供的信息,解决下列问题:
图中E点的坐标是______,题中______,甲在途中休息______h;
求线段CD的解析式,并写出自变量x的取值范围;
两人第二次相遇后,又经过多长时间两人相距20km?
22.(9分)如图,在中,平分交于点,延长至点平分,且的延长线交于点,若.
求证:;
求的度数;
若在图中继续作与的平分线交于点,作与的平分线交于点,作与的平分线交于点,以此类推,作与的平分线交于点,请用含有的式了表示的度数(直接写答案).
23.(8分)今年某市水果大丰收,两个水果基地分别收获同种水果件、件,现需把这些水果全部运往甲、乙两销售点,从基地运往甲、乙两销售点的费用分别为每件元和元,从基地运往甲、乙两销售点的费用分别为每件元和元,现甲销售点需要水果件,乙销售点需要水果件.
设从基地运往甲销售点水果件,总运费为元,请用含的代数式表示,并写出的取值范围;
若总运费不超过元,且基地运往甲销售点的水果不低于件,试确定运费最低的运输方案,并求出最低运费.
24.(9分)如图,的三边长分别为.
求的取值范围;
当的周长为偶数时,求;
若为等腰三角形,求.
25.(9分)已知一次函数,
若函数图象平行于直线,求的值;
若函数值随自变量的增大而减小,求的取值范围:
若函数图象不经过第二象限,求的取值范围.
参考答案
1.B
【分析】
根据一次函数的定义进行选择即可.
【详解】
A.未知数的指数是2,故不符合题意;
B.只含有一个未知数,且未知数的指数是1的等式是一次函数,故符合题意;
C.未知数在分母的位置,故不符合题意;
D.当时,不符合题意;
故答案选B.
【点睛】
本题考查的是一次函数的定义与识别,能够根据定义准确判断出一次函数是解题的关键.
2.C
【解析】
试题分析:利用锐角的性质、偶数的定义、平行线的性质及相反数的定义分别判断后即可确定正确的选项.
A、一个锐角的补角大于这个角,正确,是真命题,不符合题意;
B、凡能被2整除的数,末尾数字必是偶数,正确,是真命题,不符合题意;
C、两条平行直线被第三条直线所截,同旁内角才互补,故错误,是假命题,符合题意;
D、相反数等于他本身的数是0,正确,是真命题,不符合题意
考点:命题与定理.
3.B
【分析】
平面内一点到x轴的距离为该点纵坐标的绝对值,到y轴的距离为该点横坐标的绝对值,因为点M在第四象限,根据第四象限点坐标的特征即可选出答案.
【详解】
设点M的坐标为
∵点到轴距离为2,到轴距离为1
∴
∵点M在第四象限,
∴
∴,
∴点M坐标为(1,-2)
故选B.
【点睛】
本题考查的是平面直角坐标系中点的坐标特征,能够根据第四象限内点的坐标特征确定点M的坐标是解题的关键.
4.A
【分析】
根据一次函数的增减性进行解答即可.
【详解】
∵函数中
∴函数的增减性是y随x的增大而减小
又∵-2<3
∴
故答案选A.
【点睛】
本题考查的是一次函数的性质,能够根据解析式判断出一次函数的增减性是解题的关键.
5.D
【分析】
先根据点A和它的对应点C的坐标之间的变化规律得到图形的变换规律,然后利用此规律写出点B的对应点D的坐标即可.
【详解】
∵点对应点为
∴线段CD是由线段AB先向右平移3-(-1)=4个单位,向上平移5-2=3个单位。
∵点是点的对应点
∴点D的横坐标为-2+4=2,纵坐标为-1+3=2
∴点D的坐标为(2,2)
故答案选D.
【点睛】
本题考查的是图形的平移的特征,能够根据点A与点C的坐标总结出图形的平移规律是解题的关键.
6.C
【分析】
根据等腰三角形的特征和三角形三边之间的关系分2是腰与5是腰两种情况去讨论,即可选出答案.
【详解】
当2是腰,5是底时,三边长分别是2,2,5,因为2+2<5,所以这种情况不能组成三角形;
当5是腰,2是底时,三边长分别是5,5,2,因为2+5>5,符合三角形三边关系,此时三角形的周长为2+5+5=12.
故答案选C.
【点睛】
本题考查的是等腰三角形的性质和三角形三边关系,能够分情况讨论是解题的关键.
7.B
【分析】
根据“一次函数与图象在轴上相交于同一点”,可知两个图像与x轴的交点是同一个点,用a,b分别表示出这个交点的横坐标,然后联立即可.
【详解】
在中,令,得;
在中,令,得
∵一次函数与图象在轴上相交于同一点
∴
∴
故选B.
【点睛】
本题考查的是一次函数同解问题,能够根据图像交点相同想到用同解联立来解答是解题的关键.
8.C
【分析】
根据题干新定义的概念,理解点P的“k属派生点”的概念,设点P的坐标为(a,b),可得,进而选择即可.
【详解】
设点P的坐标为,因为点P的“k属派生点”的坐标满足,
所以
A.3×1+2=5≠12,不符合题意;
B.2×3+1=7≠12,不符合题意;
C.2×3+6=12,符合题意;
D.6×3+2=20≠12不符合题意;
综上答案选C.
【点睛】
本题考查的新定义概念,能够读懂题意是解题的关键.
9.D
【分析】
主要考查了函数的定义.注意函数的意义反映在图象上简单的判断方法是:作垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.
【详解】
A、B、C作垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点,能表示y是x的函数,故不符合题意;
D. 作垂直x轴的直线在左右平移的过程中与函数图象存在2个交点,不能表示y是x的函数,故D符合题意;
故选:D.
【点睛】
此题考查函数的概念,解题关键在于熟悉掌握函数的定义.
10.C
【分析】
根据与x轴平行的直线上点的坐标特征解析判断.
【详解】
∵AD∥BC∥x轴,
∴点A与点D的纵坐标相同,点B与点C的纵坐标相同
故选C.
【点睛】
此题考查坐标与图形性质,解题关键在于熟练分析坐标特征及判断.
11..
【详解】
∵在实数范围内有意义,
∴
∴
故答案为
12.-1
【分析】
根据一次函数的定义可知未知数的指数应该是1,且一次项系数不能为0,据此列式计算即可.
【详解】
根据题意可知,解得,所以,故答案为-1.
【点睛】
本题考查的是一次函数的定义,熟知一次函数的定义是解题的关键.
13.82°
【分析】
根据三角形的内角和是180°进行求解即可.
【详解】
如图,∵AD⊥BC,
∴∠ADC=90°,
又∵∠CAD=22°,
∴∠C=180°-90°-22°=68°,
∴∠BAC=180°-∠B-∠C=180°-30°-68°=82°
故答案为82°.
【点睛】
本题考查的是三角形的内角和定理,能够利用三角形的内角和定理进行解题是关键.
14.
【分析】
根据直线解析式可知直线必过一三象限,当经过点B时b的值最小,当经过点D是b的值最大,由此得出结论即可.
【详解】
∵直线中
∴此直线必过一三象限
∵,
当直线经过点B时,-2+b=-2,解得b=0;
当直线经过点D时,-4+b=-1,解得b=3;
∴
故答案为.
【点睛】
本题考查的是一次函数的实际应用,能够根据题意将问题转换成一次函数问题是解题的关键.
15.且
【分析】
求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件进行求解即可.
【详解】
要使在实数范围内有意义,
必须
所以x≥1且,
故答案为:x≥1且.
【点睛】
本题考查了函数自变量的取值范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.
16.83°
【分析】
由DF⊥AB,在Rt△BDF中可求得∠B;再由∠ACD=∠A+∠B可求得∠ACD的度数.
【详解】
解:∵DF⊥AB,
∴∠B+∠D=90°,
∴∠B=90°-∠D=90°-42°=48°,
∴∠ACD=∠A+∠B=35°+48°=83°.
故答案为83°
【点睛】
本题主要考查了三角形内角和定理以及三角形外角性质的综合应用,解题时注意:三角形内角和是180°,三角形的一个外角等于和它不相邻的两个内角的和.
17.(1)见解析;(2)4
【分析】
(1)根据点A坐标建立坐标系即可,根据平移先找出对应点,然后即可画出图形;
(2)利用割补法即可求面积.
【详解】
解:因为点A(0,3),所以点A在y轴上,据此建立直角坐标系即可,如下图,从而可知点B坐标为(-3,-1),点C坐标为(1,1),根据平移可知A、B、C对应点坐标分别为(3,0)、(-4,0)、(4,-2),描点连线;
(2),故的面积是4.
【点睛】
本题考查的是直角坐标系,平移的性质和三角形面积的求法,能够充分调动所学知识是解题的关键.
18.(1);(2)
【分析】
(1)根据“与成正比例”,设,将,代入求解即可;
(2)将点坐标代入(1)中解析式即可.
【详解】
解:(1)∵与成正比例
∴设
将,代入得,即
∴,即
∴与之间的函数关系式为;
(2)∵点在该函数图象上
将其代入到中有,解得
∴的值是-8.
【点睛】
本题考查的是一次函数问题,能够根据题意列出一次函数式是解题的关键.
19.120°
【分析】
根据∠ABC=66°,∠ACB=54°,先求∠A得度数,再求∠ABE与∠ACF的度数,最后利用三角形的外角定理即可求得答案.
【详解】
解:∵∠ABC=66°,∠ACB=54°
∴∠A=180°-∠ABC-∠ACB=180°-66°-54°=60°
又∵BE是AC边上的高
∴∠AEB=∠BEC=90°
∴∠ABE=180°-∠A-∠AEB=180°-60°-90°=30°
同理∠ACF=30°
∴∠BHC=∠BEC+∠ACF=90°+30°=120°
【点睛】
本题考查了三角形内角和定理和三角形外角定理,能够根据这些知识解答问题是关键.
20.(1)点M不是和谐点,点N是和谐点;(2)的值分别是6,9
【分析】
(1)根据和谐点的定义。利用矩形的面积和周长公式进行证明即可;
(2)利用和谐点的定义列出关于a的方程,由此求a,然后将点P的坐标代入直线方程求解b值即可.
【详解】
解:(1)∵
∴点M不是和谐点,点N是和谐点;
(2)∵点P是和谐点
∴,解得
∴点P的坐标为
∵点P在直线上
∴代入得
解得
∴的值分别是6,9.
【点睛】
本题考查的是新定义和列式计算的能力,能够读懂题意是解题的关键.
21.,100,1;直线CD的解析式为:;两人第二次相遇后,又经过时或时两人相距
【分析】
(1)根据速度和时间列方程:60×1+m=160,可得m=100,根据D的坐标可计算直线OD的解析式,从图中知E的横坐标为2,可得E的坐标,根据点E到D的时间差及速度可得休息的时间;
(2)利用待定系数法求直线CD的解析式;
(3)先计算第二次相遇的时间:y=360时代入y=80x可得x的值,再计算x=5时直线OD的路程,可得路程差为40km,所以存在两种情况:两人相距20km,列方程可得结论.
【详解】
由图形得,
设OD的解析式为:,
把代入得:,,
:,
当时,,
,
由题意得:,,
,
故答案为,100,1;
,,
直线AE:,
当时,,
,
,
,
设CD的解析式为:,
把,代入得:,解得:,
直线CD的解析式为:;
的解析式为:,
当时,,
,
出发5h时两个相距40km,
把代入得:,
出发时两人第二次相遇,
当时,,
,,
当时,,
,,
答:两人第二次相遇后,又经过时或时两人相距
【点睛】
本题考查了一次函数的应用,读懂函数图象,理解横、纵坐标表示的含义,熟练掌握一次函数的相关知识、利用数形结合思想是解题的关键.
22.(1)证明见解析;(2)∠E=10°;(3)∠En+l=∠E.
【分析】
(1)根据三角形的一个外角等于和它不相邻的两个内角的和,得出∠DCE=∠A+∠D,∠DFE=∠DCE+∠E,将第一式代入第二式即可得证;
(2)根据角平分线及三角形外角的性质得出∠ECG=∠DCG=(∠D+∠DBC),∠ECG=∠E+∠EBC=∠E+
∠DBC,则∠D=2∠E,再利用上题结论∠DFE=∠A+∠D+∠E,将已知条件代入,即可求出∠E的度数;
(3)先根据角平分线及三角形外角的性质得出∠E1=∠E,同理得出∠E2=∠E1,则∠E2=∠E=∠E,由此得出规律∠En+l=∠E.
【详解】
(1)证明:∵∠DCE=∠A+∠D,∠DFE=∠DCE+∠E,
∴∠DFE=∠A+∠D+∠E;
(2)解:∵∠DCG=∠D+∠DBC,CE平分∠DCG,
∴∠ECG=∠DCG=(∠D+∠DBC),
∵BE平分∠DBC,
∴∠EBC=∠DBC,
∵∠ECG=∠E+∠EBC=∠E+∠DBC,
∴∠E+∠DBC=(∠D+∠DBC),
∴∠E=∠D,
∴∠D=2∠E.
∵∠DFE=63°,∠A=33°,∠DFE=∠A+∠D+∠E,
∴∠D+∠E=∠DEF-∠A=63°-33°=30°,
∴2∠E+∠E=30°,
∴∠E=10°;
(3)∵∠ECG=∠E+∠EBC,CE1平分∠ECG,
∴∠E1CG=∠ECG=(∠E+∠EBC).
∵BE1平分∠EBC,
∴∠E1BC=∠EBC.
∵∠E1CG=∠E1+∠E1BC=∠E1+∠EBC,
∴∠E1+∠EBC=(∠E+∠EBC),
∴∠E1=∠E.
同理:∠E2=∠E1,
∴∠E2=∠E=∠E,
∴∠En+l=∠E.
【点睛】
此题考查三角形的角平分线,三角形的外角的性质,(3)中得出∠E1=∠E,是解题的关键.
23.(1)W=35x+11200(80≤x≤380);(2)18200元,从A基地运往甲销售点的水果200件,运往乙销售点的水果180件;从B基地运往甲销售点的水果200件,运往乙销售点的水果120件.
【分析】
(1)表示出从A基地运往乙销售点的水果件数,从B基地运往甲、乙两个销售点的水果件数,然后根据运费=单价×数量列式整理即可得解,再根据运输水果的数量不小于0列出不等式求解得到x的取值范围;
(2)根据一次函数的增减性确定出运费最低时的运输方案,然后求解即可.
【详解】
(1)设从A基地运往甲销售点水果x件,则从A基地运往乙销售点的水果(380-x)件,
从B基地运往甲销售点水果(400-x)件,运往乙基地(x-80)件,
由题意得,W=40x+20(380-x)+15(400-x)+30(x-80),
=35x+11200,
即W=35x+11200,
∵ ,
∴80≤x≤380,
即x的取值范围是80≤x≤380;
(2)∵A地运往甲销售点的水果不低于200件,
∴x≥200,
∵k=35>0,
∴运费W随着x的增大而增大,
∴当x=200时,运费最低,为35×200+11200=18200元<18300元,
此时,方案为:
从A基地运往甲销售点的水果200件,运往乙销售点的水果180件,
从B基地运往甲销售点的水果200件,运往乙销售点的水果120件.
【点睛】
此题考查一次函数的应用,一元一次不等式组的应用,读懂题目信息,准确表示出从A、B两个基地运往甲、乙两个销售点的水果的件数是解题的关键.
24.(1)4<x<14;(2)x=6、8、10,12;(3)x=5或9.
【分析】
(1)根据三角形的第三边大于两边之差,而小于两边之和进行计算;
(2)要使周长是偶数,因为其它两边之和是13,则x应是奇数;
(3)根据等腰三角形的定义:有两边相等的三角形是等腰三角形,则x=4或9,再根据(1)中的取值范围进行取舍.
【详解】
△ABC的三边长分别为5、9、x,
(1)根据三角形的第三边大于两边之差,而小于两边之和,得9-5<x<9+5,即4<x<14;
(2)因为已知的两边之和是14,为偶数,要使周长为偶数,则第三边应是偶数,即x=6、8、10,12;
(3)若△ABC为等腰三角形,x=5或9.
【点睛】
此题考查三角形的三边关系,理解数的奇偶性,理解等腰三角形的性质,解题关键在于注意一定要检查是否符合三角形的三边关系.
25.(1)m=-1;(2)m<-;(3)-<m≤1.
【分析】
(1)根据两直线平行的性质求出m的值;
(2)根据一次函数的性质列出关于m的不等式求出m的取值范围即可;
(3)根据一次函数的性质列出关于m的不等式组求出m的取值范围即可.
【详解】
(1)∵函数图象平行于直线y=x+1,
∴2m+3=1,解得m=-1;
(2)∵该函数的值y随自变量x的增大而减小,
∴2m+3<0,解得m<-;
(3)∵该函数图象不经过第二象限,
∴ ,解得-<m≤1.
【点睛】
此题考查一次函数的性质,熟知一次函数的图象与系数的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
