沪科版八年级上册数学期中考试试题(含解析)
文档属性
| 名称 | 沪科版八年级上册数学期中考试试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
沪科版八年级上册数学期中考试试卷
一、选择题:本大题共12小题,每小题3分,共36分。
1.下列语句是命题的是 ( )
A.请借我100元钱 B.你运动了吗 C.连接A, B两点 D.华盛顿是日本首都
2.若m<0,则点M(m,-1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系中,点P (3, -2)先向右平移3个单位,再向下平移2个单位,得到的点坐标是( )
A.(0, 0) B.(6,-4) C.(6,0) D.(0,-4)
4.下列各点在直线y= - 2x+8 上的是( )
A.(5,-2) B.(-3, 2) C.(2,-2) D.(0,- 8)
5.下列式子中,不是的函数的是( )
A. B. C. D.
6.将一次函数y= - 3x+1的图象沿x轴向左平移2个单位长度后,得到的新的图象对应的函数关系式为( )
A.y= - 3x+7 B.y= -3x- 5 C.y=-3x- 1 D.y= - 3x+3
7.已知一个三角形的两条边长分别为3和7,则第三条边的长度不能是( )
A.10 B.9 C.8 D.7
8.如图,函数 y1=﹣2x 与 y2=ax+3 的图象相交于点 A(m,2),则关于 x 的不等式﹣2x>ax+3 的解集是( )
A.x>2 B.x<2 C.x>﹣1 D.x<﹣1
9.无论a取何值时点P (a+1, 2a-4), 都不可能在第( )象限.
A.一 B.二 C.三 D.四
10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形EFGC,动点P从点A出发,沿A→E→F→G→C→B的路线,绕多边形的边匀速运动到点B时停止,则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B. C. D.
11.将一次函数y=2x-3的图象沿y轴向上平移8个单位长度,所得直线的解析式为()
A.y=2x-5 B.y=2x+5 C.y=2x+8 D.y=2x-8
12.在同一平面直角坐标系中,直线与直线的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题:本大题共4小题,每小题3分,共12分。
13.直线y=x-3不经过第_______________象限.
14.若P(2+a,-1-2a)到两坐标轴的距离相等,则点P的坐标是______________ .
15.同学们学习了一次函数以后,我们知道一次函数的图像是一条直线,我们到九年级还会学习二次函数,二次函数的图像将是一条抛物线, 其形状就像抛出去的物体,存在最高点(或最低点)我们称之为抛物线的顶点,已知抛物线y= - 2(x-m-1)2+2m -1顶点坐标为(m+1,2m- 1)无论取何值,其顶点坐标一定在一次函数____________________ .
16.一次函数的图象经过点,且与轴、轴分别交于点、,则的面积等于___________.
三、解答题:本大题共9小题,共72分。
17.(8分)平面直角坐标系中,有一点P(-m+1, 2m-6), 试求满足下列条件的m的值,
(1)点P在x轴上:
(2)点P在第三象限:
(3)点P到y轴距离是1.
18.(8分)如图,在△ABC中, BE是AC边上的高,DE∥BC, ∠ADE=52° ,∠C=68°,求∠ABE的度数.
19.已知y是x的正比例函数,并且当x=-2时,y=6.
(1)求y关于x的函数解析式:
(2)当y=3时,求x的值.
20.(8分)4月23日是“世界读书日”,甲、乙两个书店在这一天举行了购书优惠活动.甲书店:所有书籍按标价8折出售;乙书店:一次购书中标价总额不超过100元的按原价计费,超过100元后的部分打6折.
(1)以x(单位:元)表示标价总额,y(单位:元)表示应支付金额,分别就两家书店的优惠方式,求y关于x的函数解析式;
(2)“世界读书日”这一天,如何选择这两家书店去购书更省钱?
21.(8分)已知:一次函数 y=kx+b与y=3x在同平面直角坐标系内平行,当x=1时,y=0.
(1)求y与x之间的函数解析式:
(2)若点P (a, 9)、Q (1,b)均在该函数图象上,则a= , b= , ab= ;
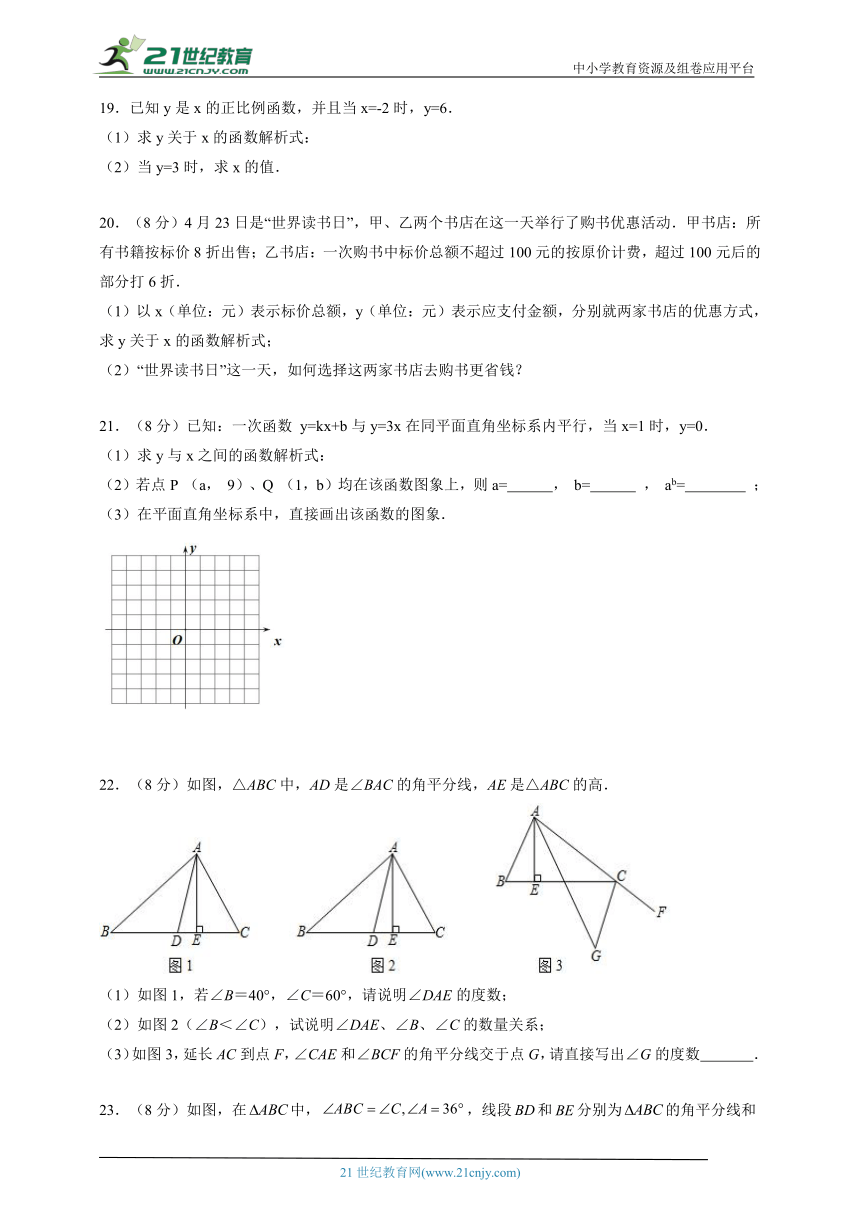
(3)在平面直角坐标系中,直接画出该函数的图象.
22.(8分)如图,△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=60°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,请直接写出∠G的度数 .
23.(8分)如图,在中,,线段和分别为的角平分线和高线.求、的大小.
24.(8分)已知一次函数的图象与直线平行,且与轴交于点
(1)求该一次函数的函数表达式;
(2)根据(1)的结果,对于,请说明随的变化情况;
(3)若一次函数图象上有两点、,,求的值;
25.(8分)小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了研究,下面是小慧的研究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.其中,b= ;
x … ﹣1 0 2 3 …
y … b 0 2 …
(3)在平面直角坐标系xoy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .
参考答案
1.D
【分析】
根据命题的定义解答即可.
【详解】
解:A、请借我100元钱是祈使句,没有对事情做出判断,不是命题,故本选项不符合题意;
B、你运动了吗是疑问句,没有对事情做出判断,不是命题,故本选项不符合题意;
C、连接A,B两点,是叙述句,没有对事情作出判断,不是命题,故本选项不符合题意;
D、华盛顿是日本首都,对事情做出了判断,是命题,故本选项符合题意;
故选:D.
【点睛】
本题考查命题的定义,记住命题是判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.
2.C
【分析】
由于m<0,点M坐标为(m,-1),得到点M的横坐标为负数,纵坐标为负数,然后根据各象限点的坐标特点即可得到正确答案.
【详解】
解:∵m<0,-1<0,
即点M的横坐标为负数,纵坐标为负数,
所以点M在第三象限.
故选:C.
【点睛】
本题考查了坐标:直角坐标系中点与有序实数对一一对应;在x轴上点的纵坐标为0,在y轴上点的横坐标为0;记住各象限点的坐标特点.
3.B
【分析】
直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
【详解】
解:原来点的横坐标是3,纵坐标是-2,向右平移3个单位再向下平移2个单位得到新点的横坐标是3+3=6,纵坐标为-2-2=-4.
则新坐标为(6,-4).
故选:B.
【点睛】
本题主要考查了平移中点的变化规律:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
4.A
【分析】
分别代入x=5,x=-3,x=2和x=0,求出与之对应的y值,再对照四个选项即可得出结论.
【详解】
解:当x=5时,y=-2x+8=-2,
∴点(5,-2)在函数y=-2x+8的图象上;
当x=-3时,y=-2x+8=14,
当x=2时,y=-2x+8=4,
当x=0时,y=-2x+8=8,
∴点(-3,2)、点(2,-2)和点(0,-8)不在函数y=-2x+8的图象上;
故选:A.
【点睛】
本题考查了一次函数图象上点的坐标特征,牢记直线上任意一点的坐标都满足函数关系式y=kx+b是解题的关键.
5.D
【分析】
利用函数定义可得答案.
【详解】
解:、,是的函数,故此选项不合题意;
、,是的函数,故此选项不合题意;
、,是的函数,故此选项不合题意;
、,不是的函数,故此选项符合题意;
故选:.
【点睛】
此题主要考查了函数的概念,对于函数概念的理解:①有两个变量;②一个变量的数值随着另一个变量的数值的变化而发生变化;③对于自变量的每一个确定的值,函数值有且只有一个值与之对应,即单对应.
6.B
【分析】
直接利用一次函数平移规律“上加下减”、“左加右减”即可得到答案.
【详解】
解:将一次函数y=-3x+1的图象沿x轴向左平移2个单位长度,
平移后所得图象对应的函数关系式为:y=-3(x+2)+1,
即y=-3x-5.
故选:B.
【点睛】
本题主要考查了一次函数平移规律,掌握一次函数平移规律“左加右减,上加下减”是解题的关键.
7.A
【分析】
设第三边长为x,然后再利用三边关系列出不等式,进而可得答案.
【详解】
解:设第三边长为x,由题意得:
7-3<x<7+3,
即:4<x<10,
故选:A.
【点睛】
此题主要考查了三角形的三边关系,关键是掌握三角形两边之和大于第三边.三角形的两边差小于第三边.
8.D
【详解】
因为函数与的图象相交于点A(m,2),把点A代入可求出,所以点A(-1,2),然后把点A代入解得, 不等式,
可化为,解不等式可得:,故选D.
9.B
【分析】
确定P点位置只需判定(a+1)和(2a-4)的符号即可.所以需分段讨论.
【详解】
解:若a+1>0,2a-4>0,即a>2,此时点P在第一象限;
若a+1>0,2a-4<0,即-1若a+1<0,2a-4<0,即a<-1,此时点P在第三象限;
若a+1<0,2a-4>0,无解;
∴点P不可能在第二象限,
故选B.
【点睛】
本题主要考查点的坐标,解不等式组,解题的关键是掌握各象限内点的坐标符号特点.
10.B
【分析】
用面积公式计算出点P在线段运动的函数表达式,即可求解.
【详解】
解:①当点P在AE上运动时,S=×AB×AP=×2×t=t;
②当点P在EF上运动时,S=×1×2=1;
③当点P在FG上运动时,S=×2×(t-1)=t-1;
④当点P在GC上运动时,同理S=2;
⑤当点P在BC上运动时,同理可得:函数的表达式为一次函数,图象为线段;
故选:B.
【点睛】
本题是运动型综合题,解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.
11.B
【分析】
根据函数图象上加下减,可得答案.
【详解】
解:由题意,得:y=2x﹣3+8,
即y=2x+5,
故选B.
【点睛】
本题考查了一次函数图象与几何变换,利用函数图象的平移规律是解题关键.
12.D
【详解】
试题分析:直线y=4x+1过一、二、三象限;
当b>0时,直线y=﹣x+b过一、二、四象限,
两直线交点可能在一或二象限;
当b<0时,直线y=﹣x+b过二、三、四象限,
两直线交点可能在二或三象限;
综上所述,直线y=4x+1与直线y=﹣x+b的交点不可能在第四象限,
故选D.
考点:两条直线相交或平行问题.
13.二
【分析】
由,,利用一次函数图象与系数的关系可得出直线经过第一、三、四象限,即直线不经过第二象限.
【详解】
解:,,
直线经过第一、三、四象限,
直线不经过第二象限.
故答案为:二.
【点睛】
本题考查了一次函数图象与系数的关系,牢记“k>0,b<0 y=kx+b的图象在一、三、四象限”是解题的关键.
14.(1,1)或(3,-3)
【分析】
分横坐标和纵坐标相等和互为相反数两种情况讨论求解.
【详解】
解:∵点P(2+a,-1-2a)到两坐标轴的距离相等,
∴2+a=-1-2a,
解得a=-1,
此时2+a=2+(-1)=1,则点P(1,1),
或2+a-1-2a=0,
解得a=1,
此时,2+a=2+1=3,-1-2a=-1-2=-3,则点P(3,-3),
故答案为(1,1)或(3,-3).
【点睛】
本题考查了点的坐标,是基础题,难点在于要分情况讨论.
15.
【分析】
根据顶点坐标设x=m+1,y=2m-1,分别用x和y表示出m,得到关于x和y的等式,变形即可.
【详解】
解:∵抛物线的顶点为(m+1,2m-1),
令x=m+1,y=2m-1,
则m=x-1,m=,
∴,
变形得:,
故答案为:.
【点睛】
本题考查了一次函数图像上的点,解题的关键是用x和y表示出m,得到关于x和y的等式.
16.
【解析】
∵一次函数y= 2x+m的图象经过点P( 2,3),
∴3=4+m,
解得m= 1,
∴y= 2x 1,
∵当x=0时,y= 1,
∴与y轴交点B(0, 1),
∵当y=0时,x= ,
∴与x轴交点A( ,0),
∴△AOB的面积:×1×=.
故答案为.
点睛:首先根据待定系数法求得一次函数的解析式,然后计算出与x轴交点,与y轴交点的坐标,再利用三角形的面积公式计算出面积即可.
17.(1)m=3;(2)1【分析】
(1)点P在x轴上,该点的纵坐标为0;
(2)根据第三象限的点的横坐标小于0,纵坐标小于0解答即可;
(3)根据点到y轴的距离为1,则该点的横坐标的绝对值为1,据此计算即可.
【详解】
解:(1)要使点P在x轴上,m应满足2m-6=0,解得m=3,
所以,当m=3时,点P在x轴上;
(2)要使点P在第三象限,m应满足,
解得:1所以,当1(3)要使点P到y轴距离是1,m应满足|-m+1|=1,
解得m=2或m=0,
所以,当m=2或m=0时,点M到y轴距离是1.
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
18.30°
【分析】
利用平行线的性质定理可得∠ABC=∠ADE=52°,由三角形的内角和定理可得∠EBC的度数,可得∠ABE.
【详解】
解:∵DE∥BC,∠ADE=52°,
∴∠ABC=∠ADE=52°,
∵BE是AC边上的高,
∴∠BEC=90°,
∵∠C=68°,
∴∠EBC=90-∠C=22°,
∴∠ABE=∠ABC-∠EBC=52°-22°=30°.
【点睛】
本题主要考查了平行线的性质定理和三角形的内角和定理,熟练掌握定理是解答此题的关键.
19.(1)y=-3x;(2)-1
【分析】
(1)根据y与x成正比例关系设出函数的解析式,再把当x=-2时,y=6代入函数解析式即可求出k的值,进而求出y与x之间的函数解析式.
(2)根据(1)中所求函数解析式,将y=3代入其中,求得x值.
【详解】
解:(1)设y=kx(k≠0).
将x=-2,y=6代入得:6=-2k,
所以,k=-3,
所以,y关于x的函数解析式为y=-3x;
(2)由(1)知,y=-3x,
∴当y=3时,3=-3x,
即x=-1.
【点睛】
本题主要考查了待定系数法求一次函数的解析式、函数值.利用待定系数法求一次函数的解析式,通常先设出一次函数的关系式y=kx+b(k≠0),将已知两点的坐标代入求出k、b的值,再根据一次函数的性质求解.
20.(1)y=0.8x; (2)见解析
【分析】
(1)根据题意给出的等量关系即可求出答案.
(2)先求出两书店所需费用相同时的书本数量,从而可判断哪家书店省钱.
【详解】
解:(1)甲书店:y=0.8x,
乙书店:当时,y=x,
当时,y=100+0.6(x-100)=0.6x+40,
乙书店:.
(2)令0.8x=0.6x+40,
解得:x=200,
当x<200时,选择甲书店更省钱,
当x=200,甲乙书店所需费用相同,
当x>200,选择乙书店更省钱.
【点睛】
本题考查一次函数和不等式的应用,解题的关键是正确找出题中的等量关系.
21.(1)y=3x-3;(2)4,0,1;(3)见解析
【分析】
(1)根据两直线平行可得k值,再将x=1,y=0代入,得出b值即可;
(2)分别将点P(a,9)、Q(1,b)代入(1)中所求解析式,可得结果;
(3)根据一次函数图象的性质,画出函数图象.
【详解】
解:(1)∵一次函数 y=kx+b与y=3x在同平面直角坐标系内平行,
∴k=3,
∵当x=1时,y=0,
∴0=3+b,
解得:b=-3,
∴y与x之间的函数解析式为y=3x-3;
(2)∵点P(a,9)、Q(1,b)均在该函数图象上,
∴9=3a-3,b=3×1-3,
解得:a=4,b=0,
∴ab=1;
(3)如图所示:
【点睛】
本题考查了待定系数法确定函数解析式及描点法画函数图象,掌握函数图象上的点和函数的关系是解决本题的关键.
22.(1)∠DAE=10°;(2)∠DAE=∠C﹣∠B;(3)45°.
【分析】
(1)先根据三角形的内角和定理求得、,再根据角平分线的定义得到,最后根据角的和差解答即可;
(2)先根据三角形的内角和定理求得、,再根据角平分线的定义得到,然后根据角的和差表示出来即可;
(3)先根据角平分线的定义得到,再结合三角形外角的性质得到,然后根据题意得到,最后算出∠G即可.
【详解】
解:(1)
是的高,
是的角平分线,
,
.
(2)
是的高,
是的角平分线,
,
即;
(3)和的角平分线交于点,
,即,
是的高,
,
.
故答案为:45°.
【点睛】
本题主要考查了三角形内角和定理、角平分线的定义、三角形外角的性质等知识点,灵活应用相关知识成为解答本题的关键.
23.∠ADB=108°,∠DBE=18°.
【解析】
分析:根据三角形的内角和定理,求得,的度数,再利用角平分线的性质求得的度数,再利用高线的性质和三角形的内角和定理求出的度数即可.
本题解析:
因为在中,,
由三角形内角和为,可得
因为线段为的角平分线,所以,
在中,由三角形内角和为,可得 ,
因为线段为的高线,所以
在中,由三角形内角和为,可得 ,
所以
24.(1)(2)随的增大而增大(3)
【解析】
分析:(1)根据两直线平行,则函数解析式的一次项系数相同,即可确定k的值,把(5,0)的坐标代入求得b,求出即可.(2)根据一次函数的性质解答即可;(3)联立方程组解答即可.
本题解析:
(1)因为一次函数的图象与直线平行,
所以
又因为一次函数的图象与轴交于点
所以有,即可得
该一次函数的函数表达式为
(2)随的增大而增大
(3)因为点、在函数图象上,
所以有
两式相减,得
所以
点睛:此题考查两直线平行问题,关键是根据两直线平行的特点解答.
25.(1)x为任意实数,(2)2,(3)见解析,(4)函数的最小值为0(答案不唯一).
【解析】
【分析】
(1)根据一次函数的性质即可得出结论;
(2)把x=﹣1代入函数解析式,求出y的值即可;
(3)在坐标系内描出各点,再顺次连接即可;
(4)根据函数图象即可得出结论.
【详解】
(1)∵x无论为何值,函数均有意义,
∴x为任意实数.
故答案为:任意实数;
(2)∵当x=﹣1时,y=|﹣1﹣1|=2,
∴b=2.
故答案为:2;
(3)如图所示;
(4)由函数图象可知,函数的最小值为0.
故答案为:函数的最小值为0(答案不唯一).
【点睛】
本题考查的是一次函数的性质,根据题意画出函数图象,利用数形结合求解是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版八年级上册数学期中考试试卷
一、选择题:本大题共12小题,每小题3分,共36分。
1.下列语句是命题的是 ( )
A.请借我100元钱 B.你运动了吗 C.连接A, B两点 D.华盛顿是日本首都
2.若m<0,则点M(m,-1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系中,点P (3, -2)先向右平移3个单位,再向下平移2个单位,得到的点坐标是( )
A.(0, 0) B.(6,-4) C.(6,0) D.(0,-4)
4.下列各点在直线y= - 2x+8 上的是( )
A.(5,-2) B.(-3, 2) C.(2,-2) D.(0,- 8)
5.下列式子中,不是的函数的是( )
A. B. C. D.
6.将一次函数y= - 3x+1的图象沿x轴向左平移2个单位长度后,得到的新的图象对应的函数关系式为( )
A.y= - 3x+7 B.y= -3x- 5 C.y=-3x- 1 D.y= - 3x+3
7.已知一个三角形的两条边长分别为3和7,则第三条边的长度不能是( )
A.10 B.9 C.8 D.7
8.如图,函数 y1=﹣2x 与 y2=ax+3 的图象相交于点 A(m,2),则关于 x 的不等式﹣2x>ax+3 的解集是( )
A.x>2 B.x<2 C.x>﹣1 D.x<﹣1
9.无论a取何值时点P (a+1, 2a-4), 都不可能在第( )象限.
A.一 B.二 C.三 D.四
10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形EFGC,动点P从点A出发,沿A→E→F→G→C→B的路线,绕多边形的边匀速运动到点B时停止,则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B. C. D.
11.将一次函数y=2x-3的图象沿y轴向上平移8个单位长度,所得直线的解析式为()
A.y=2x-5 B.y=2x+5 C.y=2x+8 D.y=2x-8
12.在同一平面直角坐标系中,直线与直线的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题:本大题共4小题,每小题3分,共12分。
13.直线y=x-3不经过第_______________象限.
14.若P(2+a,-1-2a)到两坐标轴的距离相等,则点P的坐标是______________ .
15.同学们学习了一次函数以后,我们知道一次函数的图像是一条直线,我们到九年级还会学习二次函数,二次函数的图像将是一条抛物线, 其形状就像抛出去的物体,存在最高点(或最低点)我们称之为抛物线的顶点,已知抛物线y= - 2(x-m-1)2+2m -1顶点坐标为(m+1,2m- 1)无论取何值,其顶点坐标一定在一次函数____________________ .
16.一次函数的图象经过点,且与轴、轴分别交于点、,则的面积等于___________.
三、解答题:本大题共9小题,共72分。
17.(8分)平面直角坐标系中,有一点P(-m+1, 2m-6), 试求满足下列条件的m的值,
(1)点P在x轴上:
(2)点P在第三象限:
(3)点P到y轴距离是1.
18.(8分)如图,在△ABC中, BE是AC边上的高,DE∥BC, ∠ADE=52° ,∠C=68°,求∠ABE的度数.
19.已知y是x的正比例函数,并且当x=-2时,y=6.
(1)求y关于x的函数解析式:
(2)当y=3时,求x的值.
20.(8分)4月23日是“世界读书日”,甲、乙两个书店在这一天举行了购书优惠活动.甲书店:所有书籍按标价8折出售;乙书店:一次购书中标价总额不超过100元的按原价计费,超过100元后的部分打6折.
(1)以x(单位:元)表示标价总额,y(单位:元)表示应支付金额,分别就两家书店的优惠方式,求y关于x的函数解析式;
(2)“世界读书日”这一天,如何选择这两家书店去购书更省钱?
21.(8分)已知:一次函数 y=kx+b与y=3x在同平面直角坐标系内平行,当x=1时,y=0.
(1)求y与x之间的函数解析式:
(2)若点P (a, 9)、Q (1,b)均在该函数图象上,则a= , b= , ab= ;
(3)在平面直角坐标系中,直接画出该函数的图象.
22.(8分)如图,△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=60°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,请直接写出∠G的度数 .
23.(8分)如图,在中,,线段和分别为的角平分线和高线.求、的大小.
24.(8分)已知一次函数的图象与直线平行,且与轴交于点
(1)求该一次函数的函数表达式;
(2)根据(1)的结果,对于,请说明随的变化情况;
(3)若一次函数图象上有两点、,,求的值;
25.(8分)小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了研究,下面是小慧的研究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.其中,b= ;
x … ﹣1 0 2 3 …
y … b 0 2 …
(3)在平面直角坐标系xoy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .
参考答案
1.D
【分析】
根据命题的定义解答即可.
【详解】
解:A、请借我100元钱是祈使句,没有对事情做出判断,不是命题,故本选项不符合题意;
B、你运动了吗是疑问句,没有对事情做出判断,不是命题,故本选项不符合题意;
C、连接A,B两点,是叙述句,没有对事情作出判断,不是命题,故本选项不符合题意;
D、华盛顿是日本首都,对事情做出了判断,是命题,故本选项符合题意;
故选:D.
【点睛】
本题考查命题的定义,记住命题是判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.
2.C
【分析】
由于m<0,点M坐标为(m,-1),得到点M的横坐标为负数,纵坐标为负数,然后根据各象限点的坐标特点即可得到正确答案.
【详解】
解:∵m<0,-1<0,
即点M的横坐标为负数,纵坐标为负数,
所以点M在第三象限.
故选:C.
【点睛】
本题考查了坐标:直角坐标系中点与有序实数对一一对应;在x轴上点的纵坐标为0,在y轴上点的横坐标为0;记住各象限点的坐标特点.
3.B
【分析】
直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
【详解】
解:原来点的横坐标是3,纵坐标是-2,向右平移3个单位再向下平移2个单位得到新点的横坐标是3+3=6,纵坐标为-2-2=-4.
则新坐标为(6,-4).
故选:B.
【点睛】
本题主要考查了平移中点的变化规律:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
4.A
【分析】
分别代入x=5,x=-3,x=2和x=0,求出与之对应的y值,再对照四个选项即可得出结论.
【详解】
解:当x=5时,y=-2x+8=-2,
∴点(5,-2)在函数y=-2x+8的图象上;
当x=-3时,y=-2x+8=14,
当x=2时,y=-2x+8=4,
当x=0时,y=-2x+8=8,
∴点(-3,2)、点(2,-2)和点(0,-8)不在函数y=-2x+8的图象上;
故选:A.
【点睛】
本题考查了一次函数图象上点的坐标特征,牢记直线上任意一点的坐标都满足函数关系式y=kx+b是解题的关键.
5.D
【分析】
利用函数定义可得答案.
【详解】
解:、,是的函数,故此选项不合题意;
、,是的函数,故此选项不合题意;
、,是的函数,故此选项不合题意;
、,不是的函数,故此选项符合题意;
故选:.
【点睛】
此题主要考查了函数的概念,对于函数概念的理解:①有两个变量;②一个变量的数值随着另一个变量的数值的变化而发生变化;③对于自变量的每一个确定的值,函数值有且只有一个值与之对应,即单对应.
6.B
【分析】
直接利用一次函数平移规律“上加下减”、“左加右减”即可得到答案.
【详解】
解:将一次函数y=-3x+1的图象沿x轴向左平移2个单位长度,
平移后所得图象对应的函数关系式为:y=-3(x+2)+1,
即y=-3x-5.
故选:B.
【点睛】
本题主要考查了一次函数平移规律,掌握一次函数平移规律“左加右减,上加下减”是解题的关键.
7.A
【分析】
设第三边长为x,然后再利用三边关系列出不等式,进而可得答案.
【详解】
解:设第三边长为x,由题意得:
7-3<x<7+3,
即:4<x<10,
故选:A.
【点睛】
此题主要考查了三角形的三边关系,关键是掌握三角形两边之和大于第三边.三角形的两边差小于第三边.
8.D
【详解】
因为函数与的图象相交于点A(m,2),把点A代入可求出,所以点A(-1,2),然后把点A代入解得, 不等式,
可化为,解不等式可得:,故选D.
9.B
【分析】
确定P点位置只需判定(a+1)和(2a-4)的符号即可.所以需分段讨论.
【详解】
解:若a+1>0,2a-4>0,即a>2,此时点P在第一象限;
若a+1>0,2a-4<0,即-1
若a+1<0,2a-4>0,无解;
∴点P不可能在第二象限,
故选B.
【点睛】
本题主要考查点的坐标,解不等式组,解题的关键是掌握各象限内点的坐标符号特点.
10.B
【分析】
用面积公式计算出点P在线段运动的函数表达式,即可求解.
【详解】
解:①当点P在AE上运动时,S=×AB×AP=×2×t=t;
②当点P在EF上运动时,S=×1×2=1;
③当点P在FG上运动时,S=×2×(t-1)=t-1;
④当点P在GC上运动时,同理S=2;
⑤当点P在BC上运动时,同理可得:函数的表达式为一次函数,图象为线段;
故选:B.
【点睛】
本题是运动型综合题,解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.
11.B
【分析】
根据函数图象上加下减,可得答案.
【详解】
解:由题意,得:y=2x﹣3+8,
即y=2x+5,
故选B.
【点睛】
本题考查了一次函数图象与几何变换,利用函数图象的平移规律是解题关键.
12.D
【详解】
试题分析:直线y=4x+1过一、二、三象限;
当b>0时,直线y=﹣x+b过一、二、四象限,
两直线交点可能在一或二象限;
当b<0时,直线y=﹣x+b过二、三、四象限,
两直线交点可能在二或三象限;
综上所述,直线y=4x+1与直线y=﹣x+b的交点不可能在第四象限,
故选D.
考点:两条直线相交或平行问题.
13.二
【分析】
由,,利用一次函数图象与系数的关系可得出直线经过第一、三、四象限,即直线不经过第二象限.
【详解】
解:,,
直线经过第一、三、四象限,
直线不经过第二象限.
故答案为:二.
【点睛】
本题考查了一次函数图象与系数的关系,牢记“k>0,b<0 y=kx+b的图象在一、三、四象限”是解题的关键.
14.(1,1)或(3,-3)
【分析】
分横坐标和纵坐标相等和互为相反数两种情况讨论求解.
【详解】
解:∵点P(2+a,-1-2a)到两坐标轴的距离相等,
∴2+a=-1-2a,
解得a=-1,
此时2+a=2+(-1)=1,则点P(1,1),
或2+a-1-2a=0,
解得a=1,
此时,2+a=2+1=3,-1-2a=-1-2=-3,则点P(3,-3),
故答案为(1,1)或(3,-3).
【点睛】
本题考查了点的坐标,是基础题,难点在于要分情况讨论.
15.
【分析】
根据顶点坐标设x=m+1,y=2m-1,分别用x和y表示出m,得到关于x和y的等式,变形即可.
【详解】
解:∵抛物线的顶点为(m+1,2m-1),
令x=m+1,y=2m-1,
则m=x-1,m=,
∴,
变形得:,
故答案为:.
【点睛】
本题考查了一次函数图像上的点,解题的关键是用x和y表示出m,得到关于x和y的等式.
16.
【解析】
∵一次函数y= 2x+m的图象经过点P( 2,3),
∴3=4+m,
解得m= 1,
∴y= 2x 1,
∵当x=0时,y= 1,
∴与y轴交点B(0, 1),
∵当y=0时,x= ,
∴与x轴交点A( ,0),
∴△AOB的面积:×1×=.
故答案为.
点睛:首先根据待定系数法求得一次函数的解析式,然后计算出与x轴交点,与y轴交点的坐标,再利用三角形的面积公式计算出面积即可.
17.(1)m=3;(2)1
(1)点P在x轴上,该点的纵坐标为0;
(2)根据第三象限的点的横坐标小于0,纵坐标小于0解答即可;
(3)根据点到y轴的距离为1,则该点的横坐标的绝对值为1,据此计算即可.
【详解】
解:(1)要使点P在x轴上,m应满足2m-6=0,解得m=3,
所以,当m=3时,点P在x轴上;
(2)要使点P在第三象限,m应满足,
解得:1
解得m=2或m=0,
所以,当m=2或m=0时,点M到y轴距离是1.
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
18.30°
【分析】
利用平行线的性质定理可得∠ABC=∠ADE=52°,由三角形的内角和定理可得∠EBC的度数,可得∠ABE.
【详解】
解:∵DE∥BC,∠ADE=52°,
∴∠ABC=∠ADE=52°,
∵BE是AC边上的高,
∴∠BEC=90°,
∵∠C=68°,
∴∠EBC=90-∠C=22°,
∴∠ABE=∠ABC-∠EBC=52°-22°=30°.
【点睛】
本题主要考查了平行线的性质定理和三角形的内角和定理,熟练掌握定理是解答此题的关键.
19.(1)y=-3x;(2)-1
【分析】
(1)根据y与x成正比例关系设出函数的解析式,再把当x=-2时,y=6代入函数解析式即可求出k的值,进而求出y与x之间的函数解析式.
(2)根据(1)中所求函数解析式,将y=3代入其中,求得x值.
【详解】
解:(1)设y=kx(k≠0).
将x=-2,y=6代入得:6=-2k,
所以,k=-3,
所以,y关于x的函数解析式为y=-3x;
(2)由(1)知,y=-3x,
∴当y=3时,3=-3x,
即x=-1.
【点睛】
本题主要考查了待定系数法求一次函数的解析式、函数值.利用待定系数法求一次函数的解析式,通常先设出一次函数的关系式y=kx+b(k≠0),将已知两点的坐标代入求出k、b的值,再根据一次函数的性质求解.
20.(1)y=0.8x; (2)见解析
【分析】
(1)根据题意给出的等量关系即可求出答案.
(2)先求出两书店所需费用相同时的书本数量,从而可判断哪家书店省钱.
【详解】
解:(1)甲书店:y=0.8x,
乙书店:当时,y=x,
当时,y=100+0.6(x-100)=0.6x+40,
乙书店:.
(2)令0.8x=0.6x+40,
解得:x=200,
当x<200时,选择甲书店更省钱,
当x=200,甲乙书店所需费用相同,
当x>200,选择乙书店更省钱.
【点睛】
本题考查一次函数和不等式的应用,解题的关键是正确找出题中的等量关系.
21.(1)y=3x-3;(2)4,0,1;(3)见解析
【分析】
(1)根据两直线平行可得k值,再将x=1,y=0代入,得出b值即可;
(2)分别将点P(a,9)、Q(1,b)代入(1)中所求解析式,可得结果;
(3)根据一次函数图象的性质,画出函数图象.
【详解】
解:(1)∵一次函数 y=kx+b与y=3x在同平面直角坐标系内平行,
∴k=3,
∵当x=1时,y=0,
∴0=3+b,
解得:b=-3,
∴y与x之间的函数解析式为y=3x-3;
(2)∵点P(a,9)、Q(1,b)均在该函数图象上,
∴9=3a-3,b=3×1-3,
解得:a=4,b=0,
∴ab=1;
(3)如图所示:
【点睛】
本题考查了待定系数法确定函数解析式及描点法画函数图象,掌握函数图象上的点和函数的关系是解决本题的关键.
22.(1)∠DAE=10°;(2)∠DAE=∠C﹣∠B;(3)45°.
【分析】
(1)先根据三角形的内角和定理求得、,再根据角平分线的定义得到,最后根据角的和差解答即可;
(2)先根据三角形的内角和定理求得、,再根据角平分线的定义得到,然后根据角的和差表示出来即可;
(3)先根据角平分线的定义得到,再结合三角形外角的性质得到,然后根据题意得到,最后算出∠G即可.
【详解】
解:(1)
是的高,
是的角平分线,
,
.
(2)
是的高,
是的角平分线,
,
即;
(3)和的角平分线交于点,
,即,
是的高,
,
.
故答案为:45°.
【点睛】
本题主要考查了三角形内角和定理、角平分线的定义、三角形外角的性质等知识点,灵活应用相关知识成为解答本题的关键.
23.∠ADB=108°,∠DBE=18°.
【解析】
分析:根据三角形的内角和定理,求得,的度数,再利用角平分线的性质求得的度数,再利用高线的性质和三角形的内角和定理求出的度数即可.
本题解析:
因为在中,,
由三角形内角和为,可得
因为线段为的角平分线,所以,
在中,由三角形内角和为,可得 ,
因为线段为的高线,所以
在中,由三角形内角和为,可得 ,
所以
24.(1)(2)随的增大而增大(3)
【解析】
分析:(1)根据两直线平行,则函数解析式的一次项系数相同,即可确定k的值,把(5,0)的坐标代入求得b,求出即可.(2)根据一次函数的性质解答即可;(3)联立方程组解答即可.
本题解析:
(1)因为一次函数的图象与直线平行,
所以
又因为一次函数的图象与轴交于点
所以有,即可得
该一次函数的函数表达式为
(2)随的增大而增大
(3)因为点、在函数图象上,
所以有
两式相减,得
所以
点睛:此题考查两直线平行问题,关键是根据两直线平行的特点解答.
25.(1)x为任意实数,(2)2,(3)见解析,(4)函数的最小值为0(答案不唯一).
【解析】
【分析】
(1)根据一次函数的性质即可得出结论;
(2)把x=﹣1代入函数解析式,求出y的值即可;
(3)在坐标系内描出各点,再顺次连接即可;
(4)根据函数图象即可得出结论.
【详解】
(1)∵x无论为何值,函数均有意义,
∴x为任意实数.
故答案为:任意实数;
(2)∵当x=﹣1时,y=|﹣1﹣1|=2,
∴b=2.
故答案为:2;
(3)如图所示;
(4)由函数图象可知,函数的最小值为0.
故答案为:函数的最小值为0(答案不唯一).
【点睛】
本题考查的是一次函数的性质,根据题意画出函数图象,利用数形结合求解是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
