24.2 点和圆、直线和圆的位置关系 同步练习 上学期福建省部分地区九年级数学(含解析)
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系 同步练习 上学期福建省部分地区九年级数学(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览


文档简介
24.2 点和圆、直线和圆的位置关系
一、单选题
1.(2022秋·福建莆田·九年级统考期末)⊙O的半径为5,点P到圆心O的距离为5,点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O外 C.点P在⊙O上 D.无法确定
2.(2022秋·福建福州·九年级期末)平面内,的半径为,点到的距离为,过点可作的切线条数为( )
A.条 B.条 C.条 D.无数条
3.(2022秋·福建龙岩·九年级统考期末)若A,B,C是⊙上三点,,则⊙的半径是( )
A. B. C.6 D.
4.(2022秋·福建泉州·九年级期末)如图,为直径,,、为圆上两个动点,为中点,于,当、在圆上运动时保持,则的长( )
A.随、的运动位置而变化,且最大值为4
B.随、的运动位置而变化,且最小值为2
C.随、的运动位置长度保持不变,等于2
D.随、的运动位置而变化,没有最值
5.(2022秋·福建莆田·九年级统考期末)如图,AB、AC、BD是⊙O的切线,切点分别是P、C、D.若AB=5,AC=3,则BD的长是( )
A.4 B.3 C.2 D.1
二、填空题
6.(2022秋·福建莆田·九年级统考期末)如图,矩形ABCD中,AD=6,AB=8,AB是⊙O的直径.将矩形ABCD绕点A顺时针旋转得到矩形,且交⊙O于点E,交⊙O于点F,与⊙O相切于点M.下列说法正确的有 .(只填写序号)①AE=4;②;③;④.
7.(2022秋·福建福州·九年级统考期末)《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步.”该问题的答案是 步.
三、解答题
8.(2022秋·福建莆田·九年级期末)如图,在中,.
(1)请作出经过A、B两点的圆,且该圆的圆心O落在线段AC上(尺规作图,保留作图痕迹,不写做法);
(2)在(1)的条件下,已知,将线段AB绕点A逆时针旋转后与⊙O交于点E.试证明:B、C、E三点共线.
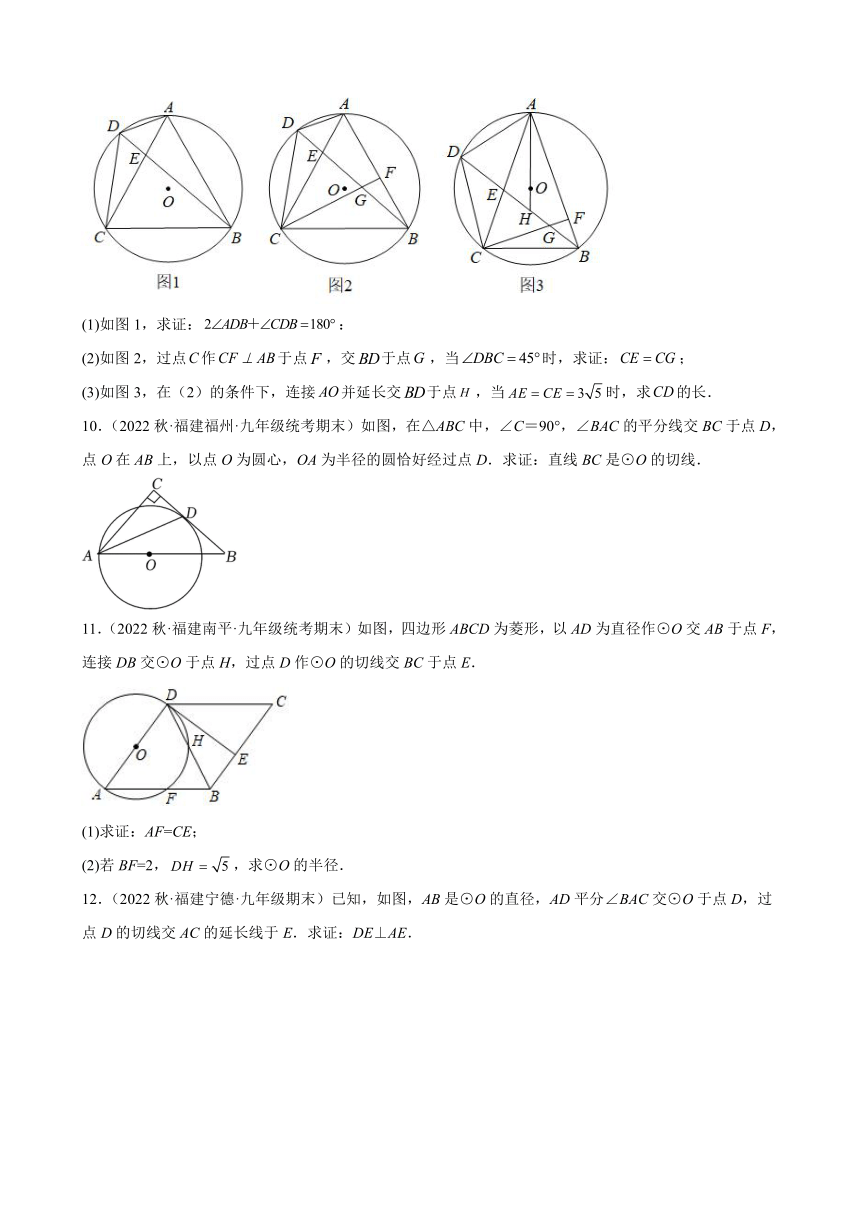
9.(2022秋·福建泉州·九年级期末)已知:四边形为的内接四边形,、相交于点,.
(1)如图1,求证::
(2)如图2,过点作于点,交于点,当时,求证:;
(3)如图3,在(2)的条件下,连接并延长交于点,当时,求的长.
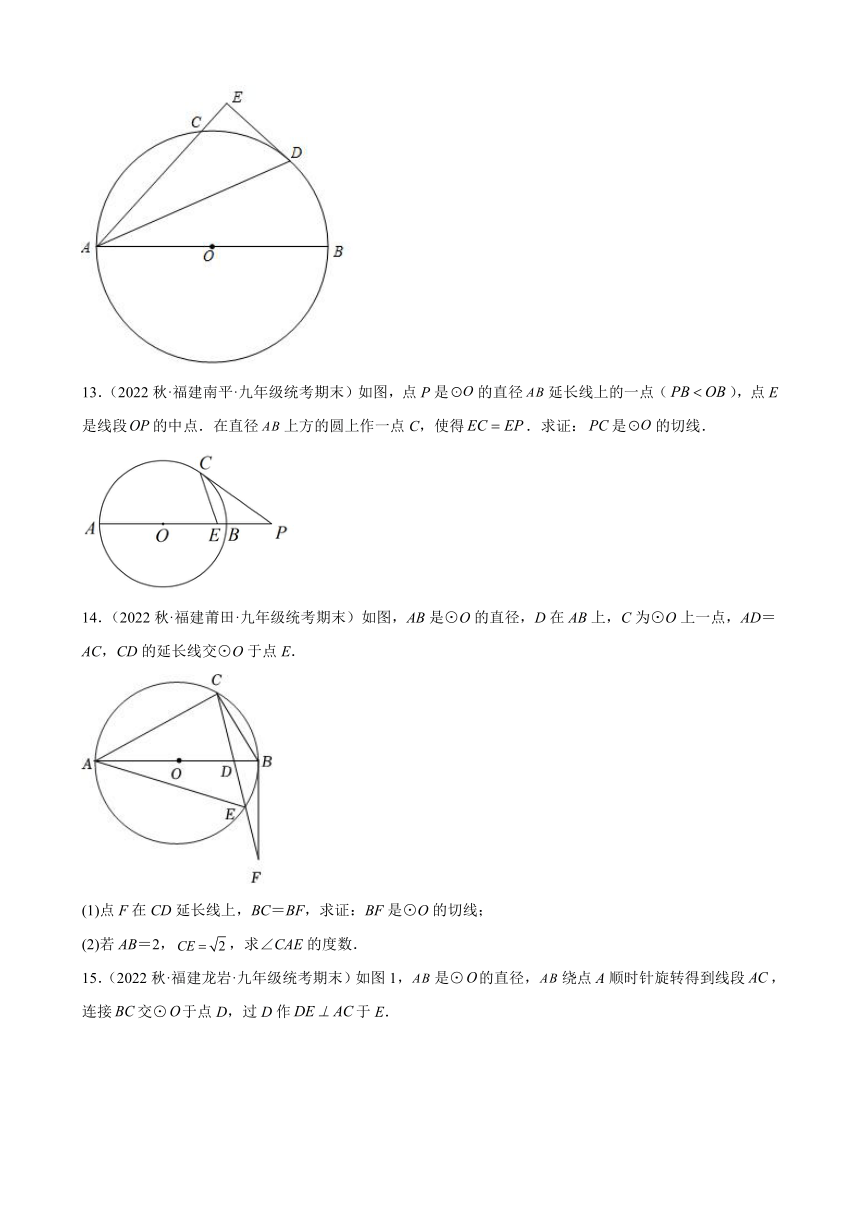
10.(2022秋·福建福州·九年级统考期末)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D.求证:直线BC是⊙O的切线.
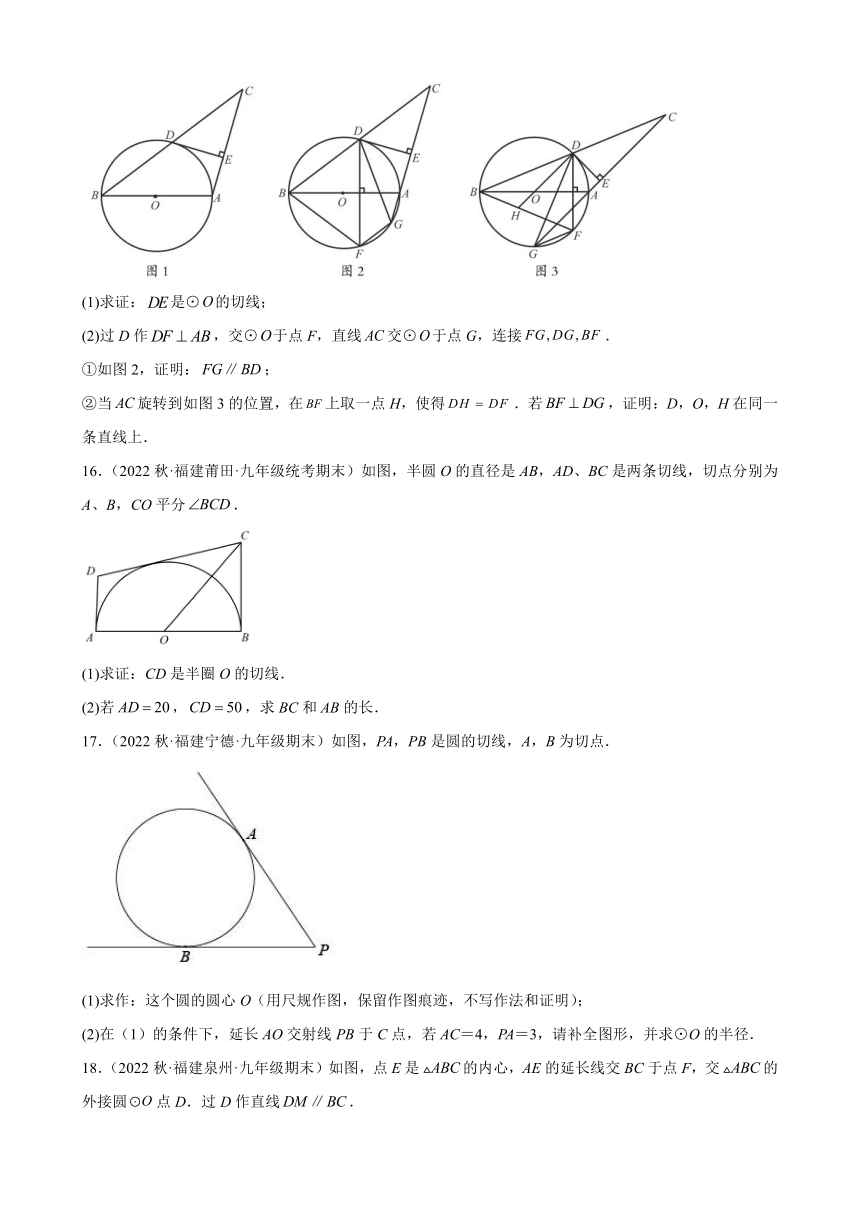
11.(2022秋·福建南平·九年级统考期末)如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,过点D作⊙O的切线交BC于点E.
(1)求证:AF=CE;
(2)若BF=2,,求⊙O的半径.
12.(2022秋·福建宁德·九年级期末)已知,如图,AB是⊙O的直径,AD平分∠BAC交⊙O于点D,过点D的切线交AC的延长线于E.求证:DE⊥AE.
13.(2022秋·福建南平·九年级统考期末)如图,点P是的直径延长线上的一点(),点E是线段的中点.在直径上方的圆上作一点C,使得.求证:是的切线.
14.(2022秋·福建莆田·九年级统考期末)如图,AB是⊙O的直径,D在AB上,C为⊙O上一点,AD=AC,CD的延长线交⊙O于点E.
(1)点F在CD延长线上,BC=BF,求证:BF是⊙O的切线;
(2)若AB=2,,求∠CAE的度数.
15.(2022秋·福建龙岩·九年级统考期末)如图1,是⊙的直径,绕点A顺时针旋转得到线段,连接交⊙于点D,过D作于E.
(1)求证:是⊙的切线;
(2)过D作,交⊙于点F,直线交⊙于点G,连接.
①如图2,证明:;
②当旋转到如图3的位置,在上取一点H,使得.若,证明:D,O,H在同一条直线上.
16.(2022秋·福建莆田·九年级统考期末)如图,半圆O的直径是AB,AD、BC是两条切线,切点分别为A、B,CO平分.
(1)求证:CD是半圈O的切线.
(2)若,,求BC和AB的长.
17.(2022秋·福建宁德·九年级期末)如图,PA,PB是圆的切线,A,B为切点.
(1)求作:这个圆的圆心O(用尺规作图,保留作图痕迹,不写作法和证明);
(2)在(1)的条件下,延长AO交射线PB于C点,若AC=4,PA=3,请补全图形,并求⊙O的半径.
18.(2022秋·福建泉州·九年级期末)如图,点E是的内心,AE的延长线交BC于点F,交的外接圆点D.过D作直线.
(1)求证:DM是的切线;
(2)求证:;
(3)若,,求的半径.
19.(2022秋·福建福州·九年级期末)如图,AB为的直径,点C在上,连接AC,BC,过点O作于点D,过点C作的切线交OD的延长线于点E.
(1)求证:;
(2)连接AD.若,,求AD的长.
20.(2022秋·福建莆田·九年级期末)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,过点C作CE⊥AD交AD的延长线于点E,延长EC,AB交于点F,∠ECD=∠BCF.
(1)求证:CE为⊙O的切线;
(2)若DE=1,CD=3,求⊙O的半径.
21.(2022秋·福建福州·九年级统考期末)如图,与等边的边,分别交于点,,是直径,过点作于点.
(1)求证:是的切线;
(2)连接,当是的切线时,求的半径与等边的边长之间的数量关系.
22.(2022秋·福建福州·九年级期末)如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=3.
(1)以BC边上一点O为圆心作⊙O,使⊙O分别与AC、AB都相切 (要求:尺规作图,保留作图痕迹,不写作法) ;
(2)求⊙O的面积.
23.(2022秋·福建厦门·九年级期末)如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
参考答案:
1.C
【分析】直接根据点与圆的位置关系的判定方法进行判断.
【详解】解:∵⊙O的半径为5,点P到圆心O的距离为5,
∴点P到圆心O的距离等于圆的半径,
∴点P在⊙O上.
故选:C.
【点睛】本题考查了点与圆的位置关系:点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外 d>r;点P在圆上 d=r;点P在圆内 d<r.
2.C
【分析】先确定点与圆的位置关系,再根据切线的定义即可直接得出答案.
【详解】解:的半径为,点到圆心的距离为,
,
点与的位置关系是:在外,
过圆外一点可以作圆的条切线,
故选:C.
【点睛】本题主要考查了点与圆的位置关系,切线的定义,切线就是与圆有且只有个公共点的直线,理解定义是关键.
3.C
【分析】⊙O的优弧AC上取一点D,连接AD、CD,连接OA、OC,∠ADC=180° ∠ABC=30°,根据圆周角定理求得∠AOC=2∠ADC=60°,根据等边三角形的判定定理知△AOB是等边三角形,所以等边三角形的三条边相等,即可求解.
【详解】解:⊙O的优弧AC上取一点D,连接AD、CD,连接OA、OC,如图所示:
∵∠ABC=150°,
∴∠ADC=180° ∠ABC=30°,
∴∠AOC=2∠ADC=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴OA=OC=AC=6,
∴⊙O的半径是6.
故选:C.
【点睛】本题考查了圆周角定理和等边三角形的判定与性质.解答该题时,利用圆周角定理要注意圆心角与圆周角的定义,只有三个点都在圆上所组成的角才称之为圆周角.
4.C
【分析】连接OC、ON、OD,由垂径定理可知ON⊥CD,∠CON=∠DON,然后由∠ONC+∠CMO=180°,可证明O、N、C、M四点共圆,从而可得到∠NOC=∠NMC=30°,于是可证明△OCD为等边三角形,从而得到CD=2.
【详解】解;连接:OC、ON、OD.
∵N是CD的中点,
∴ON⊥CD,∠CON=∠DON.
又∵CM⊥AB,
∴∠ONC+∠CMO=180°.
∴O、N、C、M四点共圆.
∴∠NOC=∠NMC=30°.
∴∠COD=60°.
又∵OC=OD,
∴△OCD为等边三角形.
∴CD=
故选:C.
【点睛】本题主要考查的是轨迹问题,发现O、N、C、M四点共圆,从而证得△OCD为等边三角形是解题的关键.
5.C
【分析】由于AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
【详解】解:∵AC、AP为⊙O的切线,
∴AC=AP=3,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=5﹣3=2.
故选:C.
【点睛】本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
6.①②③④
【分析】连接OE,OM,过点O作ON⊥AD′于点N,可得四边形OMD′N是矩形,证明OM=ND′=4,根据OA=OE,ON⊥AD′,可得AN=EN=2,进而可以判断①正确;证明△OAE是等边三角形,可得∠EOM=60°,∠BOM=60°,进而可以判断②正确;连接BF,根据AB是⊙O的直径,可得∠AFB=90°,利用含30度角的直角三角形即可判断③正确;根据∠DAB=90°,∠D′AO=60°,即可判断④正确.
【详解】解:如图,连接OE,OM,过点O作ON⊥AD′于点N,
∵D′C'与⊙O相切于点M,
∴OM⊥C′D′,
∴四边形OMD′N是矩形,
∴OM=ND′,
∵AB=8,AB是⊙O的直径,
∴OM=ND′=4,
在矩形ABCD中,由旋转可知:AD′=AD=6,
∴AN=AD′-ND′=6-4=2,
∵OA=OE,ON⊥AD′,
∴AN=EN=2,
∴AE=4,故①正确;
∵AE=AO=OE=4,
∴△OAE是等边三角形,
∴∠AOE=∠OEA=60°,
∴∠OED′=120°,
∵∠D′=∠OMD′=90°,
∴∠EOM=60°,
∴∠BOM=60°,
∴,故②正确;
如图,连接BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵∠EAO=60°,∠D′AB′=90°,
∴∠BAF=30°,
∴BF=AB=4,
∴AF=,故③正确;
∵∠DAB=90°,∠D′AO=60°,
∠DAD′=30°,故④正确.
综上所述:正确的有①②③④.
故答案为:①②③④.
【点睛】本题主要考查了切线的性质,圆周角定理,垂径定理,矩形的判定与性质,旋转的性质,等边三角形的判定与性质,含30度角的直角三角形,解决本题的关键是得到△OAE是等边三角形.
7.6
【分析】根据勾股定理求出直角三角形的斜边,根据直角三角形的内切圆的半径的求法确定出内切圆半径,得到直径.
【详解】解:根据勾股定理得:斜边为=17,
设内切圆半径为r,由面积法
r= 3(步),即直径为6步,
故答案为:6.
【点睛】考点:三角形的内切圆与内心.
8.(1)见解析
(2)见解析
【分析】(1)只需要作AB的垂直平分线,其与AC的交点即为圆心O,由此作图即可;
(2)先由圆周角定理求出,再由旋转的性质求出,从而得到,证明△OBC≌△OEC得到∠OCE=∠OCB=90°,则∠OCB+∠OCE=180°,即可证明B、C、E三点共线.
【详解】(1)解:如图所示,圆O即为所求;
(2)解:如图所示,连接CE,OE,
∵,
∴,
由旋转的性质可知,
∴,
∴,
在△OBC和△OEC中,
,
∴△OBC≌△OEC(SAS),
∴∠OCE=∠OCB=90°,
∴∠OCB+∠OCE=180°,
∴B、C、E三点共线.
【点睛】本题主要考查了线段垂直平分线的尺规作图,画圆,圆周角定理,旋转的性质,全等三角形的性质与判定等等,熟知性格知识是解题的关键.
9.(1)见解析
(2)见解析
(3)
【分析】(1)根据圆周角定理,将转化为的内角和即可;
(2)过点作交于点,交于点,可得,利用圆周角定理可知:,从而可得,再利用直角三角形两锐角互余可得,便能得到,从而证明结论;
(3)连接,作于,延长交于,由(2)知:,在上取,则四边形为,利用等腰三角形性质、平行四边形性质及勾股定理可求得,,,,,由弦AC与BD相交于E,可得,列出比例式即可求解.
【详解】(1)如图1,∵,
∴,
又∵,
∴,,
∴
(2)证明:过点作交于点,交于点,
∵,
∴,
∴
又∵,
∴.
∴,
∴
∵于,另有对顶角存在,
即:
∴,
∴,
∴,
∴:
(3)如图3,连接,作于,延长交于,
∵,
∴,
∵,
∴,
∴平分,
∴;.
连接,,
∴,
∴,
由(2)知:,在上取,则四边形为矩形,
∴,,
∴,
又∵,
∴,则
∵,
∴,,
∴,,
在中,
∵,
则,
∴,
∵弦AC与BD相交于E,
∴,
∴,
∴.
【点睛】本题是圆的综合题,主要考查了圆的相关性质,平行四边形的判定与性质,等腰直角三角形判定与性质,相似三角形的判定与性质,勾股定理等知识,作辅助线构造全等三角形是解题的关键.
10.证明见解析
【分析】连接,则,根据角平分线的定义可得∠CAD=∠OAD,等量代换可得∠CAD=∠ODA,可得,进而可证明OD⊥BC,即可得证.
【详解】解:证明:如图,连接OD,
∵OA=OD,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴,
∴∠ODB=∠C,
∵∠C=90°,
∴∠ODB=90°,
即OD⊥BC,
∵OD过圆心O,
∴直线BC是⊙O的切线.
【点睛】本题考查了圆的切线的判定,熟练掌握圆的切线的相关知识是解题的关键.
11.(1)见解析
(2)
【分析】(1)连接DF,根据菱形的性质可得AD=CD,AD∥BC,∠A=∠C.再由切线的性质,可得∠CED=∠ADE=90°.可证得△DAF≌△DCE.即可求证;
(2)连接AH,DF,根据等腰三角形的性质可得.在Rt△ADF和Rt△BDF中,根据勾股定理,即可求解.
【详解】(1)证明:如图,连接DF,
∵四边形ABCD为菱形,
∴AD=CD,AD∥BC,∠A=∠C.
∵DE是⊙O的切线,
∴∠ADE=90°.
∵AD∥BC,
∴∠CED=∠ADE=90°.
∵AD是⊙O的直径,
∴∠DFA=90°.
∴∠AFD=∠CED=90°.
在△DAF和△DCE中,,
∴△DAF≌△DCE(AAS).
∴AF=CE.
(2)解:如图,连接AH,DF,
∵AD是⊙O的直径,
∴∠AHD=∠DFA=90°.
∵AD=AB,,
∴.
在Rt△ADF和Rt△BDF中,
由勾股定理,得DF2=AD2-AF2,DF2=BD2-BF2,
∴AD2-AF2=BD2-BF2.
∴AD2-(AD-BF)2=BD2-BF2.
∴.
∴AD=5.
∴⊙O的半径为.
【点睛】本题考查了圆的综合,涉及了圆周角定理,菱形的性质,切线的性质,三角形全等的性质和判定,勾股定理等知识,解答本题的关键是根据勾股定理列方程解决问题.
12.见解析
【分析】由切线的性质可知∠ODE=90°,证得OD∥AE即可解决问题.
【详解】证明:连接OD.
∵DE是⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠CAD=∠DAB,
∴∠CAD=∠ODA,
∴OD∥AE,
∴∠E+∠ODE=180°,
∴∠E=90°,
∴DE⊥AE.
【点睛】本题考查切线的性质,平行线的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
13.证明见解析
【分析】连接OC,根据线段中点的定义得到OE=EP,求得OE=EC=EP,得到∠COE=∠ECO,∠ECP=∠P,利用三角形内角和定理求出,根据切线的判定定理即可得到结论.
【详解】证明:连接,
∵点E是线段的中点,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵是的半径,
∴是的切线.
【点睛】本题考查了切线的判定,等边对等角,三角形内角和定理,熟练掌握切线的判定定理是解题的关键.
14.(1)见解析
(2)45°
【分析】(1)要证明BF是⊙O的切线,只要求出∠OBF=90°即可,先根据直径所对的圆周角是直角,求出∠ACB=90°,再利用等边对等角得出∠ACD=∠ADC,∠BCD=∠F,即可解答;
(2)根据直径的长可得出半径的长,所以连接OC,OE,然后利用勾股定理的逆定理证明△COE是直角三角形,最后利用圆周角定理即可解答.
【详解】(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵AC=AD,
∴∠ACD=∠ADC,
∵∠ADC=∠BDF,
∴∠ACD=∠BDF,
∵BC=BF,
∴∠BCD=∠F,
∴∠BDF+∠F=90°,
∴∠FBD=180°-(∠FDB+∠F)=90°,
∵OB是圆O的半径,
∴BF是⊙O的切线;
(2)连接CO,EO,
∵AB=2,
∴OC=OE=1,
∵CE=,
∴CO2+EO2=2,CE2=()2=2,
∴CO2+EO2=CE2,
∴∠COE=90°,
∴∠CAE=∠COE=45°.
【点睛】本题考查了切线的判定与性质,圆周角定理,根据题目个已知条件并结合图形添加适当的辅助线是解题的关键.
15.(1)见解析
(2)①见解析;②见解析
【分析】(1)如图4,连接OD、AD,根据旋转可证得△ABC是等腰三角形,根据直径所对的圆周角是直角可得出AD⊥BC,根据三角形中位线性质可得ODAC,进而推出OD⊥DE,再运用切线的判定定理即可;
(2)①如图5,连接BG、AD,根据直径所对的圆周角是直角可得出AD⊥BC,再运用弦、弧、圆周角的关系即可证得结论;
②如图6,连接OD,运用圆周角定理及三角形内角和定理证明∠BDH=∠BDO,即可证得结论.
【详解】(1)证明:如图4,连接OD、AD,
∵AB绕点A顺时针旋转得到线段AC,
∴AB=AC,
∴△ABC是等腰三角形,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∴BD=CD且AO=BO,
∴OD是△ABC的中位线,
∴ODAC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)①证明:如图5,连接BG、AD,
∵AB是⊙O的直径,
∴∠BGA=∠BDA=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC,
∴BD=GD,
∴,
∵DF⊥AB,
∴,
∴,
∴∠1=∠2,
∴FGBD;
②证明:如图6,连接OD,
∵DF⊥AB,AB是⊙O的直径,
∴,
∴∠3=∠4=∠5,
∵AB=AC,
∴∠3=∠C,
∴∠5=∠C,
∴FGDB,
∴,
∴∠DBF=∠BDG,
∵BF⊥DG,
∴∠DBF=∠BDG=45°,,
∴∠3=∠4=∠DBF=22.5°,
∴∠7=90°﹣∠4=67.5°,
∵DF=DH,
∴∠6=∠7=67.5°,
∴∠BDH=∠6﹣∠DBF=22.5°,
∵OB=OD,
∴∠3=∠BDO=22.5°,
∴∠BDH=∠BDO,
∴D,O,H在同一条直线上.
【点睛】本题是圆的综合题,考查了切线的判定,等腰三角形的判定和性质,三角形中位线定理,圆周角定理,垂径定理,圆周角、弧、弦的关系等,熟练掌握圆周角、弧、弦的关系及圆的性质是解题关键.
16.(1)见解析
(2)
【分析】(1)过点O作OE⊥DC,垂足为E.由角平分线的性质定理得到OE=OB,从而可知DC是半圆O的切线;
(2)由切线长定理可知:DE=DA,EC=CB,从而可求得BC的长.
【详解】(1)证明:如图,过点O作于点E.
∵BC是半圆O的切线,
∴.
∵CO平分,
∴,
∴CD是半圆O的切线.
(2)解:∵AD,CD,BC是半圆O的切线,
∴,.
∵,
∴,
∴.
如图,过点D作于点F,故四边形DABF为矩形,
∴,,
∴.
在中,由勾股定理得,
∴.
【点睛】本题主要考查的是切线的性质和判定、切线长定理的应用,掌握切线的性质和判定、切线长定理是解题的关键.
17.(1)见解析;
(2)见解析,的半径为
【分析】(1)过点B作BP的垂线,作∠APB的平分线,二线的交点就是圆心;
(2)根据切线的性质,利用勾股定理,建立一元一次方程求解即可.
【详解】(1)如图所示,点O即为所求
(2)如图,∵PA是圆的切线,AO是半径,PB是圆的切线,
∴∠CAP=90°,PA=PB=3,∠CBO=90°,
∵AC=4,
∴PC==5,BC=5-3=2,
设圆的半径为x,则OC=4-x,
∴,
解得x=,
故圆的半径为.
【点睛】本题考查了垂线的画法,角的平分线的画法,切线的性质,切线长定理,勾股定理,一元一次方程的解法,熟练掌握切线的性质,切线长定理和勾股定理是解题的关键.
18.(1)见解析
(2)见解析
(3)⊙O的半径为5.
【分析】(1)连接OD交BC于H,根据圆周角定理和切线的判定即可证明;
(2)连接BD,由点E是△ABC的内心,得到∠ABE=∠CBE,∠DBC=∠BAD,推出∠BED=∠DBE,根据等角对等边得到BD=DE;
(3)根据垂径定理和勾股定理即可求出结果.
【详解】(1)证明:连接OD交BC于H,如图,
∵点E是△ABC的内心,
∴AD平分∠BAC,
即∠BAD=∠CAD,
∴,
∴OD⊥BC,BH=CH,
∵DM∥BC,
∴OD⊥DM,
∴DM是⊙O的切线;
(2)证明:∵点E是△ABC的内心,
∴∠ABE=∠CBE,
∵,
∴∠DBC=∠BAD,
∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE,
即∠BED=∠DBE,
∴BD=DE;
(3)解:设⊙O的半径为r,
连接OD,OB,如图,
由(1)得OD⊥BC,BH=CH,
∵BC=8,
∴BH=CH=4,
∵DE=2,BD=DE,
∴BD=2,
在Rt△BHD中,BD2=BH2+HD2,
∴(2)2=42+HD2,解得:HD=2,
在Rt△BHO中,
r2=BH2+(r-2)2,解得:r=5.
∴⊙O的半径为5.
【点睛】本题考查了三角形的内心,切线的判定与性质,三角形的外接圆与外心,圆周角定理,垂径定理,解决本题的关键是综合运用以上知识.
19.(1)证明见解析;(2)AD=4
【分析】(1)连接OC通过垂径定理和等腰三角形性质证明∠E=∠B
(2)连接AD通过计算发现BC=EC,再通过证明△CED≌△ABC得到AC=DC=4.
【详解】(1)证明:连接OC如图:
OD⊥CB
∴OB=OC,∠B=OCD
又CE为圆O的切线
∴OC⊥CE
∴∠ECD+∠DCO=∠ECD+∠E=90°
∴∠E=∠DCO=∠B
∴∠E=∠B
(2)连接AD如图
∵△EDC为Rt△
∴DE==8
由(1)得∠E=∠B
又AB为直径
∴∠BCA=90°
在△CED和△ABC中
∵
∴△CED≌△ABC(AAS)
∴AC=DC==4
∴
【点睛】本题考查垂径定理和全等三角形的判定与性质,掌握这些是本题解题关键.
20.(1)见解析;(2)⊙O的半径是4.5
【分析】(1)如图1,连接OC,先根据四边形ABCD内接于⊙O,得,再根据等量代换和直角三角形的性质可得,由切线的判定可得结论;
(2)如图2,过点O作于G,连接OC,OD,则,先根据三个角是直角的四边形是矩形得四边形OGEC是矩形,设⊙O的半径为x,根据勾股定理列方程可得结论.
【详解】(1)证明:如图1,连接OC,
∵,
∴,
∵四边形ABCD内接于⊙O,
∴
又
∴,
∵,
∴,
∵,
∴,
∴,
∵OC是⊙O的半径,
∴CE为⊙O的切线;
(2)解:如图2,过点O作于G,连接OC,OD,则,
∵,
∴四边形OGEC是矩形,
∴,
设⊙O的半径为x,
Rt△CDE中,,
∴,
∴,,
由勾股定理得,
∴,
解得:,
∴⊙O的半径是4.5.
【点睛】本题考查的是圆的综合,涉及到圆的切线的证明、勾股定理以及矩形的性质,熟练掌握相关性质是解决问题的关键.
21.(1)见详解;(2)
【分析】(1)连接OD,由题意易得∠A=∠B=60°,则有△AOD为等边三角形,进而可得OD∥BC,然后可得∠CFD=∠FDO=90°,最后问题可求证;
(2)连接DE,由(1)及题意易得,∠FDE=60°,则有△FDE是等边三角形,进而可得DE=DF,然后易得△CDF≌△AED,则有AE=CD=2r,最后问题可求解.
【详解】(1)证明:连接OD,如图所示:
∵等边,
∴∠A=∠B=60°,
∵,
∴△AOD为等边三角形,
∴,
∴OD∥BC,
∵,
∴∠CFD=∠FDO=90°,
∵OD是半径,
∴是的切线;
(2)解:连接DE,如图所示:
由(1)可得是的切线,∠FDO=90°,△AOD为等边三角形,
∴,
∴,
∵是的切线,
∴,
∴△FDE是等边三角形,
∴DE=DF,
∵,是直径,
∴,
∴△CDF≌△AED(AAS),
∴AE=CD=2r,
∴,
∵,
∴.
【点睛】本题主要考查切线的判定定理、切线长定理及等边三角形的判定与性质,熟练掌握切线的判定定理、切线长定理及等边三角形的判定与性质是解题的关键.
22.(1)图形见解析(2)3π
【分析】(1)直接利用角平分线的作法得出∠CAB的角平分线,进而得出答案;
(2)利用勾股定理得出⊙O的半径,进而利用圆的面积求法得出答案.
【详解】解:(1)如图所示:⊙O为所求的图形.
(2)在Rt△ABC中,
∵∠ABC=30°,
∴∠CAB=60°,
∵AO平分∠CAB,
∴∠CAO=30°,
设,则,
∵在Rt△ACO中,,
∴,
解得:或(负值不合题意,舍去),
∴⊙O的面积为.
【点睛】此题主要考查了复杂作图以及勾股定理,正确掌握角平分线的性质是解题关键.
23.(1)证明过程见解析;(2)12.
【分析】(1)连接OD,由BD为角平分线得到一对角相等,根据OB=OD,等边对等角得到一对角相等,等量代换得到一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直角,即可得证;
(2)过O作OG⊥BC,可得出四边形ODCG为矩形,在Rt△OBG中,利用勾股定理求出BG的长,由垂径定理可得BE=2BG.
【详解】(1)证明:连接OD,
∵BD为∠ABC的平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
∴AC为⊙O的切线;
(2)解:过O作OG⊥BC,连接OE,
∵∠C=∠ODC=90°,
∴∠C=∠ODC=∠OGC=90°,
∴四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
【点睛】此题考查了切线的判定,矩形的判定和性质,勾股定理以及垂径定理,熟练掌握切线的判定方法是解本题的关键.
一、单选题
1.(2022秋·福建莆田·九年级统考期末)⊙O的半径为5,点P到圆心O的距离为5,点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O外 C.点P在⊙O上 D.无法确定
2.(2022秋·福建福州·九年级期末)平面内,的半径为,点到的距离为,过点可作的切线条数为( )
A.条 B.条 C.条 D.无数条
3.(2022秋·福建龙岩·九年级统考期末)若A,B,C是⊙上三点,,则⊙的半径是( )
A. B. C.6 D.
4.(2022秋·福建泉州·九年级期末)如图,为直径,,、为圆上两个动点,为中点,于,当、在圆上运动时保持,则的长( )
A.随、的运动位置而变化,且最大值为4
B.随、的运动位置而变化,且最小值为2
C.随、的运动位置长度保持不变,等于2
D.随、的运动位置而变化,没有最值
5.(2022秋·福建莆田·九年级统考期末)如图,AB、AC、BD是⊙O的切线,切点分别是P、C、D.若AB=5,AC=3,则BD的长是( )
A.4 B.3 C.2 D.1
二、填空题
6.(2022秋·福建莆田·九年级统考期末)如图,矩形ABCD中,AD=6,AB=8,AB是⊙O的直径.将矩形ABCD绕点A顺时针旋转得到矩形,且交⊙O于点E,交⊙O于点F,与⊙O相切于点M.下列说法正确的有 .(只填写序号)①AE=4;②;③;④.
7.(2022秋·福建福州·九年级统考期末)《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步.”该问题的答案是 步.
三、解答题
8.(2022秋·福建莆田·九年级期末)如图,在中,.
(1)请作出经过A、B两点的圆,且该圆的圆心O落在线段AC上(尺规作图,保留作图痕迹,不写做法);
(2)在(1)的条件下,已知,将线段AB绕点A逆时针旋转后与⊙O交于点E.试证明:B、C、E三点共线.
9.(2022秋·福建泉州·九年级期末)已知:四边形为的内接四边形,、相交于点,.
(1)如图1,求证::
(2)如图2,过点作于点,交于点,当时,求证:;
(3)如图3,在(2)的条件下,连接并延长交于点,当时,求的长.
10.(2022秋·福建福州·九年级统考期末)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D.求证:直线BC是⊙O的切线.
11.(2022秋·福建南平·九年级统考期末)如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,过点D作⊙O的切线交BC于点E.
(1)求证:AF=CE;
(2)若BF=2,,求⊙O的半径.
12.(2022秋·福建宁德·九年级期末)已知,如图,AB是⊙O的直径,AD平分∠BAC交⊙O于点D,过点D的切线交AC的延长线于E.求证:DE⊥AE.
13.(2022秋·福建南平·九年级统考期末)如图,点P是的直径延长线上的一点(),点E是线段的中点.在直径上方的圆上作一点C,使得.求证:是的切线.
14.(2022秋·福建莆田·九年级统考期末)如图,AB是⊙O的直径,D在AB上,C为⊙O上一点,AD=AC,CD的延长线交⊙O于点E.
(1)点F在CD延长线上,BC=BF,求证:BF是⊙O的切线;
(2)若AB=2,,求∠CAE的度数.
15.(2022秋·福建龙岩·九年级统考期末)如图1,是⊙的直径,绕点A顺时针旋转得到线段,连接交⊙于点D,过D作于E.
(1)求证:是⊙的切线;
(2)过D作,交⊙于点F,直线交⊙于点G,连接.
①如图2,证明:;
②当旋转到如图3的位置,在上取一点H,使得.若,证明:D,O,H在同一条直线上.
16.(2022秋·福建莆田·九年级统考期末)如图,半圆O的直径是AB,AD、BC是两条切线,切点分别为A、B,CO平分.
(1)求证:CD是半圈O的切线.
(2)若,,求BC和AB的长.
17.(2022秋·福建宁德·九年级期末)如图,PA,PB是圆的切线,A,B为切点.
(1)求作:这个圆的圆心O(用尺规作图,保留作图痕迹,不写作法和证明);
(2)在(1)的条件下,延长AO交射线PB于C点,若AC=4,PA=3,请补全图形,并求⊙O的半径.
18.(2022秋·福建泉州·九年级期末)如图,点E是的内心,AE的延长线交BC于点F,交的外接圆点D.过D作直线.
(1)求证:DM是的切线;
(2)求证:;
(3)若,,求的半径.
19.(2022秋·福建福州·九年级期末)如图,AB为的直径,点C在上,连接AC,BC,过点O作于点D,过点C作的切线交OD的延长线于点E.
(1)求证:;
(2)连接AD.若,,求AD的长.
20.(2022秋·福建莆田·九年级期末)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,过点C作CE⊥AD交AD的延长线于点E,延长EC,AB交于点F,∠ECD=∠BCF.
(1)求证:CE为⊙O的切线;
(2)若DE=1,CD=3,求⊙O的半径.
21.(2022秋·福建福州·九年级统考期末)如图,与等边的边,分别交于点,,是直径,过点作于点.
(1)求证:是的切线;
(2)连接,当是的切线时,求的半径与等边的边长之间的数量关系.
22.(2022秋·福建福州·九年级期末)如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=3.
(1)以BC边上一点O为圆心作⊙O,使⊙O分别与AC、AB都相切 (要求:尺规作图,保留作图痕迹,不写作法) ;
(2)求⊙O的面积.
23.(2022秋·福建厦门·九年级期末)如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
参考答案:
1.C
【分析】直接根据点与圆的位置关系的判定方法进行判断.
【详解】解:∵⊙O的半径为5,点P到圆心O的距离为5,
∴点P到圆心O的距离等于圆的半径,
∴点P在⊙O上.
故选:C.
【点睛】本题考查了点与圆的位置关系:点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外 d>r;点P在圆上 d=r;点P在圆内 d<r.
2.C
【分析】先确定点与圆的位置关系,再根据切线的定义即可直接得出答案.
【详解】解:的半径为,点到圆心的距离为,
,
点与的位置关系是:在外,
过圆外一点可以作圆的条切线,
故选:C.
【点睛】本题主要考查了点与圆的位置关系,切线的定义,切线就是与圆有且只有个公共点的直线,理解定义是关键.
3.C
【分析】⊙O的优弧AC上取一点D,连接AD、CD,连接OA、OC,∠ADC=180° ∠ABC=30°,根据圆周角定理求得∠AOC=2∠ADC=60°,根据等边三角形的判定定理知△AOB是等边三角形,所以等边三角形的三条边相等,即可求解.
【详解】解:⊙O的优弧AC上取一点D,连接AD、CD,连接OA、OC,如图所示:
∵∠ABC=150°,
∴∠ADC=180° ∠ABC=30°,
∴∠AOC=2∠ADC=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴OA=OC=AC=6,
∴⊙O的半径是6.
故选:C.
【点睛】本题考查了圆周角定理和等边三角形的判定与性质.解答该题时,利用圆周角定理要注意圆心角与圆周角的定义,只有三个点都在圆上所组成的角才称之为圆周角.
4.C
【分析】连接OC、ON、OD,由垂径定理可知ON⊥CD,∠CON=∠DON,然后由∠ONC+∠CMO=180°,可证明O、N、C、M四点共圆,从而可得到∠NOC=∠NMC=30°,于是可证明△OCD为等边三角形,从而得到CD=2.
【详解】解;连接:OC、ON、OD.
∵N是CD的中点,
∴ON⊥CD,∠CON=∠DON.
又∵CM⊥AB,
∴∠ONC+∠CMO=180°.
∴O、N、C、M四点共圆.
∴∠NOC=∠NMC=30°.
∴∠COD=60°.
又∵OC=OD,
∴△OCD为等边三角形.
∴CD=
故选:C.
【点睛】本题主要考查的是轨迹问题,发现O、N、C、M四点共圆,从而证得△OCD为等边三角形是解题的关键.
5.C
【分析】由于AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
【详解】解:∵AC、AP为⊙O的切线,
∴AC=AP=3,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=5﹣3=2.
故选:C.
【点睛】本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
6.①②③④
【分析】连接OE,OM,过点O作ON⊥AD′于点N,可得四边形OMD′N是矩形,证明OM=ND′=4,根据OA=OE,ON⊥AD′,可得AN=EN=2,进而可以判断①正确;证明△OAE是等边三角形,可得∠EOM=60°,∠BOM=60°,进而可以判断②正确;连接BF,根据AB是⊙O的直径,可得∠AFB=90°,利用含30度角的直角三角形即可判断③正确;根据∠DAB=90°,∠D′AO=60°,即可判断④正确.
【详解】解:如图,连接OE,OM,过点O作ON⊥AD′于点N,
∵D′C'与⊙O相切于点M,
∴OM⊥C′D′,
∴四边形OMD′N是矩形,
∴OM=ND′,
∵AB=8,AB是⊙O的直径,
∴OM=ND′=4,
在矩形ABCD中,由旋转可知:AD′=AD=6,
∴AN=AD′-ND′=6-4=2,
∵OA=OE,ON⊥AD′,
∴AN=EN=2,
∴AE=4,故①正确;
∵AE=AO=OE=4,
∴△OAE是等边三角形,
∴∠AOE=∠OEA=60°,
∴∠OED′=120°,
∵∠D′=∠OMD′=90°,
∴∠EOM=60°,
∴∠BOM=60°,
∴,故②正确;
如图,连接BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵∠EAO=60°,∠D′AB′=90°,
∴∠BAF=30°,
∴BF=AB=4,
∴AF=,故③正确;
∵∠DAB=90°,∠D′AO=60°,
∠DAD′=30°,故④正确.
综上所述:正确的有①②③④.
故答案为:①②③④.
【点睛】本题主要考查了切线的性质,圆周角定理,垂径定理,矩形的判定与性质,旋转的性质,等边三角形的判定与性质,含30度角的直角三角形,解决本题的关键是得到△OAE是等边三角形.
7.6
【分析】根据勾股定理求出直角三角形的斜边,根据直角三角形的内切圆的半径的求法确定出内切圆半径,得到直径.
【详解】解:根据勾股定理得:斜边为=17,
设内切圆半径为r,由面积法
r= 3(步),即直径为6步,
故答案为:6.
【点睛】考点:三角形的内切圆与内心.
8.(1)见解析
(2)见解析
【分析】(1)只需要作AB的垂直平分线,其与AC的交点即为圆心O,由此作图即可;
(2)先由圆周角定理求出,再由旋转的性质求出,从而得到,证明△OBC≌△OEC得到∠OCE=∠OCB=90°,则∠OCB+∠OCE=180°,即可证明B、C、E三点共线.
【详解】(1)解:如图所示,圆O即为所求;
(2)解:如图所示,连接CE,OE,
∵,
∴,
由旋转的性质可知,
∴,
∴,
在△OBC和△OEC中,
,
∴△OBC≌△OEC(SAS),
∴∠OCE=∠OCB=90°,
∴∠OCB+∠OCE=180°,
∴B、C、E三点共线.
【点睛】本题主要考查了线段垂直平分线的尺规作图,画圆,圆周角定理,旋转的性质,全等三角形的性质与判定等等,熟知性格知识是解题的关键.
9.(1)见解析
(2)见解析
(3)
【分析】(1)根据圆周角定理,将转化为的内角和即可;
(2)过点作交于点,交于点,可得,利用圆周角定理可知:,从而可得,再利用直角三角形两锐角互余可得,便能得到,从而证明结论;
(3)连接,作于,延长交于,由(2)知:,在上取,则四边形为,利用等腰三角形性质、平行四边形性质及勾股定理可求得,,,,,由弦AC与BD相交于E,可得,列出比例式即可求解.
【详解】(1)如图1,∵,
∴,
又∵,
∴,,
∴
(2)证明:过点作交于点,交于点,
∵,
∴,
∴
又∵,
∴.
∴,
∴
∵于,另有对顶角存在,
即:
∴,
∴,
∴,
∴:
(3)如图3,连接,作于,延长交于,
∵,
∴,
∵,
∴,
∴平分,
∴;.
连接,,
∴,
∴,
由(2)知:,在上取,则四边形为矩形,
∴,,
∴,
又∵,
∴,则
∵,
∴,,
∴,,
在中,
∵,
则,
∴,
∵弦AC与BD相交于E,
∴,
∴,
∴.
【点睛】本题是圆的综合题,主要考查了圆的相关性质,平行四边形的判定与性质,等腰直角三角形判定与性质,相似三角形的判定与性质,勾股定理等知识,作辅助线构造全等三角形是解题的关键.
10.证明见解析
【分析】连接,则,根据角平分线的定义可得∠CAD=∠OAD,等量代换可得∠CAD=∠ODA,可得,进而可证明OD⊥BC,即可得证.
【详解】解:证明:如图,连接OD,
∵OA=OD,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴,
∴∠ODB=∠C,
∵∠C=90°,
∴∠ODB=90°,
即OD⊥BC,
∵OD过圆心O,
∴直线BC是⊙O的切线.
【点睛】本题考查了圆的切线的判定,熟练掌握圆的切线的相关知识是解题的关键.
11.(1)见解析
(2)
【分析】(1)连接DF,根据菱形的性质可得AD=CD,AD∥BC,∠A=∠C.再由切线的性质,可得∠CED=∠ADE=90°.可证得△DAF≌△DCE.即可求证;
(2)连接AH,DF,根据等腰三角形的性质可得.在Rt△ADF和Rt△BDF中,根据勾股定理,即可求解.
【详解】(1)证明:如图,连接DF,
∵四边形ABCD为菱形,
∴AD=CD,AD∥BC,∠A=∠C.
∵DE是⊙O的切线,
∴∠ADE=90°.
∵AD∥BC,
∴∠CED=∠ADE=90°.
∵AD是⊙O的直径,
∴∠DFA=90°.
∴∠AFD=∠CED=90°.
在△DAF和△DCE中,,
∴△DAF≌△DCE(AAS).
∴AF=CE.
(2)解:如图,连接AH,DF,
∵AD是⊙O的直径,
∴∠AHD=∠DFA=90°.
∵AD=AB,,
∴.
在Rt△ADF和Rt△BDF中,
由勾股定理,得DF2=AD2-AF2,DF2=BD2-BF2,
∴AD2-AF2=BD2-BF2.
∴AD2-(AD-BF)2=BD2-BF2.
∴.
∴AD=5.
∴⊙O的半径为.
【点睛】本题考查了圆的综合,涉及了圆周角定理,菱形的性质,切线的性质,三角形全等的性质和判定,勾股定理等知识,解答本题的关键是根据勾股定理列方程解决问题.
12.见解析
【分析】由切线的性质可知∠ODE=90°,证得OD∥AE即可解决问题.
【详解】证明:连接OD.
∵DE是⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠CAD=∠DAB,
∴∠CAD=∠ODA,
∴OD∥AE,
∴∠E+∠ODE=180°,
∴∠E=90°,
∴DE⊥AE.
【点睛】本题考查切线的性质,平行线的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
13.证明见解析
【分析】连接OC,根据线段中点的定义得到OE=EP,求得OE=EC=EP,得到∠COE=∠ECO,∠ECP=∠P,利用三角形内角和定理求出,根据切线的判定定理即可得到结论.
【详解】证明:连接,
∵点E是线段的中点,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵是的半径,
∴是的切线.
【点睛】本题考查了切线的判定,等边对等角,三角形内角和定理,熟练掌握切线的判定定理是解题的关键.
14.(1)见解析
(2)45°
【分析】(1)要证明BF是⊙O的切线,只要求出∠OBF=90°即可,先根据直径所对的圆周角是直角,求出∠ACB=90°,再利用等边对等角得出∠ACD=∠ADC,∠BCD=∠F,即可解答;
(2)根据直径的长可得出半径的长,所以连接OC,OE,然后利用勾股定理的逆定理证明△COE是直角三角形,最后利用圆周角定理即可解答.
【详解】(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵AC=AD,
∴∠ACD=∠ADC,
∵∠ADC=∠BDF,
∴∠ACD=∠BDF,
∵BC=BF,
∴∠BCD=∠F,
∴∠BDF+∠F=90°,
∴∠FBD=180°-(∠FDB+∠F)=90°,
∵OB是圆O的半径,
∴BF是⊙O的切线;
(2)连接CO,EO,
∵AB=2,
∴OC=OE=1,
∵CE=,
∴CO2+EO2=2,CE2=()2=2,
∴CO2+EO2=CE2,
∴∠COE=90°,
∴∠CAE=∠COE=45°.
【点睛】本题考查了切线的判定与性质,圆周角定理,根据题目个已知条件并结合图形添加适当的辅助线是解题的关键.
15.(1)见解析
(2)①见解析;②见解析
【分析】(1)如图4,连接OD、AD,根据旋转可证得△ABC是等腰三角形,根据直径所对的圆周角是直角可得出AD⊥BC,根据三角形中位线性质可得ODAC,进而推出OD⊥DE,再运用切线的判定定理即可;
(2)①如图5,连接BG、AD,根据直径所对的圆周角是直角可得出AD⊥BC,再运用弦、弧、圆周角的关系即可证得结论;
②如图6,连接OD,运用圆周角定理及三角形内角和定理证明∠BDH=∠BDO,即可证得结论.
【详解】(1)证明:如图4,连接OD、AD,
∵AB绕点A顺时针旋转得到线段AC,
∴AB=AC,
∴△ABC是等腰三角形,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∴BD=CD且AO=BO,
∴OD是△ABC的中位线,
∴ODAC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)①证明:如图5,连接BG、AD,
∵AB是⊙O的直径,
∴∠BGA=∠BDA=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC,
∴BD=GD,
∴,
∵DF⊥AB,
∴,
∴,
∴∠1=∠2,
∴FGBD;
②证明:如图6,连接OD,
∵DF⊥AB,AB是⊙O的直径,
∴,
∴∠3=∠4=∠5,
∵AB=AC,
∴∠3=∠C,
∴∠5=∠C,
∴FGDB,
∴,
∴∠DBF=∠BDG,
∵BF⊥DG,
∴∠DBF=∠BDG=45°,,
∴∠3=∠4=∠DBF=22.5°,
∴∠7=90°﹣∠4=67.5°,
∵DF=DH,
∴∠6=∠7=67.5°,
∴∠BDH=∠6﹣∠DBF=22.5°,
∵OB=OD,
∴∠3=∠BDO=22.5°,
∴∠BDH=∠BDO,
∴D,O,H在同一条直线上.
【点睛】本题是圆的综合题,考查了切线的判定,等腰三角形的判定和性质,三角形中位线定理,圆周角定理,垂径定理,圆周角、弧、弦的关系等,熟练掌握圆周角、弧、弦的关系及圆的性质是解题关键.
16.(1)见解析
(2)
【分析】(1)过点O作OE⊥DC,垂足为E.由角平分线的性质定理得到OE=OB,从而可知DC是半圆O的切线;
(2)由切线长定理可知:DE=DA,EC=CB,从而可求得BC的长.
【详解】(1)证明:如图,过点O作于点E.
∵BC是半圆O的切线,
∴.
∵CO平分,
∴,
∴CD是半圆O的切线.
(2)解:∵AD,CD,BC是半圆O的切线,
∴,.
∵,
∴,
∴.
如图,过点D作于点F,故四边形DABF为矩形,
∴,,
∴.
在中,由勾股定理得,
∴.
【点睛】本题主要考查的是切线的性质和判定、切线长定理的应用,掌握切线的性质和判定、切线长定理是解题的关键.
17.(1)见解析;
(2)见解析,的半径为
【分析】(1)过点B作BP的垂线,作∠APB的平分线,二线的交点就是圆心;
(2)根据切线的性质,利用勾股定理,建立一元一次方程求解即可.
【详解】(1)如图所示,点O即为所求
(2)如图,∵PA是圆的切线,AO是半径,PB是圆的切线,
∴∠CAP=90°,PA=PB=3,∠CBO=90°,
∵AC=4,
∴PC==5,BC=5-3=2,
设圆的半径为x,则OC=4-x,
∴,
解得x=,
故圆的半径为.
【点睛】本题考查了垂线的画法,角的平分线的画法,切线的性质,切线长定理,勾股定理,一元一次方程的解法,熟练掌握切线的性质,切线长定理和勾股定理是解题的关键.
18.(1)见解析
(2)见解析
(3)⊙O的半径为5.
【分析】(1)连接OD交BC于H,根据圆周角定理和切线的判定即可证明;
(2)连接BD,由点E是△ABC的内心,得到∠ABE=∠CBE,∠DBC=∠BAD,推出∠BED=∠DBE,根据等角对等边得到BD=DE;
(3)根据垂径定理和勾股定理即可求出结果.
【详解】(1)证明:连接OD交BC于H,如图,
∵点E是△ABC的内心,
∴AD平分∠BAC,
即∠BAD=∠CAD,
∴,
∴OD⊥BC,BH=CH,
∵DM∥BC,
∴OD⊥DM,
∴DM是⊙O的切线;
(2)证明:∵点E是△ABC的内心,
∴∠ABE=∠CBE,
∵,
∴∠DBC=∠BAD,
∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE,
即∠BED=∠DBE,
∴BD=DE;
(3)解:设⊙O的半径为r,
连接OD,OB,如图,
由(1)得OD⊥BC,BH=CH,
∵BC=8,
∴BH=CH=4,
∵DE=2,BD=DE,
∴BD=2,
在Rt△BHD中,BD2=BH2+HD2,
∴(2)2=42+HD2,解得:HD=2,
在Rt△BHO中,
r2=BH2+(r-2)2,解得:r=5.
∴⊙O的半径为5.
【点睛】本题考查了三角形的内心,切线的判定与性质,三角形的外接圆与外心,圆周角定理,垂径定理,解决本题的关键是综合运用以上知识.
19.(1)证明见解析;(2)AD=4
【分析】(1)连接OC通过垂径定理和等腰三角形性质证明∠E=∠B
(2)连接AD通过计算发现BC=EC,再通过证明△CED≌△ABC得到AC=DC=4.
【详解】(1)证明:连接OC如图:
OD⊥CB
∴OB=OC,∠B=OCD
又CE为圆O的切线
∴OC⊥CE
∴∠ECD+∠DCO=∠ECD+∠E=90°
∴∠E=∠DCO=∠B
∴∠E=∠B
(2)连接AD如图
∵△EDC为Rt△
∴DE==8
由(1)得∠E=∠B
又AB为直径
∴∠BCA=90°
在△CED和△ABC中
∵
∴△CED≌△ABC(AAS)
∴AC=DC==4
∴
【点睛】本题考查垂径定理和全等三角形的判定与性质,掌握这些是本题解题关键.
20.(1)见解析;(2)⊙O的半径是4.5
【分析】(1)如图1,连接OC,先根据四边形ABCD内接于⊙O,得,再根据等量代换和直角三角形的性质可得,由切线的判定可得结论;
(2)如图2,过点O作于G,连接OC,OD,则,先根据三个角是直角的四边形是矩形得四边形OGEC是矩形,设⊙O的半径为x,根据勾股定理列方程可得结论.
【详解】(1)证明:如图1,连接OC,
∵,
∴,
∵四边形ABCD内接于⊙O,
∴
又
∴,
∵,
∴,
∵,
∴,
∴,
∵OC是⊙O的半径,
∴CE为⊙O的切线;
(2)解:如图2,过点O作于G,连接OC,OD,则,
∵,
∴四边形OGEC是矩形,
∴,
设⊙O的半径为x,
Rt△CDE中,,
∴,
∴,,
由勾股定理得,
∴,
解得:,
∴⊙O的半径是4.5.
【点睛】本题考查的是圆的综合,涉及到圆的切线的证明、勾股定理以及矩形的性质,熟练掌握相关性质是解决问题的关键.
21.(1)见详解;(2)
【分析】(1)连接OD,由题意易得∠A=∠B=60°,则有△AOD为等边三角形,进而可得OD∥BC,然后可得∠CFD=∠FDO=90°,最后问题可求证;
(2)连接DE,由(1)及题意易得,∠FDE=60°,则有△FDE是等边三角形,进而可得DE=DF,然后易得△CDF≌△AED,则有AE=CD=2r,最后问题可求解.
【详解】(1)证明:连接OD,如图所示:
∵等边,
∴∠A=∠B=60°,
∵,
∴△AOD为等边三角形,
∴,
∴OD∥BC,
∵,
∴∠CFD=∠FDO=90°,
∵OD是半径,
∴是的切线;
(2)解:连接DE,如图所示:
由(1)可得是的切线,∠FDO=90°,△AOD为等边三角形,
∴,
∴,
∵是的切线,
∴,
∴△FDE是等边三角形,
∴DE=DF,
∵,是直径,
∴,
∴△CDF≌△AED(AAS),
∴AE=CD=2r,
∴,
∵,
∴.
【点睛】本题主要考查切线的判定定理、切线长定理及等边三角形的判定与性质,熟练掌握切线的判定定理、切线长定理及等边三角形的判定与性质是解题的关键.
22.(1)图形见解析(2)3π
【分析】(1)直接利用角平分线的作法得出∠CAB的角平分线,进而得出答案;
(2)利用勾股定理得出⊙O的半径,进而利用圆的面积求法得出答案.
【详解】解:(1)如图所示:⊙O为所求的图形.
(2)在Rt△ABC中,
∵∠ABC=30°,
∴∠CAB=60°,
∵AO平分∠CAB,
∴∠CAO=30°,
设,则,
∵在Rt△ACO中,,
∴,
解得:或(负值不合题意,舍去),
∴⊙O的面积为.
【点睛】此题主要考查了复杂作图以及勾股定理,正确掌握角平分线的性质是解题关键.
23.(1)证明过程见解析;(2)12.
【分析】(1)连接OD,由BD为角平分线得到一对角相等,根据OB=OD,等边对等角得到一对角相等,等量代换得到一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直角,即可得证;
(2)过O作OG⊥BC,可得出四边形ODCG为矩形,在Rt△OBG中,利用勾股定理求出BG的长,由垂径定理可得BE=2BG.
【详解】(1)证明:连接OD,
∵BD为∠ABC的平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
∴AC为⊙O的切线;
(2)解:过O作OG⊥BC,连接OE,
∵∠C=∠ODC=90°,
∴∠C=∠ODC=∠OGC=90°,
∴四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
【点睛】此题考查了切线的判定,矩形的判定和性质,勾股定理以及垂径定理,熟练掌握切线的判定方法是解本题的关键.
同课章节目录
