数学人教A版(2019)必修第一册1.2集合间的基本关系课件(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册1.2集合间的基本关系课件(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 46.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
第一章 集合与常用逻辑用语
1.2 集合间的基本关系
目录
01
子集
02
相等
03
真子集
子集
01
一、新旧知识的联系
情景1-实数的大小关系:
我们知道,两个实数之间有相等关系,大小关系。比如:5=5,5>3,1<5。那么集合之间是否也有类似的关系呢?
二、实际问题
情景2-教师队伍:
集合A={x| x是我校女教师},集合B={x|x是我校教师}
请问:集合A和集合B有什么关系?
情景3-我班学生:
集合C为我班的男学生,集合D为我班全体学生。
请问:集合C和集合D有什么关系?
集合C中的元素都是集合D中的元素。
集合A中的元素都是集合B中的元素。
集合A中的元素个数<集合B中的元素个数
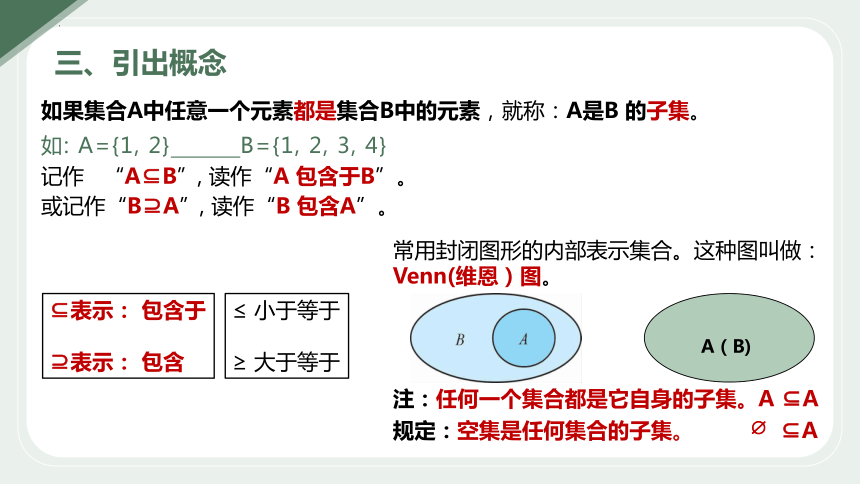
三、引出概念
如果集合A中任意一个元素都是集合B中的元素,就称:A是B 的子集。
记作 “A B”, 读作“A 包含于B”。
或记作“B A”, 读作“B 包含A”。
表示: 包含于
表示: 包含
常用封闭图形的内部表示集合。这种图叫做:
Venn(维恩)图。
A(B)
注:任何一个集合都是它自身的子集。A A
规定:空集是任何集合的子集。 A
如: A={1, 2} B={1, 2, 3, 4}
≤ 小于等于
≥ 大于等于
四、空集
不含任何元素的集合,叫做空集。记作: 。
= { }
易错:
0
{0}
{0}
{x|x =-1}
或
五、例题讲解
例题1:用适当的符号填空
“∈”,“ ”,“ ”,“ ”,“ ”,“ ”
(1) 0 (2) 3 {1, 2, 3, 4}
(3) A={x | x是三角形} B={x | x是矩形}
(4) {1,3,5} {1, 3, 5, 7} {1, 3, 5, 7, 9}
(5) {1,3,5} {1, 3, 5, 7, 9}
∈
结论:若A B,且B C。则A C。
C
B
A
六、课堂练习
当子集只含有3个元素:
∴ {a, b, c}是集合A的子集
综上所述:
集合{a,b,c}的所有子集有:
,{a}, {b}, {c},
{a, b}, {a, c}, {b, c},
{a, b, c}
课堂练 ---P8
1. 写出集合{a,b,c}的所有子集。
1. 解析:设集合A={a, b, c}
∵ 空集是任何集合的子集
∴ 是集合A的子集;
当子集只含有1个元素:
∴ {a}, {b}, {c}是集合A的子集
当子集只含有2个元素:
∴ {a, b}, {a, c}, {b, c}是集合A的子集
六、课堂练习
课堂练 ---P8
2. 用适当的符号填空:
(1) a {a, b, c}
(2) 0 {x | x =0}
(3) {x∈R | x +1=0}
(4) {0, 1} N
∈
(2) 解析:
∵ {x | x =0}是集合。即集合{x | x=0}
∵ 0是元素
∴ 0 ∈ {x | x =0}
∈
(3) 解析:
∵ {x∈R | x +1=0},中x +1=0无解
∴ {x∈R | x +1=0}是
∴ {x∈R | x +1=0}
或 = {x∈R | x +1=0}
或 =
(1) 解析:
∵ a是元素,{a, b, c}是集合。
∵ 元素a是集合{a, b, c}中的元素。
∴ a ∈ {a, b, c}
(4) 解析:
∵ {0, 1}是集合
自然数集N={0, 1, 2, 3, 4...}
∵ {0, 1}中的元素都是集合N中的元素
∴ {0, 1} N
六、课堂练习
课堂练 ---P9
2. 用适当的符号填空:
(5) {0} {x | x =x}
(6) {2, 1} {x | x -3x+2=0}
(6) 解析:
∵ {x | x -3x+2=0}
∵ x -3x+2=0
∴ (x-1)(x-2)=0
∴ 解得:x=1或x=2
∴ {2, 1} ={x | x=1或x=2}
或 =
(5) 解析:
∵ {x | x =x}中
∵ x =x
∴ 解得:x=0或x=1
∴ {x | x=0或x=1}
∴ {0} {x | x=0或x=1}
相等
02
一、引出概念
若集合A中的元素都是集合B中的元素,集合B中的元素都是集合A中的元素。
那么集合A=集合B
Venn(维恩)图
A(B)
A=B
实数的大小关系:
“若a≤b,且b≥a,则a=b”
若A B,且B A,则A=B
二、课堂练习
课堂练
1. 用适当的符号填空
(1) {3, 2, 1} {1, 2, 3} (2) N* Z+
(3) A={x | x是正方形或长方形} B={x | x是矩形}
(4) {0, 1, -1} {x| x =x4}
=
=
=
=
真子集
03
一、引出概念
如果集合A是集合B的子集,并且集合B中至少有一个元素不属于集合A。
则A是B 的真子集。
记作A B (或B A),读作“A 真包含于B”或 “B真包含A”
如: A={1, 2} B={1, 2, 3, 4}
A B A 真包含于B
B A B 真包含A
Venn(维恩)图
注:空集是任何非空集合的真子集。
即,对任何非空集合A, 总有 A
< 小于
> 大于
二、例题讲解
例题1:用适当的符号填空
“ ”,“ ”
(4) {1,3,5} {1, 3, 5, 7} {1, 3, 5, 7, 9}
(5) {1,3,5} {1, 3, 5, 7, 9}
三、课堂练习
1. 解析:
∵ 集合{a,b,c}的所有子集有:
,{a}, {b}, {c}, {a, b}, {a, c}, {b, c},{a, b, c}
∴ 集合{a,b,c}的所有真子集有:
,{a}, {b}, {c}, {a, b}, {a, c}, {b, c}
课堂练
1. 写出集合{a,b,c}的所有子集,指出哪些是它的真子集。
三、课堂练习
课堂练
3.判断下列两个集合之间的关系 ---P9
(1)A={x | x<0}, B={x | x<1}
(2)A={x | x=3k, k∈Z}, B={x | x=6z, z∈N}
(3) A={x∈N+| x是4与10的公倍数}, B={x | x=20m,m∈N+}
三、课堂练习
课堂练
3.判断下列两个集合之间的关系 ---P9
(1)A={x | x<0}, B={x | x<1}
(1) 解析:
A
B
如图:
集合A中的元素都是集合B中的元素,且集合B中至少有一个元素不属于集合A。则A是B的真子集。
A B
三、课堂练习
课堂练
3.判断下列两个集合之间的关系 ---P9
(2)A={x | x=3k, k∈Z}, B={x | x=6z, z∈N}
(2) 解析:
集合A:
∵k∈Z, 令k=...-2,-1,0,1,2,3,4,5,6...
∴x=...-6,-3,0,3,6,9,12,15,18...
∴A={x | x=..-6,-3,0,3,6,9,12,15,18...}
集合B:
∵z∈N,令z=0, 1, 2, 3...
∴x=0, 6, 12, 18...
∴B={x | x=0, 6, 12, 18...}
∴ B是A的真子集。B A,或者A B
三、课堂练习
课堂练
3.判断下列两个集合之间的关系 ---P9
(3) A={x∈N+| x是4与10的公倍数}, B={x | x=20m,m∈N+}
解析:
集合A:
∵ x是4与10的公倍数
∴ x=20, 40,60, 80...
∴ A={x | x=20, 40,60, 80...}
集合B:
∵ m为非0自然数
∴ 令m=1, 2, 3, 4...
∴ B={x | x=20, 40,60, 80...}
∴ A =B
课堂小结
04
课堂小结
集合间的基本关系:子集,相等,真子集
集合与元素的关系:属于“ ∈ ”,不属于“ ”
集合与集合的关系:
子集: “ ” 包含于, “ ” 包含
相等关系: “ = ” 相等
真子集: “ ”真包含于, “ ”真包含
课后作业
05
课后作业
1、判断题
(1)0∈ ( )
(2)0= ( )
(3) {9, 10, 7, 2} ( )
(4){x|x -1=0}与{1}相等 ( )
(5){(0,0)} {(x,y)|x-y=0 ( )
课后作业
2、用适当的符号填空题:
(1) A={x| x+5<10}, B={x| x +1=5}。集合A 集合B
(2)若集合A={x|x -9=0},B={3},C={3,-3}
3 A,B A,C A
3、用Venn图表示下列集合的关系:
A={x|x是正方形},B={x|x是梯形},C={x|x是平行四边形},
D={x|x是矩形},E={x|x是菱形}
课后作业
4、解答题
(1)A={1,2,3},请分别写出集合A所有的子集,真子集。
A的子集个数是多少?非空子集个数是多少?
真子集个数是多少?非空真子集个数是多少?
(2)A={1,2,3,4},请分别写出集合A所有的子集,真子集。
A的子集个数是多少?非空子集个数是多少?
真子集个数是多少?非空真子集个数是多少?
(3)如果A中有a个元素,那么:
A的子集个数是多少?非空子集个数是多少?
真子集个数是多少?非空真子集个数是多少?
课后作业
5、解答题
(1)设m,n∈Z, 若P={1,-m}, W={m, n},P=W。
求m-2n的值
(2)已知集合A={x| -4且B是A的真子集。求m的范围
低头是题海
抬头是未来
THANKS
第一章 集合与常用逻辑用语
1.2 集合间的基本关系
目录
01
子集
02
相等
03
真子集
子集
01
一、新旧知识的联系
情景1-实数的大小关系:
我们知道,两个实数之间有相等关系,大小关系。比如:5=5,5>3,1<5。那么集合之间是否也有类似的关系呢?
二、实际问题
情景2-教师队伍:
集合A={x| x是我校女教师},集合B={x|x是我校教师}
请问:集合A和集合B有什么关系?
情景3-我班学生:
集合C为我班的男学生,集合D为我班全体学生。
请问:集合C和集合D有什么关系?
集合C中的元素都是集合D中的元素。
集合A中的元素都是集合B中的元素。
集合A中的元素个数<集合B中的元素个数
三、引出概念
如果集合A中任意一个元素都是集合B中的元素,就称:A是B 的子集。
记作 “A B”, 读作“A 包含于B”。
或记作“B A”, 读作“B 包含A”。
表示: 包含于
表示: 包含
常用封闭图形的内部表示集合。这种图叫做:
Venn(维恩)图。
A(B)
注:任何一个集合都是它自身的子集。A A
规定:空集是任何集合的子集。 A
如: A={1, 2} B={1, 2, 3, 4}
≤ 小于等于
≥ 大于等于
四、空集
不含任何元素的集合,叫做空集。记作: 。
= { }
易错:
0
{0}
{0}
{x|x =-1}
或
五、例题讲解
例题1:用适当的符号填空
“∈”,“ ”,“ ”,“ ”,“ ”,“ ”
(1) 0 (2) 3 {1, 2, 3, 4}
(3) A={x | x是三角形} B={x | x是矩形}
(4) {1,3,5} {1, 3, 5, 7} {1, 3, 5, 7, 9}
(5) {1,3,5} {1, 3, 5, 7, 9}
∈
结论:若A B,且B C。则A C。
C
B
A
六、课堂练习
当子集只含有3个元素:
∴ {a, b, c}是集合A的子集
综上所述:
集合{a,b,c}的所有子集有:
,{a}, {b}, {c},
{a, b}, {a, c}, {b, c},
{a, b, c}
课堂练 ---P8
1. 写出集合{a,b,c}的所有子集。
1. 解析:设集合A={a, b, c}
∵ 空集是任何集合的子集
∴ 是集合A的子集;
当子集只含有1个元素:
∴ {a}, {b}, {c}是集合A的子集
当子集只含有2个元素:
∴ {a, b}, {a, c}, {b, c}是集合A的子集
六、课堂练习
课堂练 ---P8
2. 用适当的符号填空:
(1) a {a, b, c}
(2) 0 {x | x =0}
(3) {x∈R | x +1=0}
(4) {0, 1} N
∈
(2) 解析:
∵ {x | x =0}是集合。即集合{x | x=0}
∵ 0是元素
∴ 0 ∈ {x | x =0}
∈
(3) 解析:
∵ {x∈R | x +1=0},中x +1=0无解
∴ {x∈R | x +1=0}是
∴ {x∈R | x +1=0}
或 = {x∈R | x +1=0}
或 =
(1) 解析:
∵ a是元素,{a, b, c}是集合。
∵ 元素a是集合{a, b, c}中的元素。
∴ a ∈ {a, b, c}
(4) 解析:
∵ {0, 1}是集合
自然数集N={0, 1, 2, 3, 4...}
∵ {0, 1}中的元素都是集合N中的元素
∴ {0, 1} N
六、课堂练习
课堂练 ---P9
2. 用适当的符号填空:
(5) {0} {x | x =x}
(6) {2, 1} {x | x -3x+2=0}
(6) 解析:
∵ {x | x -3x+2=0}
∵ x -3x+2=0
∴ (x-1)(x-2)=0
∴ 解得:x=1或x=2
∴ {2, 1} ={x | x=1或x=2}
或 =
(5) 解析:
∵ {x | x =x}中
∵ x =x
∴ 解得:x=0或x=1
∴ {x | x=0或x=1}
∴ {0} {x | x=0或x=1}
相等
02
一、引出概念
若集合A中的元素都是集合B中的元素,集合B中的元素都是集合A中的元素。
那么集合A=集合B
Venn(维恩)图
A(B)
A=B
实数的大小关系:
“若a≤b,且b≥a,则a=b”
若A B,且B A,则A=B
二、课堂练习
课堂练
1. 用适当的符号填空
(1) {3, 2, 1} {1, 2, 3} (2) N* Z+
(3) A={x | x是正方形或长方形} B={x | x是矩形}
(4) {0, 1, -1} {x| x =x4}
=
=
=
=
真子集
03
一、引出概念
如果集合A是集合B的子集,并且集合B中至少有一个元素不属于集合A。
则A是B 的真子集。
记作A B (或B A),读作“A 真包含于B”或 “B真包含A”
如: A={1, 2} B={1, 2, 3, 4}
A B A 真包含于B
B A B 真包含A
Venn(维恩)图
注:空集是任何非空集合的真子集。
即,对任何非空集合A, 总有 A
< 小于
> 大于
二、例题讲解
例题1:用适当的符号填空
“ ”,“ ”
(4) {1,3,5} {1, 3, 5, 7} {1, 3, 5, 7, 9}
(5) {1,3,5} {1, 3, 5, 7, 9}
三、课堂练习
1. 解析:
∵ 集合{a,b,c}的所有子集有:
,{a}, {b}, {c}, {a, b}, {a, c}, {b, c},{a, b, c}
∴ 集合{a,b,c}的所有真子集有:
,{a}, {b}, {c}, {a, b}, {a, c}, {b, c}
课堂练
1. 写出集合{a,b,c}的所有子集,指出哪些是它的真子集。
三、课堂练习
课堂练
3.判断下列两个集合之间的关系 ---P9
(1)A={x | x<0}, B={x | x<1}
(2)A={x | x=3k, k∈Z}, B={x | x=6z, z∈N}
(3) A={x∈N+| x是4与10的公倍数}, B={x | x=20m,m∈N+}
三、课堂练习
课堂练
3.判断下列两个集合之间的关系 ---P9
(1)A={x | x<0}, B={x | x<1}
(1) 解析:
A
B
如图:
集合A中的元素都是集合B中的元素,且集合B中至少有一个元素不属于集合A。则A是B的真子集。
A B
三、课堂练习
课堂练
3.判断下列两个集合之间的关系 ---P9
(2)A={x | x=3k, k∈Z}, B={x | x=6z, z∈N}
(2) 解析:
集合A:
∵k∈Z, 令k=...-2,-1,0,1,2,3,4,5,6...
∴x=...-6,-3,0,3,6,9,12,15,18...
∴A={x | x=..-6,-3,0,3,6,9,12,15,18...}
集合B:
∵z∈N,令z=0, 1, 2, 3...
∴x=0, 6, 12, 18...
∴B={x | x=0, 6, 12, 18...}
∴ B是A的真子集。B A,或者A B
三、课堂练习
课堂练
3.判断下列两个集合之间的关系 ---P9
(3) A={x∈N+| x是4与10的公倍数}, B={x | x=20m,m∈N+}
解析:
集合A:
∵ x是4与10的公倍数
∴ x=20, 40,60, 80...
∴ A={x | x=20, 40,60, 80...}
集合B:
∵ m为非0自然数
∴ 令m=1, 2, 3, 4...
∴ B={x | x=20, 40,60, 80...}
∴ A =B
课堂小结
04
课堂小结
集合间的基本关系:子集,相等,真子集
集合与元素的关系:属于“ ∈ ”,不属于“ ”
集合与集合的关系:
子集: “ ” 包含于, “ ” 包含
相等关系: “ = ” 相等
真子集: “ ”真包含于, “ ”真包含
课后作业
05
课后作业
1、判断题
(1)0∈ ( )
(2)0= ( )
(3) {9, 10, 7, 2} ( )
(4){x|x -1=0}与{1}相等 ( )
(5){(0,0)} {(x,y)|x-y=0 ( )
课后作业
2、用适当的符号填空题:
(1) A={x| x+5<10}, B={x| x +1=5}。集合A 集合B
(2)若集合A={x|x -9=0},B={3},C={3,-3}
3 A,B A,C A
3、用Venn图表示下列集合的关系:
A={x|x是正方形},B={x|x是梯形},C={x|x是平行四边形},
D={x|x是矩形},E={x|x是菱形}
课后作业
4、解答题
(1)A={1,2,3},请分别写出集合A所有的子集,真子集。
A的子集个数是多少?非空子集个数是多少?
真子集个数是多少?非空真子集个数是多少?
(2)A={1,2,3,4},请分别写出集合A所有的子集,真子集。
A的子集个数是多少?非空子集个数是多少?
真子集个数是多少?非空真子集个数是多少?
(3)如果A中有a个元素,那么:
A的子集个数是多少?非空子集个数是多少?
真子集个数是多少?非空真子集个数是多少?
课后作业
5、解答题
(1)设m,n∈Z, 若P={1,-m}, W={m, n},P=W。
求m-2n的值
(2)已知集合A={x| -4
低头是题海
抬头是未来
THANKS
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
