数学人教版七年级上册 1.5.2 科学记数法 课件(共19张PPT)
文档属性
| 名称 | 数学人教版七年级上册 1.5.2 科学记数法 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 876.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
1.5.2 科学记数法
第一章 有理数
1.了解科学记数法的意义.
2.会用科学记数法表示较大的数.
光速约三亿米每秒300000000m/s
太阳半径约六十九万六千千米
696000km
新课导入
世界人口约七十亿人7000000000人
谈谈现实生活中遇到的比较大的数有什么呢?
赤道长约4000000 米
地球表面积约510000000平千米
北京故宫占地面积约720000平方米
人体中约有红细胞25000000000000个
思考:这样大的数读、写都不方便,有没有简单的方法表示大数呢?
光速约300000000m/s
太阳半径约696000km
世界人口约7000000000人
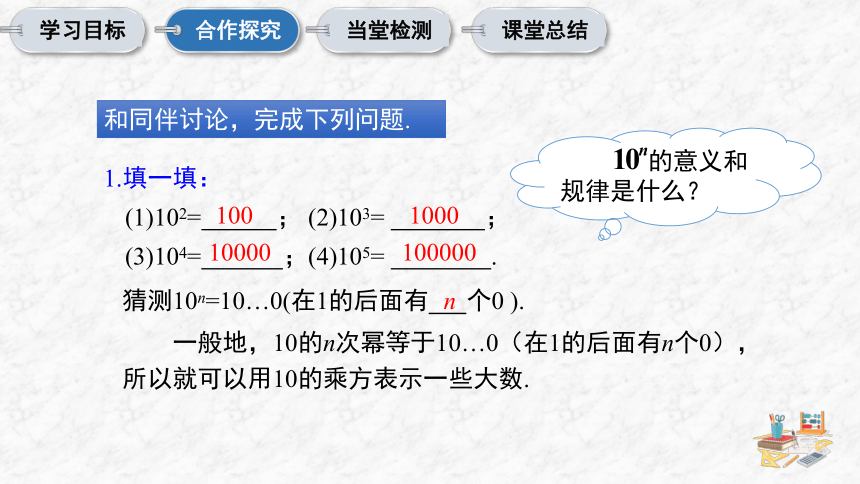
1.填一填:
(1)102= ; (2)103= ;
(3)104= ;(4)105= .
100
1000
10000
100000
猜测10n=10…0(在1的后面有 个0 ).
n
的意义和规律是什么?
一般地,10的n次幂等于10…0(在1的后面有n个0),所以就可以用10的乘方表示一些大数.
和同伴讨论,完成下列问题.
2.通过上面的猜测,你能简单地表示出下面的大数吗?
(1)300000000=3× =3×10( );
(2)696000=696× =6.96×
=6.96×10( );
100000000
8
1000
100000
5
(3) 6100000000=61× =6.1×
=6.1×10( ).
100000000
1000000000
9
3.上面表示的大数有什么特点?它们一般写成什么形式?
这样不仅便于书写简短,同时还便于读数.
像这样,把一个大于10的数表示成 a×10n(其中a大于或等于1且小于10,n为正整数),使用的是科学记数法.
议一议:
怎样用科学记数法表示小于-10的数?
先写出它的相反数,再添加负号就可以了.
例1 下列各数的书写形式是否是科学记数法的形式?如果不是,请说明理由.
(1) 1.5×103; (2) 29×104;
(3) 0.32×103; (4) 2.29×100.
例2 用科学记数法表示下列各数:
1000000, 57000000, -123000000000.
解:
1000000=106,
57000000=5.7×107,
-123000000000=-1.23×1011.
-123000000000=-1.23×1011.
1000000=106,
57000000=5.7×107,
(1)观察上面各式,等号左边整数的位数与等号右边10的指数之间有什么关系?
10的指数比原数的整数位数少1.
(2)如果一个数是6位整数,用科学记数法表示时,1的指数是多少 如果一个数是8位整数呢?
10的指数分别是5、7.
(3)用科学记数法表示一个n位整数时,其中10的指数是 .
n-1
-123000000000=-1.23×1011.
1000000=106,
57000000=5.7×107,
观察上面各式等号两边小数点位置的变化与等号右边10的指数之间有什么关系?
小数点向左移n位,10的指数就是n.
用科学记数法表示下列各数:
试一试:
(4)960万.
(3)23458.2;
(2)-98120000;
(1)3400000;
先确定a的值(1≤ a﹤10),再确定n的值(观察原数整数位数或者小数点移动位数)
思考:一般地,不易读写的大数,可以用科学记数法表示.反过来,已知一个用科学记数法表示的数,你能知道它的原数是多少吗?
归纳:
把用科学记数法表示的数a×10n还原成原数时:
(1) 原数的整数位数等于n+1;
(2) 原数等于把a的小数点向右移动n位所得的数;
小数点向右移动,若位数不够,则用0补上.
将下列用科学记数法表示的数还原成原数.
(4)-4.2×106.
(3)3.6×108;
(2)2.3×107;
(1)1.2×105;
(1)120000;
(2)23000000;
(3)360000000;
(4)-4200000.
练一练
1.用科学记数法表示下列各数.
80000 56000000 7400000
8×104 5.6×107 7.4×106
2.下列用科学记数法表示的数,原来各是什么数?
4×103 8.5×106 7.04×105 3.96×104
4000
8500000
704000
39600
3.太平洋最深处是马里亚纳海沟,它的深度是海平面以下11034米,记为-11034米,用科学记数法表示为( )
A.1.1×104米 B.1.1034×104米
C.-11.034×104米 D.-1.1034×104米
D
4.在以下各数中,最大的数为( )
A.7.2 × 105
B.2.5 × 106
C.9.9 × 105
D.1 × 107
D
5.写出下列用科学记数法表示的数据的原数.
(1)地球绕太阳公转的速度约是1.1×105千米/时;__________
(2)一个正常人一年的心跳次数大约为3.679×107次;__________
(3)世界文化遗产长城总长约6.7×106 m.__________
110000
36790000
670000
6.已知光的传播速度为300000000 m/s,太阳光到达地球的时间大约是500 s,试计算太阳与地球的距离大约是多少千米.(结果用科学记数法表示)
答案:1.5×108km
1.科学记数法:
把一个不易读写的大数表示成a×10n的形式,
这种记数方法叫做科学记数法.
注意:
(1)a只有一位整数数位,即1≤︱a︱< 10;
(2)n的值取决于原数的整数位数,
或原数的小数点向左移动的位数.
2.科学记数法的还原.
1.5.2 科学记数法
第一章 有理数
1.了解科学记数法的意义.
2.会用科学记数法表示较大的数.
光速约三亿米每秒300000000m/s
太阳半径约六十九万六千千米
696000km
新课导入
世界人口约七十亿人7000000000人
谈谈现实生活中遇到的比较大的数有什么呢?
赤道长约4000000 米
地球表面积约510000000平千米
北京故宫占地面积约720000平方米
人体中约有红细胞25000000000000个
思考:这样大的数读、写都不方便,有没有简单的方法表示大数呢?
光速约300000000m/s
太阳半径约696000km
世界人口约7000000000人
1.填一填:
(1)102= ; (2)103= ;
(3)104= ;(4)105= .
100
1000
10000
100000
猜测10n=10…0(在1的后面有 个0 ).
n
的意义和规律是什么?
一般地,10的n次幂等于10…0(在1的后面有n个0),所以就可以用10的乘方表示一些大数.
和同伴讨论,完成下列问题.
2.通过上面的猜测,你能简单地表示出下面的大数吗?
(1)300000000=3× =3×10( );
(2)696000=696× =6.96×
=6.96×10( );
100000000
8
1000
100000
5
(3) 6100000000=61× =6.1×
=6.1×10( ).
100000000
1000000000
9
3.上面表示的大数有什么特点?它们一般写成什么形式?
这样不仅便于书写简短,同时还便于读数.
像这样,把一个大于10的数表示成 a×10n(其中a大于或等于1且小于10,n为正整数),使用的是科学记数法.
议一议:
怎样用科学记数法表示小于-10的数?
先写出它的相反数,再添加负号就可以了.
例1 下列各数的书写形式是否是科学记数法的形式?如果不是,请说明理由.
(1) 1.5×103; (2) 29×104;
(3) 0.32×103; (4) 2.29×100.
例2 用科学记数法表示下列各数:
1000000, 57000000, -123000000000.
解:
1000000=106,
57000000=5.7×107,
-123000000000=-1.23×1011.
-123000000000=-1.23×1011.
1000000=106,
57000000=5.7×107,
(1)观察上面各式,等号左边整数的位数与等号右边10的指数之间有什么关系?
10的指数比原数的整数位数少1.
(2)如果一个数是6位整数,用科学记数法表示时,1的指数是多少 如果一个数是8位整数呢?
10的指数分别是5、7.
(3)用科学记数法表示一个n位整数时,其中10的指数是 .
n-1
-123000000000=-1.23×1011.
1000000=106,
57000000=5.7×107,
观察上面各式等号两边小数点位置的变化与等号右边10的指数之间有什么关系?
小数点向左移n位,10的指数就是n.
用科学记数法表示下列各数:
试一试:
(4)960万.
(3)23458.2;
(2)-98120000;
(1)3400000;
先确定a的值(1≤ a﹤10),再确定n的值(观察原数整数位数或者小数点移动位数)
思考:一般地,不易读写的大数,可以用科学记数法表示.反过来,已知一个用科学记数法表示的数,你能知道它的原数是多少吗?
归纳:
把用科学记数法表示的数a×10n还原成原数时:
(1) 原数的整数位数等于n+1;
(2) 原数等于把a的小数点向右移动n位所得的数;
小数点向右移动,若位数不够,则用0补上.
将下列用科学记数法表示的数还原成原数.
(4)-4.2×106.
(3)3.6×108;
(2)2.3×107;
(1)1.2×105;
(1)120000;
(2)23000000;
(3)360000000;
(4)-4200000.
练一练
1.用科学记数法表示下列各数.
80000 56000000 7400000
8×104 5.6×107 7.4×106
2.下列用科学记数法表示的数,原来各是什么数?
4×103 8.5×106 7.04×105 3.96×104
4000
8500000
704000
39600
3.太平洋最深处是马里亚纳海沟,它的深度是海平面以下11034米,记为-11034米,用科学记数法表示为( )
A.1.1×104米 B.1.1034×104米
C.-11.034×104米 D.-1.1034×104米
D
4.在以下各数中,最大的数为( )
A.7.2 × 105
B.2.5 × 106
C.9.9 × 105
D.1 × 107
D
5.写出下列用科学记数法表示的数据的原数.
(1)地球绕太阳公转的速度约是1.1×105千米/时;__________
(2)一个正常人一年的心跳次数大约为3.679×107次;__________
(3)世界文化遗产长城总长约6.7×106 m.__________
110000
36790000
670000
6.已知光的传播速度为300000000 m/s,太阳光到达地球的时间大约是500 s,试计算太阳与地球的距离大约是多少千米.(结果用科学记数法表示)
答案:1.5×108km
1.科学记数法:
把一个不易读写的大数表示成a×10n的形式,
这种记数方法叫做科学记数法.
注意:
(1)a只有一位整数数位,即1≤︱a︱< 10;
(2)n的值取决于原数的整数位数,
或原数的小数点向左移动的位数.
2.科学记数法的还原.
