人教版(2019)必修第二册 5.2.1 运动的合成与分解 课件(共20张PPT)
文档属性
| 名称 | 人教版(2019)必修第二册 5.2.1 运动的合成与分解 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-28 17:16:25 | ||
图片预览







文档简介
(共20张PPT)
1.曲线运动是轨迹为 的运动.
2.曲线运动的速度方向是 的,但速度的大小可以改变也可以不改变。
3.质点在某一点(或某一时刻)的速度方向是在曲线上这一点的 上
4.曲线运动一定是 运动,一定有_______。
5.物体做曲线运动的条件: 运动物体所受合外力的方向跟它的速度方向 __________ 上 。
变速
曲线
时刻改变
切线方向
不在同一直线
加速度
6.曲线运动的轨迹向______方向弯曲。
合力
复习回顾
5.1 运动的合成与分解A
A'
人在游泳池中始终保持头朝正前方游向对岸A',他能到达吗A'?
A'
若人在河中始终保持头朝正前方游向对岸A',他能到达吗A'?
0
x
y
θ
θ
Vx
Vy
V
P
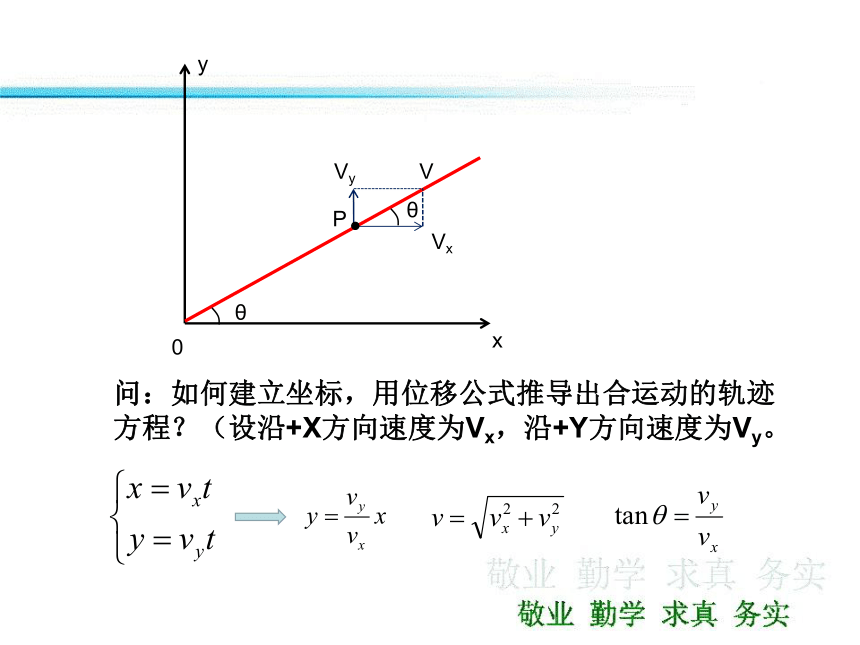
问:如何建立坐标,用位移公式推导出合运动的轨迹方程?(设沿+X方向速度为Vx,沿+Y方向速度为Vy。
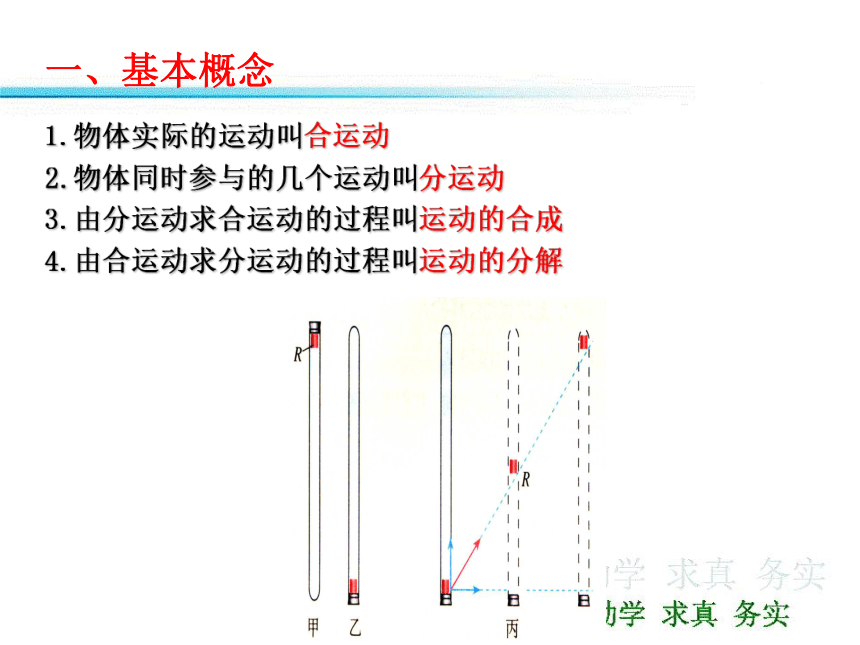
1.物体实际的运动叫合运动
2.物体同时参与的几个运动叫分运动
3.由分运动求合运动的过程叫运动的合成
4.由合运动求分运动的过程叫运动的分解
一、基本概念
请画出蜡块的运动轨迹。
典型问题:小船过河
例1:一艘小船在宽为 d 的河中横渡到对岸,已知水流速度是V水,小船在静水中的速度是V船,(V水(1)船头垂直河岸,小船渡河需要多少时间?到达对岸的位置在哪里?
分析1:船头垂直河岸
d
最短时间
例1:一艘小船在宽为 d 的河中横渡到对岸,已知水流速度是V水,小船在静水中的速度是V船,(V水<V船),求:
(2)欲使船到达正对岸,船应该怎样渡河,需要多少时间?
分析2:到达正对岸
θ
d
设船头指向与上游河岸成θ:
结论:当合速度V垂直河岸时,到达正对岸。
最短距离
拓展:
1.在船头始终垂直对岸的情况下,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
2.为了垂直到达河对岸,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
3.如果小船船头垂直河岸,以初速度为零,匀加速始向对岸,请画出大致的运动轨迹?
答案:变长
答案:不变
答案:抛物线
运动的合成与分解是指位移、速度、加速度的合成与分解。
二、运算法则:
(1)两个分运动在同一直线上时,同向相加,反向相减。
(2)不在同一直线上,按照平行四边形定则合成或分解。
同时性
独立性
等效性
同体性
合运动所需时间和对应的每个分运动所需时间相等
一个物体可以同时参与几个不同的分运动,各个分运动独立进行,互不影响
合运动与分运动在效果上是等效替代的关系
合运动与分运动必须对同一物体
三、合运动与分运动的关系
例2:一艘小船在宽为 d 的河中横渡到对岸,已知水流速度是V水,小船在静水中的速度是V船,(V水>V船),求:
(2)欲使小船过河距离最短,船应该怎样渡河?
θ
θ
结论:当v船< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
1.曲线运动是轨迹为 的运动.
2.曲线运动的速度方向是 的,但速度的大小可以改变也可以不改变。
3.质点在某一点(或某一时刻)的速度方向是在曲线上这一点的 上
4.曲线运动一定是 运动,一定有_______。
5.物体做曲线运动的条件: 运动物体所受合外力的方向跟它的速度方向 __________ 上 。
变速
曲线
时刻改变
切线方向
不在同一直线
加速度
6.曲线运动的轨迹向______方向弯曲。
合力
复习回顾
5.1 运动的合成与分解A
A'
人在游泳池中始终保持头朝正前方游向对岸A',他能到达吗A'?
A'
若人在河中始终保持头朝正前方游向对岸A',他能到达吗A'?
0
x
y
θ
θ
Vx
Vy
V
P
问:如何建立坐标,用位移公式推导出合运动的轨迹方程?(设沿+X方向速度为Vx,沿+Y方向速度为Vy。
1.物体实际的运动叫合运动
2.物体同时参与的几个运动叫分运动
3.由分运动求合运动的过程叫运动的合成
4.由合运动求分运动的过程叫运动的分解
一、基本概念
请画出蜡块的运动轨迹。
典型问题:小船过河
例1:一艘小船在宽为 d 的河中横渡到对岸,已知水流速度是V水,小船在静水中的速度是V船,(V水
分析1:船头垂直河岸
d
最短时间
例1:一艘小船在宽为 d 的河中横渡到对岸,已知水流速度是V水,小船在静水中的速度是V船,(V水<V船),求:
(2)欲使船到达正对岸,船应该怎样渡河,需要多少时间?
分析2:到达正对岸
θ
d
设船头指向与上游河岸成θ:
结论:当合速度V垂直河岸时,到达正对岸。
最短距离
拓展:
1.在船头始终垂直对岸的情况下,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
2.为了垂直到达河对岸,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
3.如果小船船头垂直河岸,以初速度为零,匀加速始向对岸,请画出大致的运动轨迹?
答案:变长
答案:不变
答案:抛物线
运动的合成与分解是指位移、速度、加速度的合成与分解。
二、运算法则:
(1)两个分运动在同一直线上时,同向相加,反向相减。
(2)不在同一直线上,按照平行四边形定则合成或分解。
同时性
独立性
等效性
同体性
合运动所需时间和对应的每个分运动所需时间相等
一个物体可以同时参与几个不同的分运动,各个分运动独立进行,互不影响
合运动与分运动在效果上是等效替代的关系
合运动与分运动必须对同一物体
三、合运动与分运动的关系
例2:一艘小船在宽为 d 的河中横渡到对岸,已知水流速度是V水,小船在静水中的速度是V船,(V水>V船),求:
(2)欲使小船过河距离最短,船应该怎样渡河?
θ
θ
结论:当v船< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
