1.2.2数轴 课件(共14张PPT)数学人教版 七年级上册
文档属性
| 名称 | 1.2.2数轴 课件(共14张PPT)数学人教版 七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
人教版 七年级上册
第一章 有理数
1.2.1 数轴
复习提问 :
1 、什么叫做有理数?
整数 与 分数 统称为 有理数
2 、有理数根据 符号 可以分成哪三类?
正有理数、负有理数、0。
3、请问温度计显示 零上 20 ℃ 、 零下 5 摄氏度 时,你如何用有理数来表示?
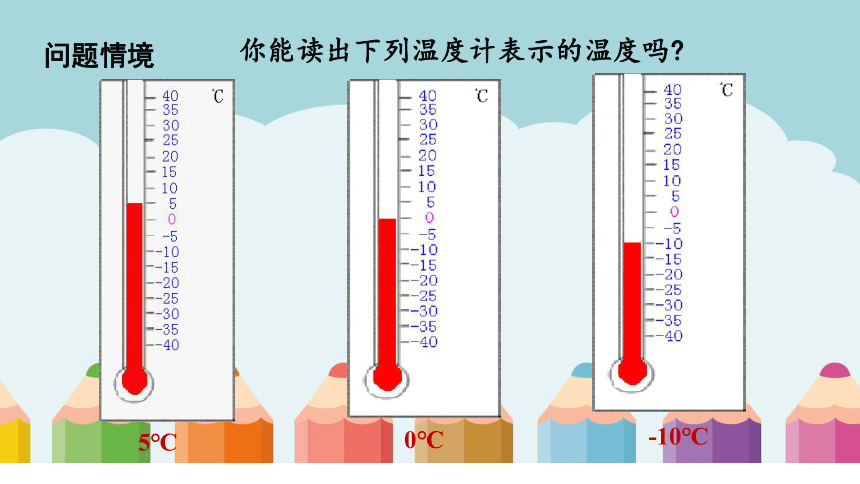
问题情境
你能读出下列温度计表示的温度吗
5℃
0℃
-10℃
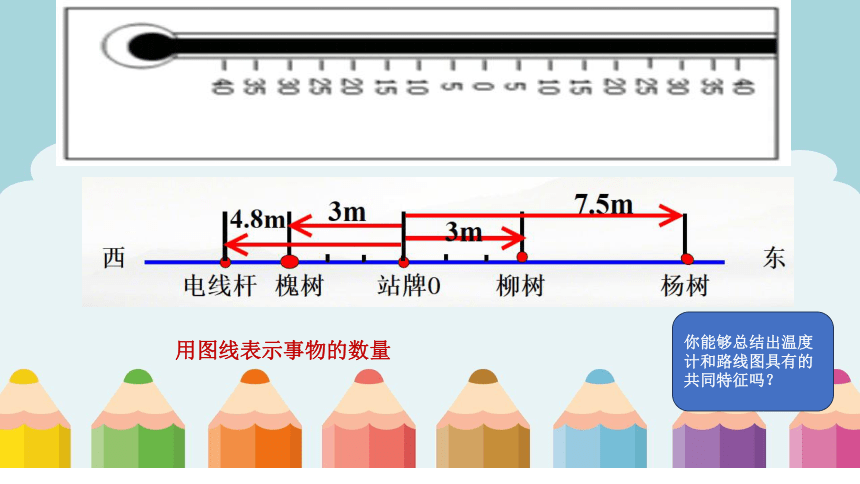
问题:在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站牌西3m和4.8m处分别有一颗槐树和一根电线杆,试画图表示这一情景。
你能够总结出温度计和路线图具有的共同特征吗?
用图线表示事物的数量
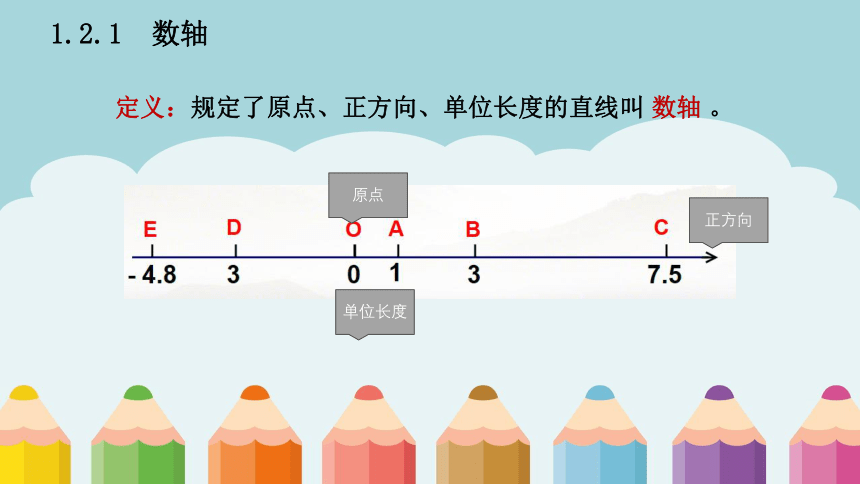
数轴
(1)图中的 0 点,相当于0 0 C或出发点的点,叫做 原点 ;
(2)规定了 正方向 。
图中从原点向右为正方向,向左为负方向。
(3)选取了适当长度作为 单位长度 , 相当于温度计的1 ℃ 占1小格的长度。
1.2.1 数轴
定义:规定了原点、正方向、单位长度的直线叫 数轴 。
正方向
单位长度
原点
1.2.1 数轴
数轴的画法:
一般地,表示正数的点在原点的____边,
表示负数的点在原点的____边,
数轴上点所表示的数从左往右逐渐____
1.2.1 数轴
例 1 、判断下列各图,哪个是数轴,哪个不是数轴。
1.2.1 数轴(用数轴上的点表示数)
例 2 、在数轴上画出表示下列各数的点:
数 数轴上的点
1.2.1 数轴(用数表示数轴上的点)
例 3 、写出下面数轴上的 A 、 B 、 C 、 D 、 E 、 F 各点表示的数。
数轴上的点 数
体现了 数形结合 的思想
练习1 . 在数轴上有三个点 A , B , C ,如图所示:
(1)点C距离原点有______个单位长度;
(2)不小于点A表示的数的负整数是___________;
(3)将点B向右移1个单位长度,此时该点表示的数是___;再向左移5个单位长度,此时该点表示的数是_____.这两点间距离是_____个单位长度
练习2、在数轴上,到原点的距离等于 4 个单位长度的点所表示的数是( )。
A 、 +4 , B 、 -4 ,
C 、 +2 或 -2 D 、 +4 或 -4
课堂小结:
数轴是什么?
数轴“三要素”各指什么?
怎样画数轴?描点时哪些数容易描错?
人教版 七年级上册
第一章 有理数
1.2.1 数轴
复习提问 :
1 、什么叫做有理数?
整数 与 分数 统称为 有理数
2 、有理数根据 符号 可以分成哪三类?
正有理数、负有理数、0。
3、请问温度计显示 零上 20 ℃ 、 零下 5 摄氏度 时,你如何用有理数来表示?
问题情境
你能读出下列温度计表示的温度吗
5℃
0℃
-10℃
问题:在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站牌西3m和4.8m处分别有一颗槐树和一根电线杆,试画图表示这一情景。
你能够总结出温度计和路线图具有的共同特征吗?
用图线表示事物的数量
数轴
(1)图中的 0 点,相当于0 0 C或出发点的点,叫做 原点 ;
(2)规定了 正方向 。
图中从原点向右为正方向,向左为负方向。
(3)选取了适当长度作为 单位长度 , 相当于温度计的1 ℃ 占1小格的长度。
1.2.1 数轴
定义:规定了原点、正方向、单位长度的直线叫 数轴 。
正方向
单位长度
原点
1.2.1 数轴
数轴的画法:
一般地,表示正数的点在原点的____边,
表示负数的点在原点的____边,
数轴上点所表示的数从左往右逐渐____
1.2.1 数轴
例 1 、判断下列各图,哪个是数轴,哪个不是数轴。
1.2.1 数轴(用数轴上的点表示数)
例 2 、在数轴上画出表示下列各数的点:
数 数轴上的点
1.2.1 数轴(用数表示数轴上的点)
例 3 、写出下面数轴上的 A 、 B 、 C 、 D 、 E 、 F 各点表示的数。
数轴上的点 数
体现了 数形结合 的思想
练习1 . 在数轴上有三个点 A , B , C ,如图所示:
(1)点C距离原点有______个单位长度;
(2)不小于点A表示的数的负整数是___________;
(3)将点B向右移1个单位长度,此时该点表示的数是___;再向左移5个单位长度,此时该点表示的数是_____.这两点间距离是_____个单位长度
练习2、在数轴上,到原点的距离等于 4 个单位长度的点所表示的数是( )。
A 、 +4 , B 、 -4 ,
C 、 +2 或 -2 D 、 +4 或 -4
课堂小结:
数轴是什么?
数轴“三要素”各指什么?
怎样画数轴?描点时哪些数容易描错?
