24.3.2.1相似三角形的识别1(广东省佛山市顺德区)
文档属性
| 名称 | 24.3.2.1相似三角形的识别1(广东省佛山市顺德区) |

|
|
| 格式 | rar | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-01 00:00:00 | ||
图片预览



文档简介
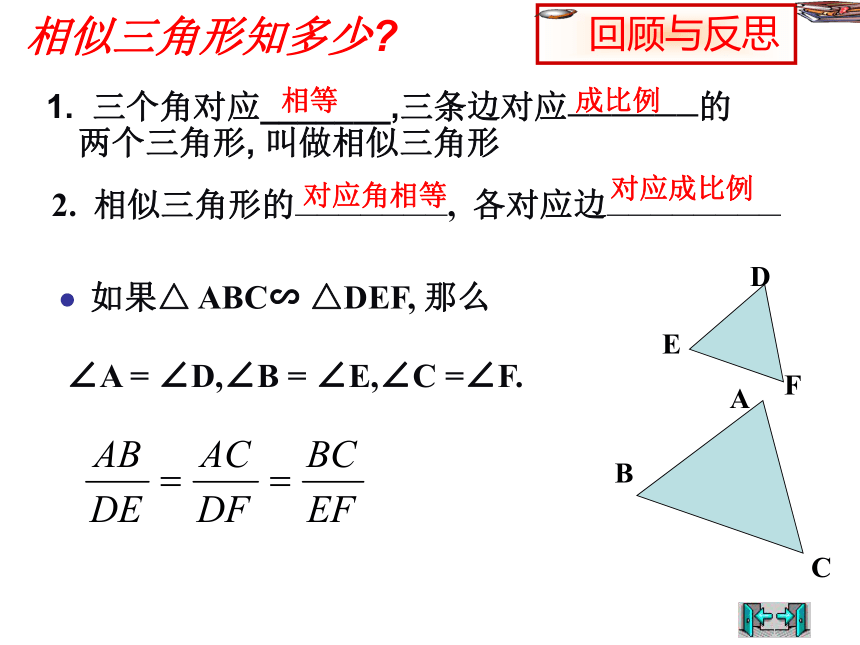
课件20张PPT。 相似三角形的识别(1)相似三角形知多少?1. 三个角对应_______,三条边对应——————的两个三角形, 叫做相似三角形 相等成比例对应角相等对应成比例 如果△ ABC∽ △DEF, 那么2. 相似三角形的———————, 各对应边————————∠A = ∠D,∠B = ∠E,∠C =∠F.ABCDEF1. △ ABC与△ DEF相似,且相似比是则△ DEF 与△ ABC与的相似比是( )2、如何识别两个多边形相似呢?
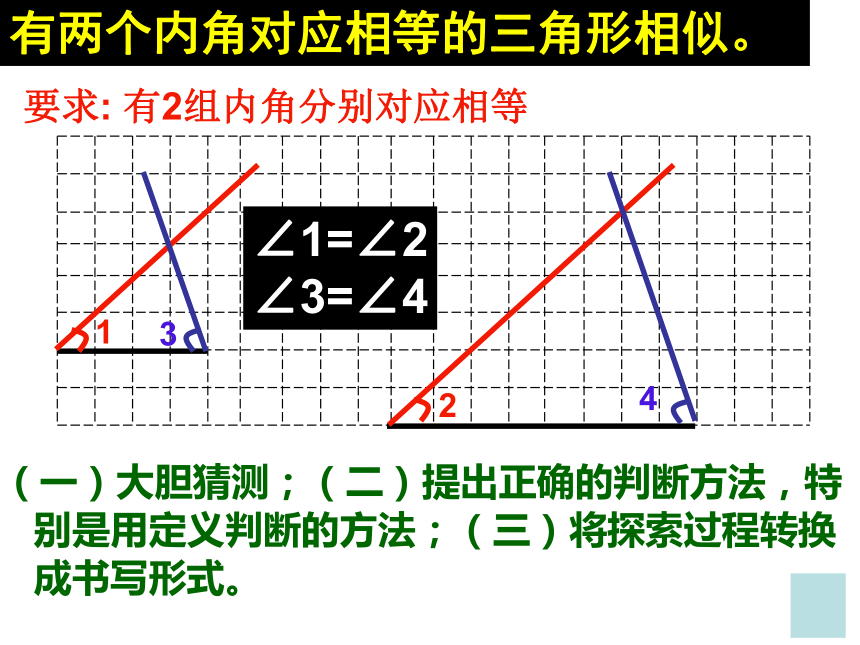
两个多边形对应角相等,对应边成比例3、如何识别两个三角形相似呢?有两个内角对应相等的三角形相似。1243∠1=∠2
∠3=∠4要求: 有2组内角分别对应相等(一)大胆猜测;(二)提出正确的判断方法,特别是用定义判断的方法;(三)将探索过程转换成书写形式。得出结论:
有两个角对应相等的两个三角形的对应角相等,对应边成比例。
即:有两角对应相等的两个三角形相似。
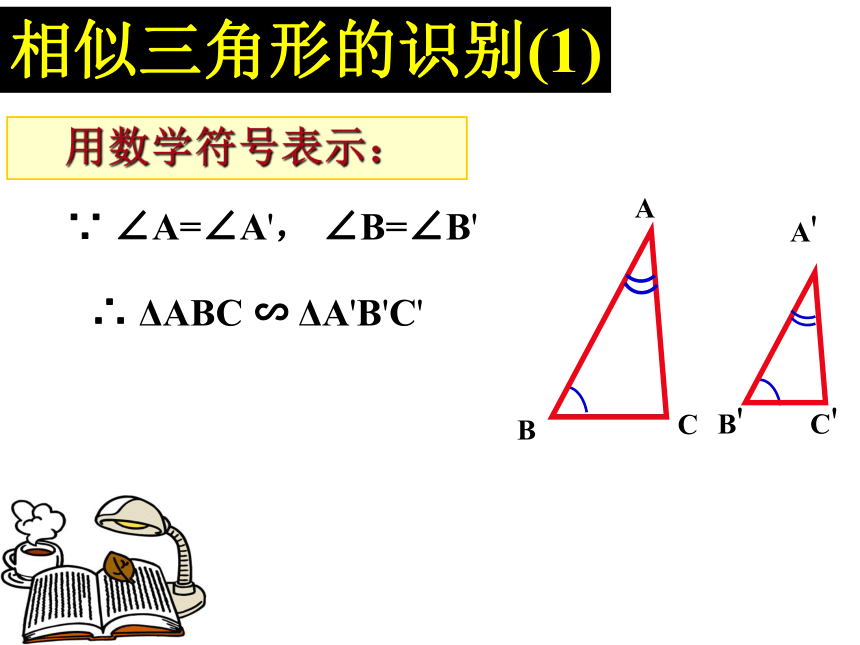
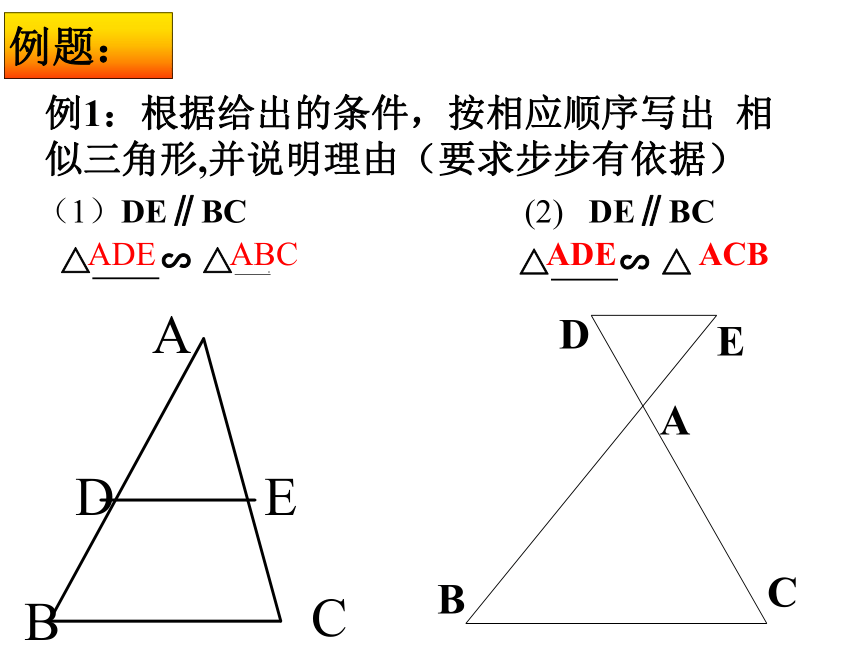
CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别(1)例1:根据给出的条件,按相应顺序写出 相似三角形,并说明理由(要求步步有依据)AEDCB(2) DE∥BC
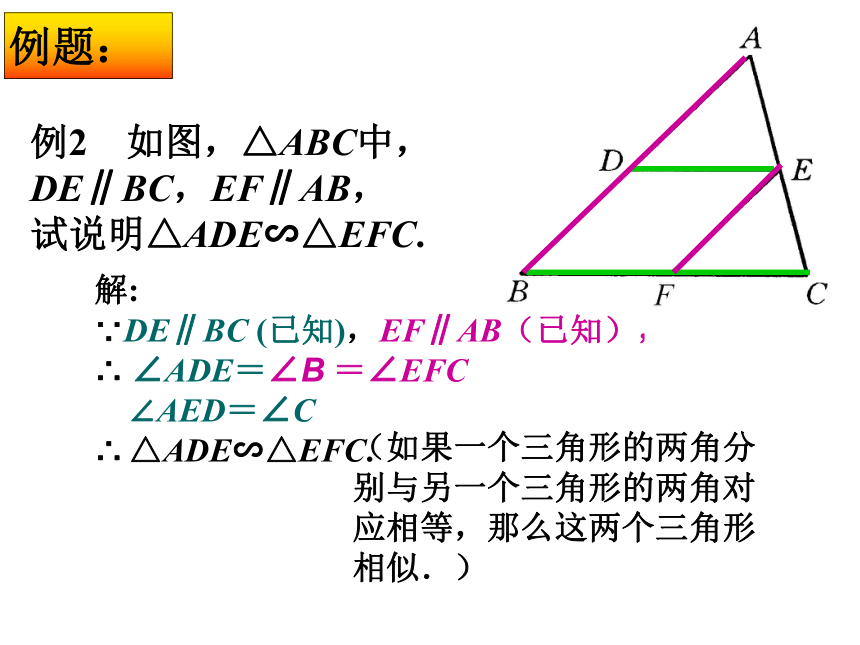
△ ∽ △ △ ∽ △ . (1)DE∥BC ADE ABCADE ACB例2 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解:
∵DE∥BC (已知),EF∥AB(已知),
∴ ∠ADE=∠B =∠EFC
∠AED=∠C
∴ △ADE∽△EFC.
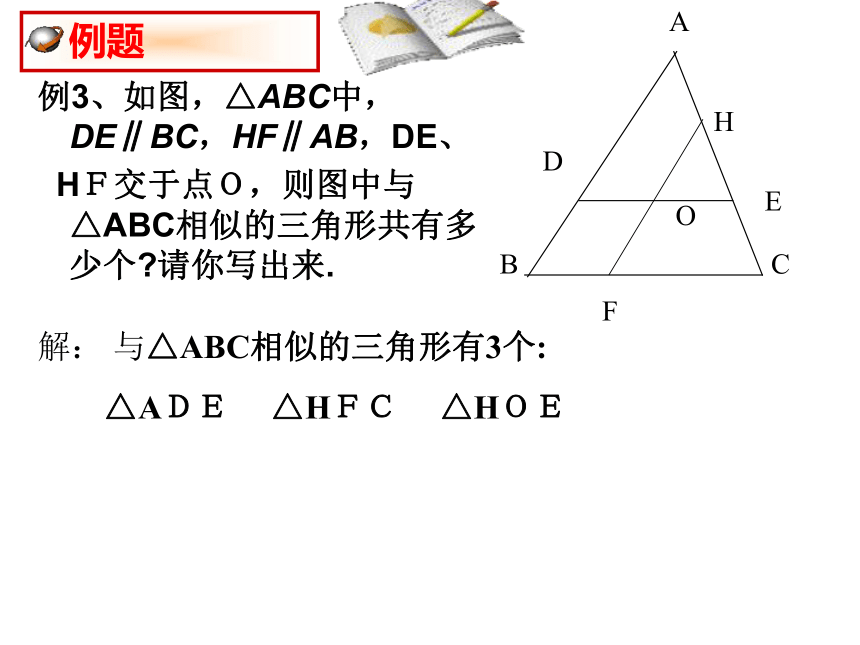
(如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.) 例3、如图,△ABC中,DE∥BC,HF∥AB,DE、
HF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个:
△ADE △HFC △HOE 例4、 如图,△ABC中,点D是AB上一点.(1)若∠1=∠B,写出图中的相似三角形.解:图中的相似三角形有:⊿ABC与⊿ACD其理由:∵∠A=∠A,∠B=∠1
∴△ABC~△ACD 例4、 如图,△ABC中,点D是AB上一点.如图,若有∠1= ∠B= ∠2,写出图中的相似三角形.解:图中的相似三角形有:
⊿ABC∽⊿ACD∽⊿ADE如图,若有∠C= ∠2,写出图中的相似三角形.解:图中的相似三角形有:⊿ABC∽⊿AED变式1 如图,△ABC中,点D是AB上一点,且∠1=∠B。 3) 若:AD=16, DB=9. 求AC的长.2) 说明 : AC2=AD·AB
1) 说明: ∴△ABC~△ACD解: ∵∠A=∠A,∠B=∠1
∴△ABC~△ACD解: 由1)知: △ABC~△ACD
∴ AB:AC=AC:AD.则 AC2=AD·AB解: 由2)知:AC2=AD·AB=16(16+9)=16×25
所以 AC=20.变式2: 如图,△ABC中,点D是AB上一点,且∠ACB=900,CD⊥AB.
试说明:⊿ABC∽⊿ACD∽⊿BCD
12结论: 直角三角形斜边上的高分成的两个直角三角形与原三角形相似你得什么结论?(1)ΔABC和ΔDEF中,
∠A=400,∠B=800,
∠E=800, ∠F=600。
ΔABC与ΔDEF 。 练习1(2) D为ΔABC边AB上的一点,
且∠ACD=∠B ,
则ΔABC与ΔACD ________.
相似相似(填: “相似”或“不相似”, 并说明理由)。 3.如图(1),AE与BD相交于点C,要△ABC∽△DEC,需要条件 ;
4.已知,如图(2)要△ABC∽△ACD,
需要条件 ;
5.已知,如图(3)要使△ABE∽△ACD,
需要条件 ;
))2、判断题:
1.所有的等腰三角形都相似。( )
2.所有的等腰直角三角形都相似。( )
3.所有的等边三角形都相似。( )
4.所有的直角三角形都相似。( )
5.有一个角是100°的两个等腰三角形相似。( )
6.有一个角是70°的两个等腰三角形相似。( )
在△ABC中,DE//BC,M是BC的中点,AM交
DE于N,试说明DN=ENADEBCNM
两个多边形对应角相等,对应边成比例3、如何识别两个三角形相似呢?有两个内角对应相等的三角形相似。1243∠1=∠2
∠3=∠4要求: 有2组内角分别对应相等(一)大胆猜测;(二)提出正确的判断方法,特别是用定义判断的方法;(三)将探索过程转换成书写形式。得出结论:
有两个角对应相等的两个三角形的对应角相等,对应边成比例。
即:有两角对应相等的两个三角形相似。
CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别(1)例1:根据给出的条件,按相应顺序写出 相似三角形,并说明理由(要求步步有依据)AEDCB(2) DE∥BC
△ ∽ △ △ ∽ △ . (1)DE∥BC ADE ABCADE ACB例2 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解:
∵DE∥BC (已知),EF∥AB(已知),
∴ ∠ADE=∠B =∠EFC
∠AED=∠C
∴ △ADE∽△EFC.
(如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.) 例3、如图,△ABC中,DE∥BC,HF∥AB,DE、
HF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个:
△ADE △HFC △HOE 例4、 如图,△ABC中,点D是AB上一点.(1)若∠1=∠B,写出图中的相似三角形.解:图中的相似三角形有:⊿ABC与⊿ACD其理由:∵∠A=∠A,∠B=∠1
∴△ABC~△ACD 例4、 如图,△ABC中,点D是AB上一点.如图,若有∠1= ∠B= ∠2,写出图中的相似三角形.解:图中的相似三角形有:
⊿ABC∽⊿ACD∽⊿ADE如图,若有∠C= ∠2,写出图中的相似三角形.解:图中的相似三角形有:⊿ABC∽⊿AED变式1 如图,△ABC中,点D是AB上一点,且∠1=∠B。 3) 若:AD=16, DB=9. 求AC的长.2) 说明 : AC2=AD·AB
1) 说明: ∴△ABC~△ACD解: ∵∠A=∠A,∠B=∠1
∴△ABC~△ACD解: 由1)知: △ABC~△ACD
∴ AB:AC=AC:AD.则 AC2=AD·AB解: 由2)知:AC2=AD·AB=16(16+9)=16×25
所以 AC=20.变式2: 如图,△ABC中,点D是AB上一点,且∠ACB=900,CD⊥AB.
试说明:⊿ABC∽⊿ACD∽⊿BCD
12结论: 直角三角形斜边上的高分成的两个直角三角形与原三角形相似你得什么结论?(1)ΔABC和ΔDEF中,
∠A=400,∠B=800,
∠E=800, ∠F=600。
ΔABC与ΔDEF 。 练习1(2) D为ΔABC边AB上的一点,
且∠ACD=∠B ,
则ΔABC与ΔACD ________.
相似相似(填: “相似”或“不相似”, 并说明理由)。 3.如图(1),AE与BD相交于点C,要△ABC∽△DEC,需要条件 ;
4.已知,如图(2)要△ABC∽△ACD,
需要条件 ;
5.已知,如图(3)要使△ABE∽△ACD,
需要条件 ;
))2、判断题:
1.所有的等腰三角形都相似。( )
2.所有的等腰直角三角形都相似。( )
3.所有的等边三角形都相似。( )
4.所有的直角三角形都相似。( )
5.有一个角是100°的两个等腰三角形相似。( )
6.有一个角是70°的两个等腰三角形相似。( )
在△ABC中,DE//BC,M是BC的中点,AM交
DE于N,试说明DN=ENADEBCNM
