人教版(2019)必修第二册 8.4 机械能守恒定律 课件(共20张PPT)
文档属性
| 名称 | 人教版(2019)必修第二册 8.4 机械能守恒定律 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-28 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第四节 机械能守恒定律
--动能定理的特例
规律推导:以单摆为模型,用动能定理进行推导
*
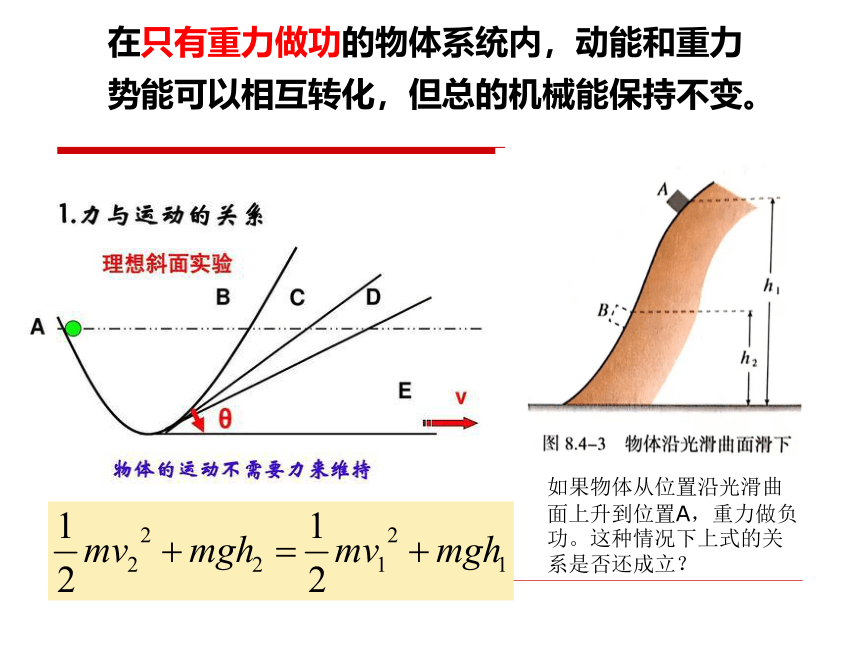
在只有重力做功的物体系统内,动能和重力势能可以相互转化,但总的机械能保持不变。?
如果物体从位置沿光滑曲面上升到位置A,重力做负功。这种情况下上式的关系是否还成立?
分析弹簧小球水平振动
1、小球完成一个全振动可分为几个过程?
2、每个过程中能量是怎样变化的?
在系统内只有弹簧的弹力做功的物体系统内,物体的动能和弹性势能可以相互转化,但机械能的总量也保持不变。
1.定义:物体的动能和势能之和称为物体的机械能。
机械能包括动能、重力势能、弹性势能。
2.表达式:E=EK+EP
3.机械能是标量,具有相对性:
先选取参考平面和参考系(一般选地面)才能确定机械能。
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变,这个结论叫做机械能守恒定律。?
总结归纳:
(一).机械能守恒定律的表达形式
(1)系统在初状态的总机械能等于末状态的总机械能
用⑴时,需要规定重力势能的参考平面。
(2)物体(或系统)增加的动能等于物 体(或系统)减少的势能,反之亦然。
ΔEK = -ΔEP
用⑵时则不必规定重力势能的参考平面,因为重力势能的改变量与参考平面的选取没有关系。
(二)、机械能守恒的条件的理解
条件:只有重力(或弹力)做功
只有重力和弹力做功可作如下三层理解:
(1)只受重力作用
在不考虑空气阻力的情况下的各种抛体运动——自由落体、竖直上抛、平抛、斜抛等等。
(2)受其他力,但其他力不做功,只有重力或弹力做功
①物体沿光滑的曲面下滑,受重力、曲面的支持力的作用,但曲面的支持力不做功。
②在光滑水平面上的小球碰到弹簧,把弹簧压缩后又被弹簧弹回来。
例1.下列运动物体,机械能守恒的有( )
A.物体沿斜面匀速下滑
B.物体沿竖直平面内的圆形轨道做匀速圆周运动
C.跳伞运动员在空中匀速下落
D.沿光滑曲面自由下滑的木块
E.在拉力作用下,物体沿斜面匀速上滑的过程
D
例2.如下图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,下列关于能量的叙述中正确的是(不计阻力) ( )
(A)重力势能和动能之和总保持不变
(B)重力势能和弹性势能之和总保持不变
(C)动能和弹性势能之和总保持不变
(D)重力势能、弹性势能和动能
之和总保持不变
D
例3:如图所示,把一个小球用细线悬挂起来,就成为一个摆,摆长为L,最大偏角为θ。如果阻力可以忽略
(1)小球运动到最低位置时的速度是多大
(2)在最低点,细线的拉力为多大
利用机械能守恒定律的解题步骤:
①选取研究对象和研究过程。
②根据研究对象所经历的物理过程,进行受力,做功分析,判断机械能是否守恒。
③选取合适的参考平面,确定研究对象在过程的初、末态时的机械能。
④根据机械能守恒定律列方程,进行求解。
例4:如图所示,轻质细杆的两端分别固定质量均为m的两个小球A和B,细杆可绕O轴在竖直平面内无摩擦地自由转动,BO=2AO=2L,将细杆从水平静止状态自由释放,求细杆转到竖直位置时,两球的速度大小。
例5:一根质量不计的细杆长为2 L,一端固定在光滑的水平转轴O上。在杆的另一端和杆的中点各固定一个质量为m的小球,然后使杆从水平位置由静止开始,在竖直平面内自由下摆,如图所示。试求:(1)杆从水平位置向下摆至竖直位置时,两球的速度大小;(2)杆从水平位置向下摆至竖直位置的过程中,杆对球B所做的功;(3)杆从水平位置向下摆至竖直位置时,OA与OB两杆的张力之比。
例5:如图所示,质量分别为2m和3m的两个小球固定在一根直角尺的两端A、 B,直角尺的顶点O处有光滑的固定转动轴。AO、BO的长分别为2L和L。开始时直角尺的AO部分处于水平位置而B在O的正下方。让该系统由静止开始自由转动,求:
(1)当A到达最低点时,A小球的速度大小vA;
(2)B球能上升的最大高度h;
(3)开始转动后B球可能达到的最大速度vm。
练:把质量为0.5kg的石块从10m高处以 角斜向上方抛出(如图),初速度是 .
不计空气阻力. (1)石块落地时的速度是多大?请用机械能守恒定律和动能定理分别讨论. (2)石块落地时速度的大小与下列哪些量有关,与哪些量无关?说明理由. A.石块的质量.
B.石块初速度的大小. C.石块初速度的仰角.
D.石块抛出时的高度.
15m/s
A、C
练:如图所示,用长为L的轻绳,一端拴一个质量为m的小球,一端固定在O点,小球从最低点开始运动,若小球刚好能通过最高点,在竖直平面内做圆周运动,求:
(1)小球通过最高点的向心力;
(2)小球通过最高点的速度;
(3)小球通过最低点的速度。
(4)小球通过最低点时受到绳子的拉力。
1、机械能守恒定律
2、机械能守恒定律表达式
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变,这个结论叫做机械能守恒定律。?
ΔEK = -ΔEP
小 结
练:神舟号载人飞船在发射至返回的过程中,以下哪些阶段返回舱的机械能守恒
A. 飞船升空的阶段 B. 飞船在椭圆轨道上绕地球运行的阶段 C. 返回舱在大气层外向着地球做无动力飞行阶段 D. 降落伞张开后,返回舱下降的阶段
B、C
第四节 机械能守恒定律
--动能定理的特例
规律推导:以单摆为模型,用动能定理进行推导
*
在只有重力做功的物体系统内,动能和重力势能可以相互转化,但总的机械能保持不变。?
如果物体从位置沿光滑曲面上升到位置A,重力做负功。这种情况下上式的关系是否还成立?
分析弹簧小球水平振动
1、小球完成一个全振动可分为几个过程?
2、每个过程中能量是怎样变化的?
在系统内只有弹簧的弹力做功的物体系统内,物体的动能和弹性势能可以相互转化,但机械能的总量也保持不变。
1.定义:物体的动能和势能之和称为物体的机械能。
机械能包括动能、重力势能、弹性势能。
2.表达式:E=EK+EP
3.机械能是标量,具有相对性:
先选取参考平面和参考系(一般选地面)才能确定机械能。
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变,这个结论叫做机械能守恒定律。?
总结归纳:
(一).机械能守恒定律的表达形式
(1)系统在初状态的总机械能等于末状态的总机械能
用⑴时,需要规定重力势能的参考平面。
(2)物体(或系统)增加的动能等于物 体(或系统)减少的势能,反之亦然。
ΔEK = -ΔEP
用⑵时则不必规定重力势能的参考平面,因为重力势能的改变量与参考平面的选取没有关系。
(二)、机械能守恒的条件的理解
条件:只有重力(或弹力)做功
只有重力和弹力做功可作如下三层理解:
(1)只受重力作用
在不考虑空气阻力的情况下的各种抛体运动——自由落体、竖直上抛、平抛、斜抛等等。
(2)受其他力,但其他力不做功,只有重力或弹力做功
①物体沿光滑的曲面下滑,受重力、曲面的支持力的作用,但曲面的支持力不做功。
②在光滑水平面上的小球碰到弹簧,把弹簧压缩后又被弹簧弹回来。
例1.下列运动物体,机械能守恒的有( )
A.物体沿斜面匀速下滑
B.物体沿竖直平面内的圆形轨道做匀速圆周运动
C.跳伞运动员在空中匀速下落
D.沿光滑曲面自由下滑的木块
E.在拉力作用下,物体沿斜面匀速上滑的过程
D
例2.如下图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,下列关于能量的叙述中正确的是(不计阻力) ( )
(A)重力势能和动能之和总保持不变
(B)重力势能和弹性势能之和总保持不变
(C)动能和弹性势能之和总保持不变
(D)重力势能、弹性势能和动能
之和总保持不变
D
例3:如图所示,把一个小球用细线悬挂起来,就成为一个摆,摆长为L,最大偏角为θ。如果阻力可以忽略
(1)小球运动到最低位置时的速度是多大
(2)在最低点,细线的拉力为多大
利用机械能守恒定律的解题步骤:
①选取研究对象和研究过程。
②根据研究对象所经历的物理过程,进行受力,做功分析,判断机械能是否守恒。
③选取合适的参考平面,确定研究对象在过程的初、末态时的机械能。
④根据机械能守恒定律列方程,进行求解。
例4:如图所示,轻质细杆的两端分别固定质量均为m的两个小球A和B,细杆可绕O轴在竖直平面内无摩擦地自由转动,BO=2AO=2L,将细杆从水平静止状态自由释放,求细杆转到竖直位置时,两球的速度大小。
例5:一根质量不计的细杆长为2 L,一端固定在光滑的水平转轴O上。在杆的另一端和杆的中点各固定一个质量为m的小球,然后使杆从水平位置由静止开始,在竖直平面内自由下摆,如图所示。试求:(1)杆从水平位置向下摆至竖直位置时,两球的速度大小;(2)杆从水平位置向下摆至竖直位置的过程中,杆对球B所做的功;(3)杆从水平位置向下摆至竖直位置时,OA与OB两杆的张力之比。
例5:如图所示,质量分别为2m和3m的两个小球固定在一根直角尺的两端A、 B,直角尺的顶点O处有光滑的固定转动轴。AO、BO的长分别为2L和L。开始时直角尺的AO部分处于水平位置而B在O的正下方。让该系统由静止开始自由转动,求:
(1)当A到达最低点时,A小球的速度大小vA;
(2)B球能上升的最大高度h;
(3)开始转动后B球可能达到的最大速度vm。
练:把质量为0.5kg的石块从10m高处以 角斜向上方抛出(如图),初速度是 .
不计空气阻力. (1)石块落地时的速度是多大?请用机械能守恒定律和动能定理分别讨论. (2)石块落地时速度的大小与下列哪些量有关,与哪些量无关?说明理由. A.石块的质量.
B.石块初速度的大小. C.石块初速度的仰角.
D.石块抛出时的高度.
15m/s
A、C
练:如图所示,用长为L的轻绳,一端拴一个质量为m的小球,一端固定在O点,小球从最低点开始运动,若小球刚好能通过最高点,在竖直平面内做圆周运动,求:
(1)小球通过最高点的向心力;
(2)小球通过最高点的速度;
(3)小球通过最低点的速度。
(4)小球通过最低点时受到绳子的拉力。
1、机械能守恒定律
2、机械能守恒定律表达式
在只有重力或弹力做功的物体系统内,动能和势能可以相互转化,而总的机械能保持不变,这个结论叫做机械能守恒定律。?
ΔEK = -ΔEP
小 结
练:神舟号载人飞船在发射至返回的过程中,以下哪些阶段返回舱的机械能守恒
A. 飞船升空的阶段 B. 飞船在椭圆轨道上绕地球运行的阶段 C. 返回舱在大气层外向着地球做无动力飞行阶段 D. 降落伞张开后,返回舱下降的阶段
B、C
