人教版(2019)必修第二册 第七章 全章复习课件 (共34张PPT)
文档属性
| 名称 | 人教版(2019)必修第二册 第七章 全章复习课件 (共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-28 18:10:38 | ||
图片预览






文档简介
(共34张PPT)
第七章 全章复习
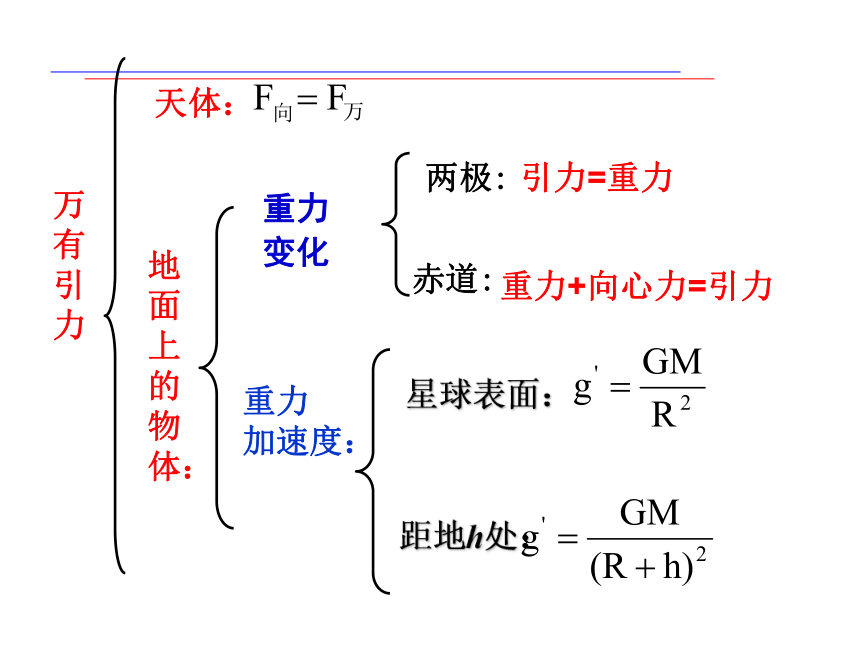
万有引力
天体:
地面上的物体:
重力
变化
两极:
引力=重力
赤道:
重力+向心力=引力
距地h处:
星球表面:
重力
加速度:
一.开普勒三定律
1.开普勒第一定律:
太阳
轨道定律:所有行星绕太阳做椭圆运动,太阳在椭圆的一个焦点上
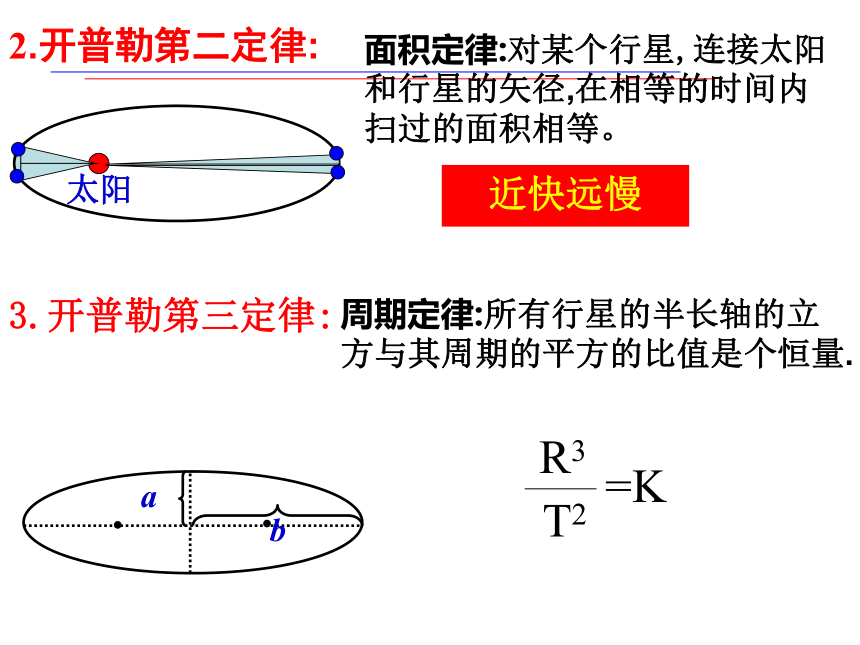
2.开普勒第二定律:
太阳
面积定律:对某个行星,连接太阳和行星的矢径,在相等的时间内扫过的面积相等。
3.开普勒第三定律:
b
a
周期定律:所有行星的半长轴的立方与其周期的平方的比值是个恒量.
近快远慢
R3
T2
=K
1、寻找开普勒第三定律中的K
设某行星绕太阳做匀速圆周运动,其轨道半径为r,周期为T,太阳质量为M,请确定衡量K。
【结论】K只与中心被绕天体(M)有关。
2、一个太空探测器进入一个圆形轨道绕太阳运转,已知其轨道半径为地球绕太阳运转轨道半径的9倍,则太空探测器绕太阳运转的周期是【 】
A.9年 B.3年 C.27年 D.81年
C
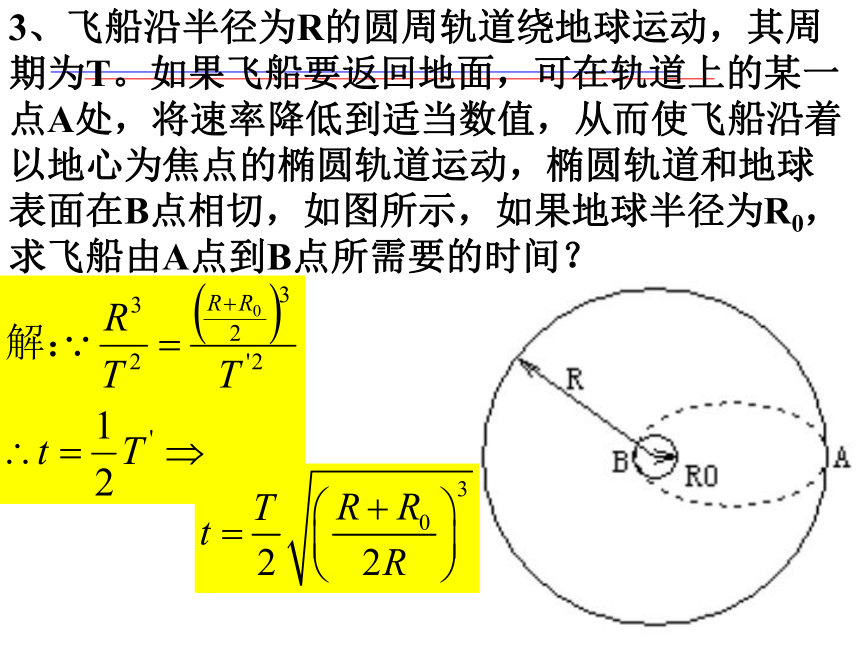
3、飞船沿半径为R的圆周轨道绕地球运动,其周期为T。如果飞船要返回地面,可在轨道上的某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的椭圆轨道运动,椭圆轨道和地球表面在B点相切,如图所示,如果地球半径为R0,求飞船由A点到B点所需要的时间?
二、万有引力定律
2、公式表示:
3、(1)G是引力常量,适用于任何两个物体;它在数值上等于两个质量都是1kg的物体相距1m时的相互作用力.
(2)r是两物体之间的距离,当两物体是质量均匀分布的球体时,r是指两球心间距离;
自然界中任何两个物体都相互吸引,引力的方向在他们的连线上, 引力的大小与两物体的质量M和m的乘 积成正比,与它们之间距离r的二次方成反比。
1、内容:
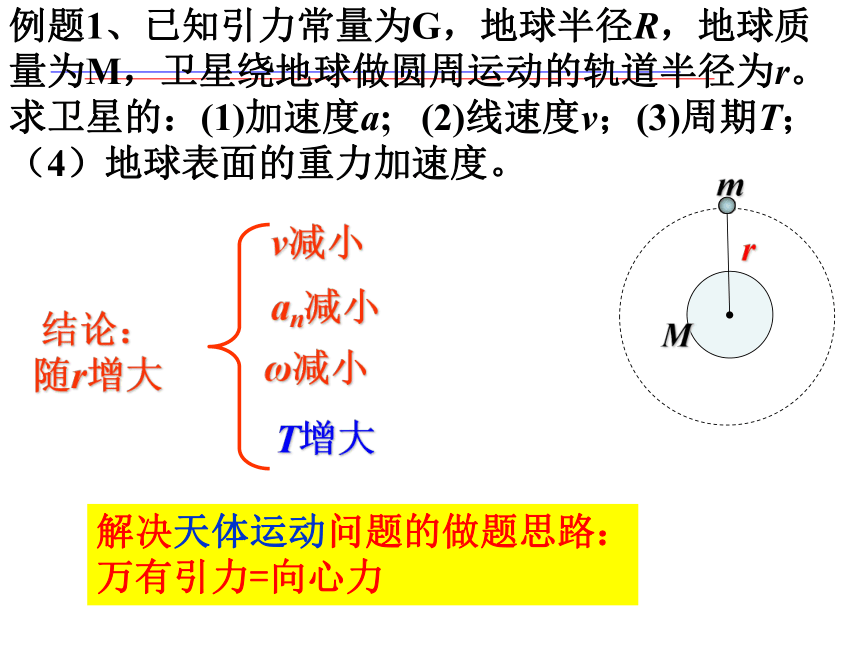
例题1、已知引力常量为G,地球半径R,地球质量为M,卫星绕地球做圆周运动的轨道半径为r。 求卫星的:(1)加速度a; (2)线速度v;(3)周期T;(4)地球表面的重力加速度。
解决天体运动问题的做题思路:
万有引力=向心力
r
M
m
an减小
ω减小
T增大
v减小
结论: 随r增大
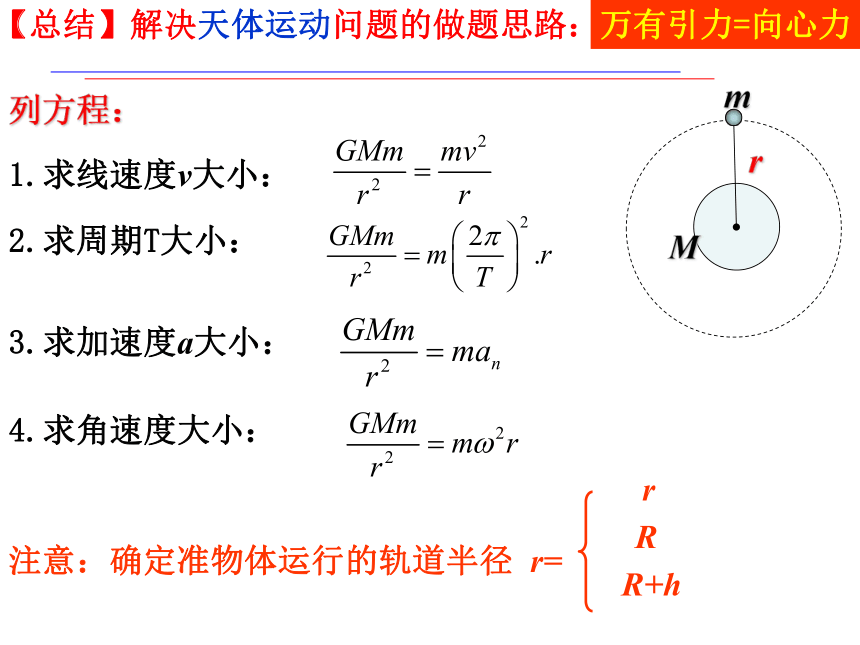
【总结】解决天体运动问题的做题思路:
r
M
m
列方程:
1.求线速度v大小:
2.求周期T大小:
3.求加速度a大小:
4.求角速度大小:
注意:确定准物体运行的轨道半径 r=
r
R+h
R
万有引力=向心力
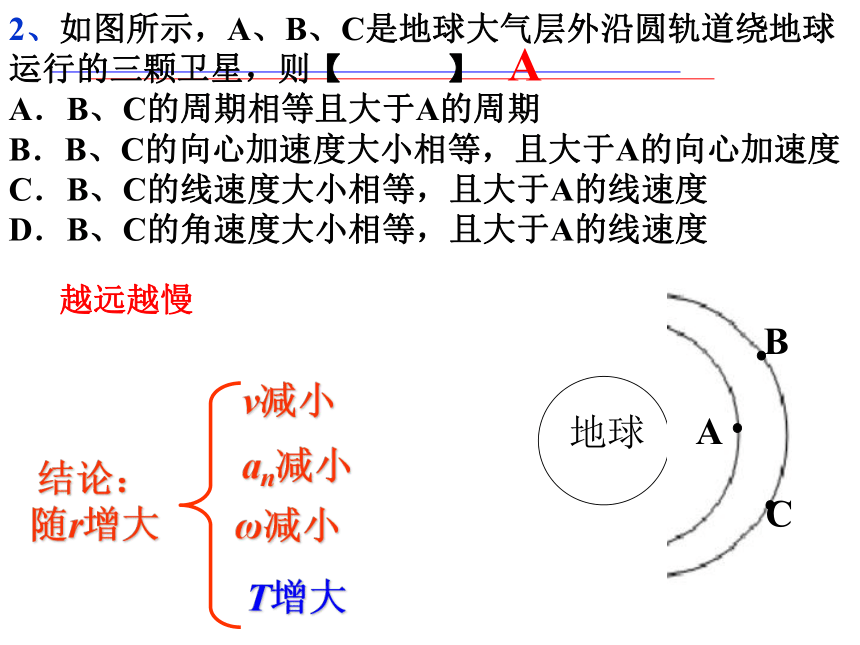
2、如图所示,A、B、C是地球大气层外沿圆轨道绕地球运行的三颗卫星,则【 】
A.B、C的周期相等且大于A的周期
B.B、C的向心加速度大小相等,且大于A的向心加速度
C.B、C的线速度大小相等,且大于A的线速度
D.B、C的角速度大小相等,且大于A的线速度
an减小
ω减小
T增大
v减小
结论: 随r增大
地球
A
B
C
A
越远越慢
图13
3、(09春) 2008年9月27日,“神舟七号”航天员翟志刚首次实现了中国航天员在太空的舱外活动(图13),这是我国航天发展史上的又一里程碑。已知引力常量为G,地球质量为M,地球半径为R。飞船绕地球做匀速圆周运动的过程中,距地面的高度为h,求:
(1)飞船加速度a的大小;
(2)飞船速度v的大小。
预定圆
轨道
图15
5、(10夏) 2008年9月25日21时10分,我国成功发射了神舟七号飞船。用长征二号F型运载火箭将神舟七号送入椭圆轨道,实施变轨后,再进入预定圆轨道,如图15所示。飞船在预定圆轨道上飞行n圈所用时间为t,地球的质量为M,地球半径为R,万有引力常量为G,求:
(1)飞船在预定圆轨道上飞行的周期T;
(2)飞船在预定圆轨道上飞行速度v的大小。
1、已知地球的半径R, 地球表面的重力加速度g, 环绕地球表面做圆周运动的卫星的速度为v,万有引力常量为G,求地球的质量和密度。
2、若月球围绕地球做匀速圆周运动,其周期为T,又知月球到地心的距离为r,地球半径为R,试求出地球的质量和密度。
【解】万有引力提供月球做圆周运动的向心力:
2.测出天体的半径R和表面的重力加速度g
三、万有引力的应用--天体质量或密度的估算
1. 测出卫星围绕天体做匀速圆周运动的周期T
【总结】万有引力与重力的区别
(一)地球表面上物体的重量变化
1.两极:
引力=重力.
2.赤道:
重力+向心力=引力.
3.重力的变化:
随纬度的增大而增大
(二)卫星的重力就是引力
F引
G
G
F引
F向
练习1、2007年10月24日,我国“嫦娥一号”探月卫星成功发射。“嫦娥一号”卫星开始绕地球做椭圆轨道运动,经过变轨、制动后,成为一颗绕月球做圆轨道运动的卫星。设卫星距月球表面的高度为h,已知月球半径为R,质量为M,引力常量为G。求:
(1)月球表面的重力加速度g;
(2)卫星所在处的重力加速度g’;
解:(1)月球表面:
(2)距离地面h处:
.
.
.
.
.
.
.
.
.
.
.
练习3、地球半径为R,地球表面的重力加速度为g,若高空中某处的重力加速度为g/4,则该处距地面球表面的高度h为
练习4、一名宇航员抵达一半径为R的星球表面后,为了测定该星球的质量,做了如下实验:将一个小球从该星球表面某位置以初速度v竖直向上抛出,小球在空中运动一段时间后又落回原抛出位置,测得小球在空中运动的时间为t,已知万有引力恒量为G,不计阻力。试根据题中所提供的条件和测量结果,求:
(1)该星球表面的“重力”加速度g的大小;
(2)该星球的质量M;
(3)如果在该星球上发射一颗围绕该星球做匀速圆周运动的卫星,则该卫星运行的最小周期T为多大?
5、某行星的自转周期为T=6h,用弹簧秤在该行星的”赤道“和”两极“处测同一物体的重力,在该星球的赤道测得的读数为在其北极所得读数的90%, (星球视为球体)。求该行星的平均密度是多大?
10%的引力到哪去了?
卫星的轨道圆心在哪儿?
所有卫星的轨道圆心都在地心上。
人造卫星 宇宙速度
(一)宇宙速度
1、第一宇宙速度(环绕速度)v1=7.9km/s.
它等于近地卫星绕地球表面做匀速圆周运动的线速度.
它是从地面成功发射一个卫星的最小发射速度!
2、第二宇宙速度(脱离速度) v2=11.2 km/s
这是卫星挣脱地球的引力束缚,成为绕太阳运行的人造行星的最小发射速度.
3、第三宇宙速度(逃逸速度)v3=16.7 km/s
这是卫星挣脱太阳引力束缚的最小发射速度.
1、近地卫星
F万
在地球表面处飞行的卫星,但是已经脱离地表了!
(1)作圆周运动的轨道半径为地球半径R;
(2)由于紧贴地表,卫星的重力加速度为g。
(二)人造卫星
它·绕地球表面做匀速圆周运动的线速度最大!!
2、地球同步卫星
(1)相对于地面静止的和地球具有相同周期的卫星.
(2)同步卫星的特点:
①周期T=24h
②离地球表面高度一定h=36000km
③必须在赤道上空
人造卫星
近地
卫星
R
T=85min
T=24h
在赤道上空,h=36000km
同步
卫星:
v=7.9km/s
【练一练】通信卫星又叫同步卫星,下面关于同步卫星的说法中正确的是 【 】
A.所有的地球同步卫星都位于地球的赤道平面内
B.所有的地球同步卫星的质量都相等
C.所有的地球同步卫星绕地球作匀速圆周运动的
角速度都相等
D.所有的地球同步卫星离地球的高度都相等
ACD
【练一练】据报道,我国首颗数据中继卫星----“天链一号01星”,于2008.4.25在西昌卫星发射中心成功发射,经过四次变轨控制后,于5.1成功定点在东京770赤道上空的同步轨道,关于成功定点“天链一号01星”说法正确的是【 】
A.运行速度大于7.9km/s
B.离地面高度一定,相对地面静止
C.绕地球运行的角速度比月球运行的角速度大
D.向心加速度比静止在赤道上的物体的向心加速度小
BC
【神奇的双星】:
在宇宙中,恒星有单个的,例如我们所在的太阳系中的太阳;有两个恒星相伴的;也有多个恒星聚会的,花样十分丰富.据观测:每四颗星中只有一颗是单独行动的,其它大概有三分之一是双星,我们把两颗相伴在一起的彼此紧密环绕而行的恒星称为双星(Binary Stars),例如仙王U变星.而其余的则是多星聚星,例如巨蟹座三合星.所有这些结群的星在肉眼看来都是单独的,多数即使用望远镜看来也象是单独的,贴得最近的星只有用摄谱仪才能探测出来.
仙王U变星
巨蟹座三合星
L
m1
m2
r2
r1
1.向心力大小相等:
2.周期和角速度相等:
七、双星问题:靠两颗星球间的引力,提供各自所需要的向心力的星球称为双星。
3.轨道半径的关系:
它们的轨道半径与质量成反比。
八、发射地球同步卫星的过程:
1、先成为近地卫星,进入圆形轨道(近地轨道);
2、在A点二次点火加速,进入椭圆轨道;
3、在B点再次加速进入圆形轨道(远地轨道)。
3
B
2
A
1
1、发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行.最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,则当卫星分别在1,2,3轨道上正常运行时以下说法对的是【 】
A.卫星在轨道3上的速率大于在轨道1上的速率.
B.卫星在轨道3上的角速度小于在轨道1上的角速度.
C.卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点的加速度.
D.卫星在轨道2上经过P点时的速度小于它在轨道3上经过P点时的速度.
P
Q
1
2
3
BD
离心条件
【总结】变轨问题
P
Q
3
1
2
图8
(1)匀速圆周运动相比就用F引=F向做; (2)椭圆轨道与圆周运动相比用离心和向心来做。
第七章 全章复习
万有引力
天体:
地面上的物体:
重力
变化
两极:
引力=重力
赤道:
重力+向心力=引力
距地h处:
星球表面:
重力
加速度:
一.开普勒三定律
1.开普勒第一定律:
太阳
轨道定律:所有行星绕太阳做椭圆运动,太阳在椭圆的一个焦点上
2.开普勒第二定律:
太阳
面积定律:对某个行星,连接太阳和行星的矢径,在相等的时间内扫过的面积相等。
3.开普勒第三定律:
b
a
周期定律:所有行星的半长轴的立方与其周期的平方的比值是个恒量.
近快远慢
R3
T2
=K
1、寻找开普勒第三定律中的K
设某行星绕太阳做匀速圆周运动,其轨道半径为r,周期为T,太阳质量为M,请确定衡量K。
【结论】K只与中心被绕天体(M)有关。
2、一个太空探测器进入一个圆形轨道绕太阳运转,已知其轨道半径为地球绕太阳运转轨道半径的9倍,则太空探测器绕太阳运转的周期是【 】
A.9年 B.3年 C.27年 D.81年
C
3、飞船沿半径为R的圆周轨道绕地球运动,其周期为T。如果飞船要返回地面,可在轨道上的某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的椭圆轨道运动,椭圆轨道和地球表面在B点相切,如图所示,如果地球半径为R0,求飞船由A点到B点所需要的时间?
二、万有引力定律
2、公式表示:
3、(1)G是引力常量,适用于任何两个物体;它在数值上等于两个质量都是1kg的物体相距1m时的相互作用力.
(2)r是两物体之间的距离,当两物体是质量均匀分布的球体时,r是指两球心间距离;
自然界中任何两个物体都相互吸引,引力的方向在他们的连线上, 引力的大小与两物体的质量M和m的乘 积成正比,与它们之间距离r的二次方成反比。
1、内容:
例题1、已知引力常量为G,地球半径R,地球质量为M,卫星绕地球做圆周运动的轨道半径为r。 求卫星的:(1)加速度a; (2)线速度v;(3)周期T;(4)地球表面的重力加速度。
解决天体运动问题的做题思路:
万有引力=向心力
r
M
m
an减小
ω减小
T增大
v减小
结论: 随r增大
【总结】解决天体运动问题的做题思路:
r
M
m
列方程:
1.求线速度v大小:
2.求周期T大小:
3.求加速度a大小:
4.求角速度大小:
注意:确定准物体运行的轨道半径 r=
r
R+h
R
万有引力=向心力
2、如图所示,A、B、C是地球大气层外沿圆轨道绕地球运行的三颗卫星,则【 】
A.B、C的周期相等且大于A的周期
B.B、C的向心加速度大小相等,且大于A的向心加速度
C.B、C的线速度大小相等,且大于A的线速度
D.B、C的角速度大小相等,且大于A的线速度
an减小
ω减小
T增大
v减小
结论: 随r增大
地球
A
B
C
A
越远越慢
图13
3、(09春) 2008年9月27日,“神舟七号”航天员翟志刚首次实现了中国航天员在太空的舱外活动(图13),这是我国航天发展史上的又一里程碑。已知引力常量为G,地球质量为M,地球半径为R。飞船绕地球做匀速圆周运动的过程中,距地面的高度为h,求:
(1)飞船加速度a的大小;
(2)飞船速度v的大小。
预定圆
轨道
图15
5、(10夏) 2008年9月25日21时10分,我国成功发射了神舟七号飞船。用长征二号F型运载火箭将神舟七号送入椭圆轨道,实施变轨后,再进入预定圆轨道,如图15所示。飞船在预定圆轨道上飞行n圈所用时间为t,地球的质量为M,地球半径为R,万有引力常量为G,求:
(1)飞船在预定圆轨道上飞行的周期T;
(2)飞船在预定圆轨道上飞行速度v的大小。
1、已知地球的半径R, 地球表面的重力加速度g, 环绕地球表面做圆周运动的卫星的速度为v,万有引力常量为G,求地球的质量和密度。
2、若月球围绕地球做匀速圆周运动,其周期为T,又知月球到地心的距离为r,地球半径为R,试求出地球的质量和密度。
【解】万有引力提供月球做圆周运动的向心力:
2.测出天体的半径R和表面的重力加速度g
三、万有引力的应用--天体质量或密度的估算
1. 测出卫星围绕天体做匀速圆周运动的周期T
【总结】万有引力与重力的区别
(一)地球表面上物体的重量变化
1.两极:
引力=重力.
2.赤道:
重力+向心力=引力.
3.重力的变化:
随纬度的增大而增大
(二)卫星的重力就是引力
F引
G
G
F引
F向
练习1、2007年10月24日,我国“嫦娥一号”探月卫星成功发射。“嫦娥一号”卫星开始绕地球做椭圆轨道运动,经过变轨、制动后,成为一颗绕月球做圆轨道运动的卫星。设卫星距月球表面的高度为h,已知月球半径为R,质量为M,引力常量为G。求:
(1)月球表面的重力加速度g;
(2)卫星所在处的重力加速度g’;
解:(1)月球表面:
(2)距离地面h处:
.
.
.
.
.
.
.
.
.
.
.
练习3、地球半径为R,地球表面的重力加速度为g,若高空中某处的重力加速度为g/4,则该处距地面球表面的高度h为
练习4、一名宇航员抵达一半径为R的星球表面后,为了测定该星球的质量,做了如下实验:将一个小球从该星球表面某位置以初速度v竖直向上抛出,小球在空中运动一段时间后又落回原抛出位置,测得小球在空中运动的时间为t,已知万有引力恒量为G,不计阻力。试根据题中所提供的条件和测量结果,求:
(1)该星球表面的“重力”加速度g的大小;
(2)该星球的质量M;
(3)如果在该星球上发射一颗围绕该星球做匀速圆周运动的卫星,则该卫星运行的最小周期T为多大?
5、某行星的自转周期为T=6h,用弹簧秤在该行星的”赤道“和”两极“处测同一物体的重力,在该星球的赤道测得的读数为在其北极所得读数的90%, (星球视为球体)。求该行星的平均密度是多大?
10%的引力到哪去了?
卫星的轨道圆心在哪儿?
所有卫星的轨道圆心都在地心上。
人造卫星 宇宙速度
(一)宇宙速度
1、第一宇宙速度(环绕速度)v1=7.9km/s.
它等于近地卫星绕地球表面做匀速圆周运动的线速度.
它是从地面成功发射一个卫星的最小发射速度!
2、第二宇宙速度(脱离速度) v2=11.2 km/s
这是卫星挣脱地球的引力束缚,成为绕太阳运行的人造行星的最小发射速度.
3、第三宇宙速度(逃逸速度)v3=16.7 km/s
这是卫星挣脱太阳引力束缚的最小发射速度.
1、近地卫星
F万
在地球表面处飞行的卫星,但是已经脱离地表了!
(1)作圆周运动的轨道半径为地球半径R;
(2)由于紧贴地表,卫星的重力加速度为g。
(二)人造卫星
它·绕地球表面做匀速圆周运动的线速度最大!!
2、地球同步卫星
(1)相对于地面静止的和地球具有相同周期的卫星.
(2)同步卫星的特点:
①周期T=24h
②离地球表面高度一定h=36000km
③必须在赤道上空
人造卫星
近地
卫星
R
T=85min
T=24h
在赤道上空,h=36000km
同步
卫星:
v=7.9km/s
【练一练】通信卫星又叫同步卫星,下面关于同步卫星的说法中正确的是 【 】
A.所有的地球同步卫星都位于地球的赤道平面内
B.所有的地球同步卫星的质量都相等
C.所有的地球同步卫星绕地球作匀速圆周运动的
角速度都相等
D.所有的地球同步卫星离地球的高度都相等
ACD
【练一练】据报道,我国首颗数据中继卫星----“天链一号01星”,于2008.4.25在西昌卫星发射中心成功发射,经过四次变轨控制后,于5.1成功定点在东京770赤道上空的同步轨道,关于成功定点“天链一号01星”说法正确的是【 】
A.运行速度大于7.9km/s
B.离地面高度一定,相对地面静止
C.绕地球运行的角速度比月球运行的角速度大
D.向心加速度比静止在赤道上的物体的向心加速度小
BC
【神奇的双星】:
在宇宙中,恒星有单个的,例如我们所在的太阳系中的太阳;有两个恒星相伴的;也有多个恒星聚会的,花样十分丰富.据观测:每四颗星中只有一颗是单独行动的,其它大概有三分之一是双星,我们把两颗相伴在一起的彼此紧密环绕而行的恒星称为双星(Binary Stars),例如仙王U变星.而其余的则是多星聚星,例如巨蟹座三合星.所有这些结群的星在肉眼看来都是单独的,多数即使用望远镜看来也象是单独的,贴得最近的星只有用摄谱仪才能探测出来.
仙王U变星
巨蟹座三合星
L
m1
m2
r2
r1
1.向心力大小相等:
2.周期和角速度相等:
七、双星问题:靠两颗星球间的引力,提供各自所需要的向心力的星球称为双星。
3.轨道半径的关系:
它们的轨道半径与质量成反比。
八、发射地球同步卫星的过程:
1、先成为近地卫星,进入圆形轨道(近地轨道);
2、在A点二次点火加速,进入椭圆轨道;
3、在B点再次加速进入圆形轨道(远地轨道)。
3
B
2
A
1
1、发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行.最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,则当卫星分别在1,2,3轨道上正常运行时以下说法对的是【 】
A.卫星在轨道3上的速率大于在轨道1上的速率.
B.卫星在轨道3上的角速度小于在轨道1上的角速度.
C.卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点的加速度.
D.卫星在轨道2上经过P点时的速度小于它在轨道3上经过P点时的速度.
P
Q
1
2
3
BD
离心条件
【总结】变轨问题
P
Q
3
1
2
图8
(1)匀速圆周运动相比就用F引=F向做; (2)椭圆轨道与圆周运动相比用离心和向心来做。
