人教版小学数学五年级上册6.4《组合图形的面积》同步练习(含答案)
文档属性
| 名称 | 人教版小学数学五年级上册6.4《组合图形的面积》同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 180.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 00:00:00 | ||
图片预览

文档简介
6.4 组合图形的面积 同步练习
一、单选题
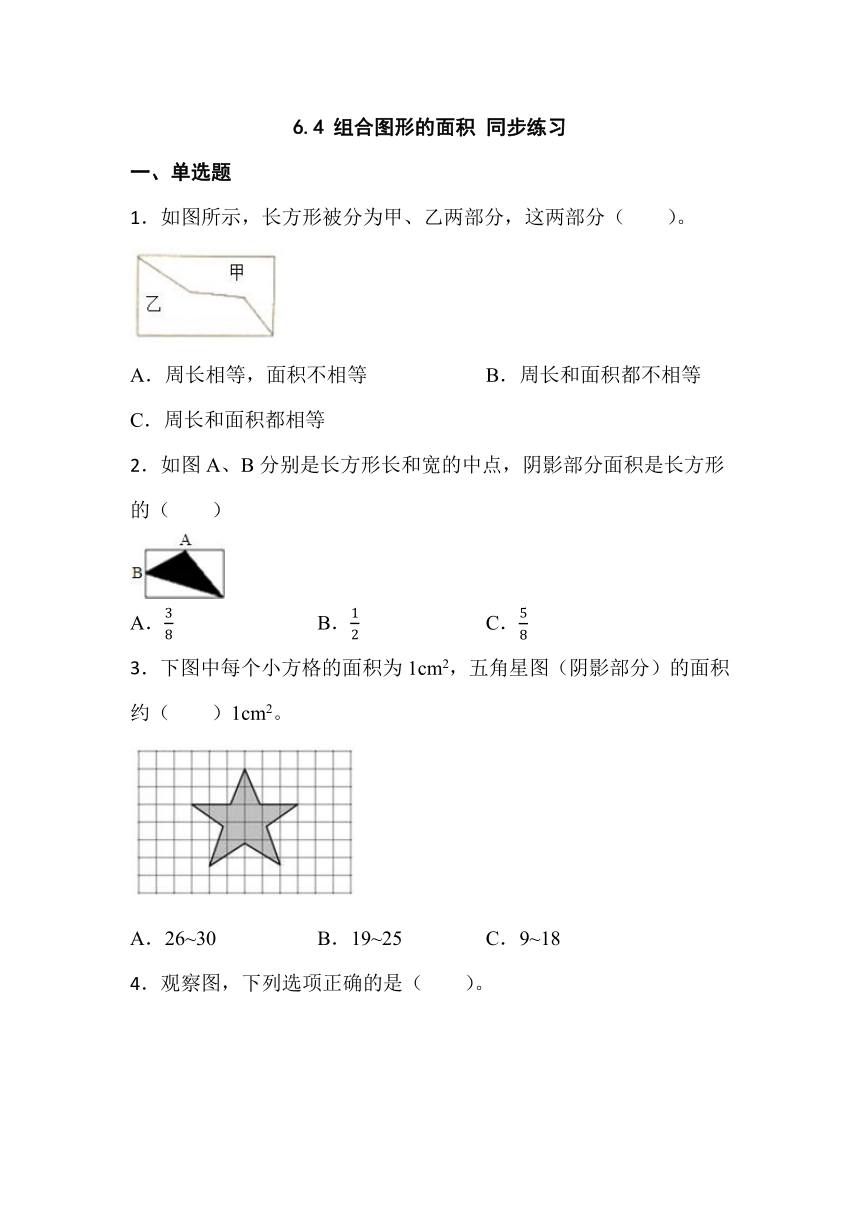
1.如图所示,长方形被分为甲、乙两部分,这两部分( )。
A.周长相等,面积不相等 B.周长和面积都不相等
C.周长和面积都相等
2.如图A、B分别是长方形长和宽的中点,阴影部分面积是长方形的( )
A. B. C.
3.下图中每个小方格的面积为1cm2,五角星图(阴影部分)的面积约( )1cm2。
A.26~30 B.19~25 C.9~18
4.观察图,下列选项正确的是( )。
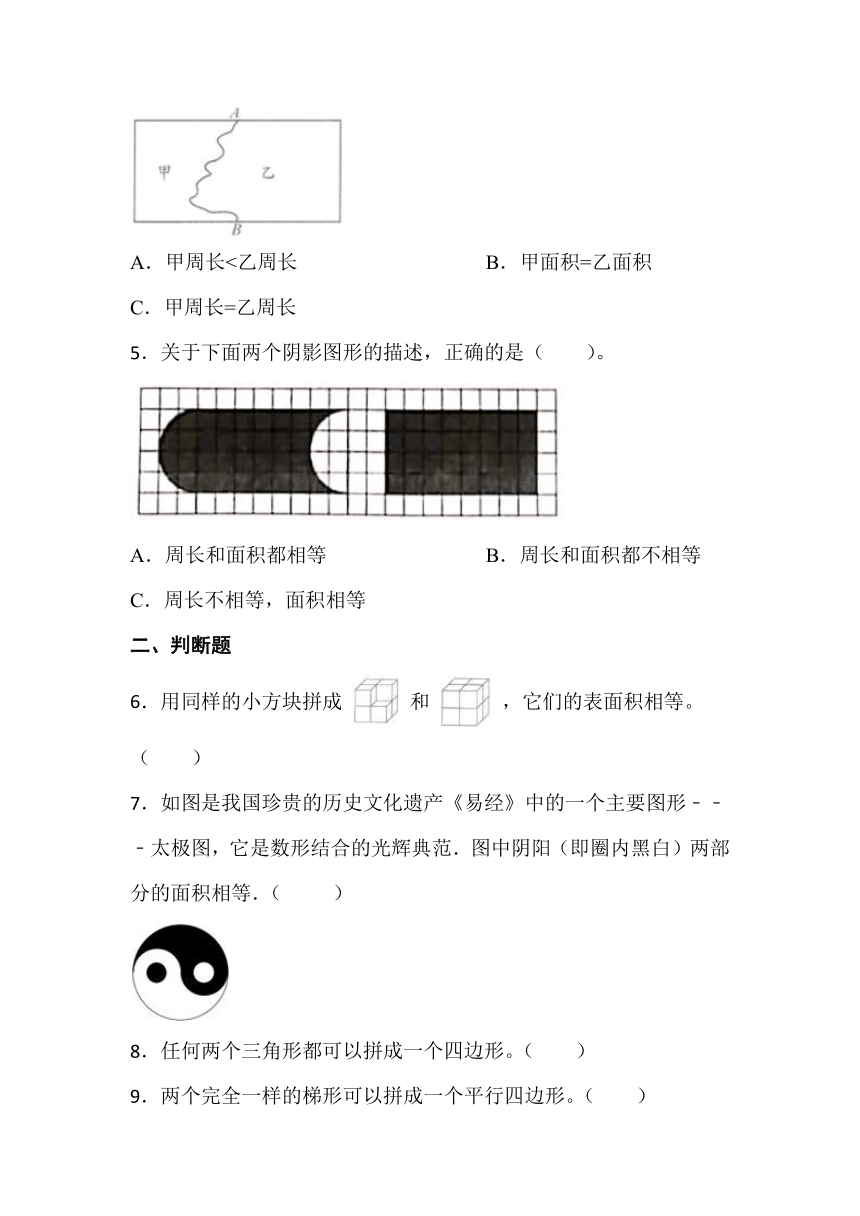
A.甲周长<乙周长 B.甲面积=乙面积
C.甲周长=乙周长
5.关于下面两个阴影图形的描述,正确的是( )。
A.周长和面积都相等 B.周长和面积都不相等
C.周长不相等,面积相等
二、判断题
6.用同样的小方块拼成 和 ,它们的表面积相等。( )
7.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.( )
8.任何两个三角形都可以拼成一个四边形。( )
9.两个完全一样的梯形可以拼成一个平行四边形。( )
10.面积相等的图形,形状一定相同.( )
三、填空题
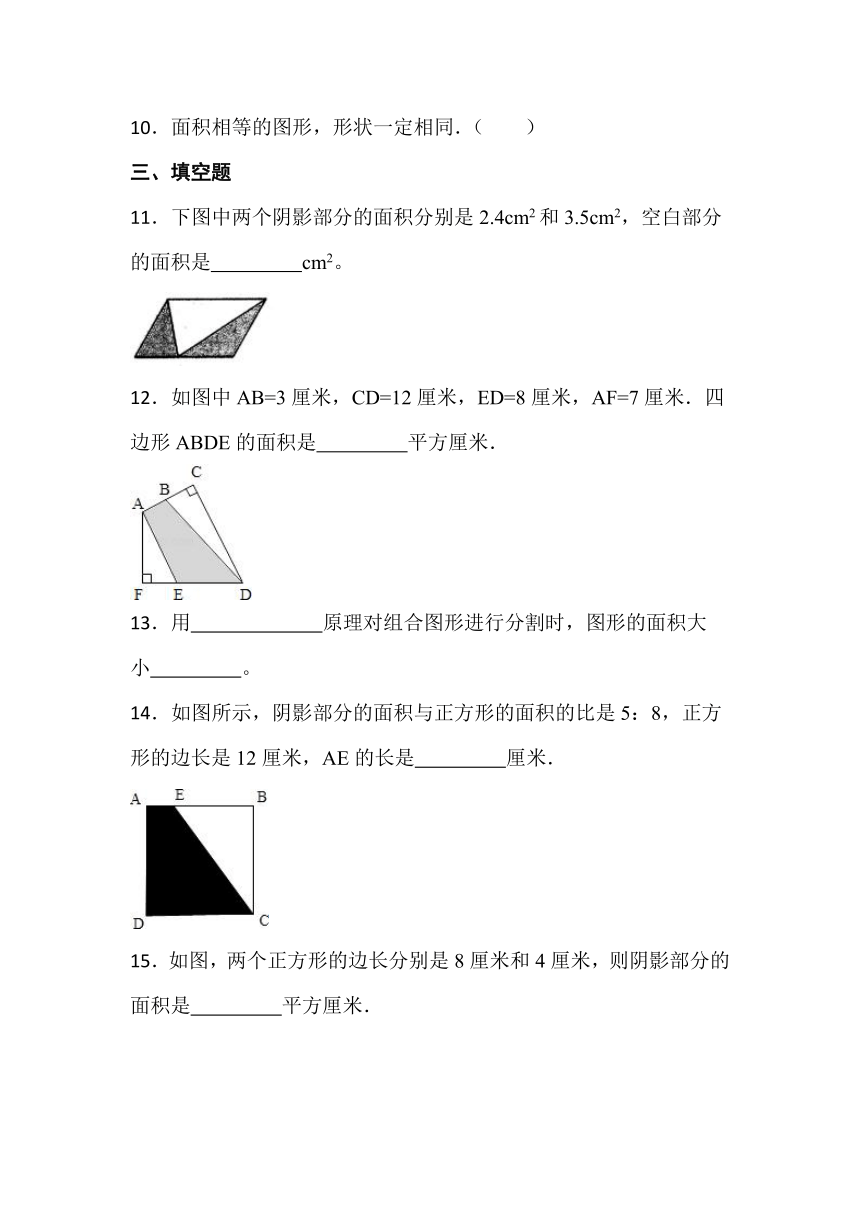
11.下图中两个阴影部分的面积分别是2.4cm2和3.5cm2,空白部分的面积是 cm2。
12.如图中AB=3厘米,CD=12厘米,ED=8厘米,AF=7厘米.四边形ABDE的面积是 平方厘米.
13.用 原理对组合图形进行分割时,图形的面积大小 。
14.如图所示,阴影部分的面积与正方形的面积的比是5:8,正方形的边长是12厘米,AE的长是 厘米.
15.如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是 平方厘米.
四、计算题
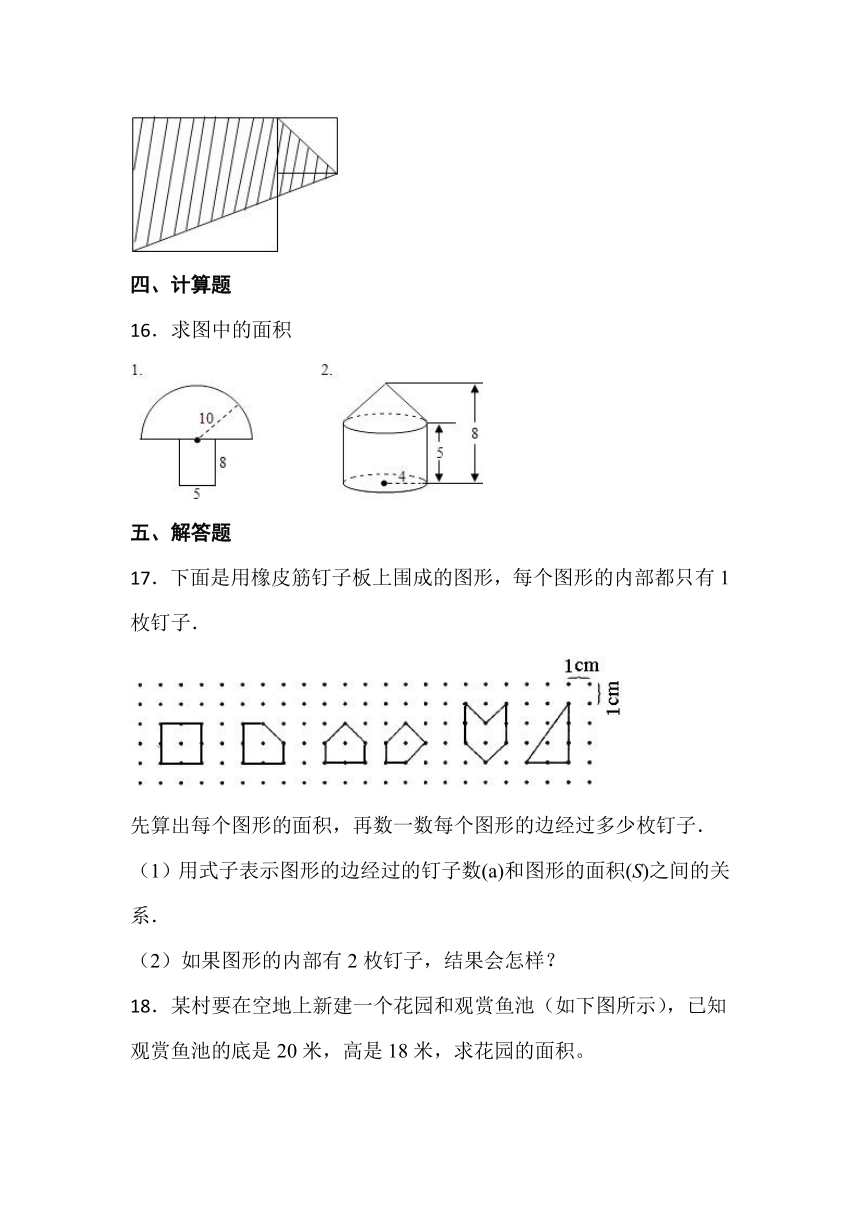
16.求图中的面积
五、解答题
17.下面是用橡皮筋钉子板上围成的图形,每个图形的内部都只有1枚钉子.
先算出每个图形的面积,再数一数每个图形的边经过多少枚钉子.
(1)用式子表示图形的边经过的钉子数(a)和图形的面积(S)之间的关系.
(2)如果图形的内部有2枚钉子,结果会怎样?
18.某村要在空地上新建一个花园和观赏鱼池(如下图所示),已知观赏鱼池的底是20米,高是18米,求花园的面积。
19.下图是一个平行四边形和一个阴影三角形组合成的梯形,梯形面积是25平方厘米,求阴影三角形面积。单位:cm
参考答案
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】正确
7.【答案】正确
8.【答案】错误
9.【答案】正确
10.【答案】错误
11.【答案】5.9
12.【答案】46
13.【答案】出入相补;不变
14.【答案】3
15.【答案】64
16.【答案】解:①3.14×102÷2+8×5,
=314÷2+40,
=157+40,
=197;
答:组合图形的面积是197
② ×3.14×42×(8﹣5)+3.14×42×5,
=3.14×16+3.14×16×5,
=50.24+251.2,
=301.44;
答:这个组合体的体积是301.44
17.【答案】(1)解:第一个,面积:2×2=4(平方厘米),经过的钉子数是8;
第二个,面积:3.5平方厘米,经过的钉子数是7;
第三个,面积:3平方厘米,经过的钉子数是6;
第四个,面积:2.5平方厘米,经过的钉子数是5;
第五个,面积:4平方厘米,经过的钉子数是8;
第六个,面积:3平方厘米,经过的钉子数是6;
面积是钉子个数的一半,用式子表示是:S=a÷2.
(2)解:S=a÷2+1
18.【答案】解:(50+60)×36÷2
=110×36÷2
=3960÷2
=1980(平方米)
20×18÷2
=360÷2
=180(平方米)
1980-180=1800(平方米)
答:花园的面积是1800平方米。
19.【答案】解:梯形的高即三角形的高:h=25×2÷(3+7)=5cm
阴影三角形面积:(7-3)×5÷2=10cm2
答:阴影三角形面积是10cm2
一、单选题
1.如图所示,长方形被分为甲、乙两部分,这两部分( )。
A.周长相等,面积不相等 B.周长和面积都不相等
C.周长和面积都相等
2.如图A、B分别是长方形长和宽的中点,阴影部分面积是长方形的( )
A. B. C.
3.下图中每个小方格的面积为1cm2,五角星图(阴影部分)的面积约( )1cm2。
A.26~30 B.19~25 C.9~18
4.观察图,下列选项正确的是( )。
A.甲周长<乙周长 B.甲面积=乙面积
C.甲周长=乙周长
5.关于下面两个阴影图形的描述,正确的是( )。
A.周长和面积都相等 B.周长和面积都不相等
C.周长不相等,面积相等
二、判断题
6.用同样的小方块拼成 和 ,它们的表面积相等。( )
7.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.( )
8.任何两个三角形都可以拼成一个四边形。( )
9.两个完全一样的梯形可以拼成一个平行四边形。( )
10.面积相等的图形,形状一定相同.( )
三、填空题
11.下图中两个阴影部分的面积分别是2.4cm2和3.5cm2,空白部分的面积是 cm2。
12.如图中AB=3厘米,CD=12厘米,ED=8厘米,AF=7厘米.四边形ABDE的面积是 平方厘米.
13.用 原理对组合图形进行分割时,图形的面积大小 。
14.如图所示,阴影部分的面积与正方形的面积的比是5:8,正方形的边长是12厘米,AE的长是 厘米.
15.如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是 平方厘米.
四、计算题
16.求图中的面积
五、解答题
17.下面是用橡皮筋钉子板上围成的图形,每个图形的内部都只有1枚钉子.
先算出每个图形的面积,再数一数每个图形的边经过多少枚钉子.
(1)用式子表示图形的边经过的钉子数(a)和图形的面积(S)之间的关系.
(2)如果图形的内部有2枚钉子,结果会怎样?
18.某村要在空地上新建一个花园和观赏鱼池(如下图所示),已知观赏鱼池的底是20米,高是18米,求花园的面积。
19.下图是一个平行四边形和一个阴影三角形组合成的梯形,梯形面积是25平方厘米,求阴影三角形面积。单位:cm
参考答案
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】正确
7.【答案】正确
8.【答案】错误
9.【答案】正确
10.【答案】错误
11.【答案】5.9
12.【答案】46
13.【答案】出入相补;不变
14.【答案】3
15.【答案】64
16.【答案】解:①3.14×102÷2+8×5,
=314÷2+40,
=157+40,
=197;
答:组合图形的面积是197
② ×3.14×42×(8﹣5)+3.14×42×5,
=3.14×16+3.14×16×5,
=50.24+251.2,
=301.44;
答:这个组合体的体积是301.44
17.【答案】(1)解:第一个,面积:2×2=4(平方厘米),经过的钉子数是8;
第二个,面积:3.5平方厘米,经过的钉子数是7;
第三个,面积:3平方厘米,经过的钉子数是6;
第四个,面积:2.5平方厘米,经过的钉子数是5;
第五个,面积:4平方厘米,经过的钉子数是8;
第六个,面积:3平方厘米,经过的钉子数是6;
面积是钉子个数的一半,用式子表示是:S=a÷2.
(2)解:S=a÷2+1
18.【答案】解:(50+60)×36÷2
=110×36÷2
=3960÷2
=1980(平方米)
20×18÷2
=360÷2
=180(平方米)
1980-180=1800(平方米)
答:花园的面积是1800平方米。
19.【答案】解:梯形的高即三角形的高:h=25×2÷(3+7)=5cm
阴影三角形面积:(7-3)×5÷2=10cm2
答:阴影三角形面积是10cm2
