24.3.4相似三角形的运用(广东省佛山市顺德区)
文档属性
| 名称 | 24.3.4相似三角形的运用(广东省佛山市顺德区) |

|
|
| 格式 | rar | ||
| 文件大小 | 321.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-01 00:00:00 | ||
图片预览




文档简介
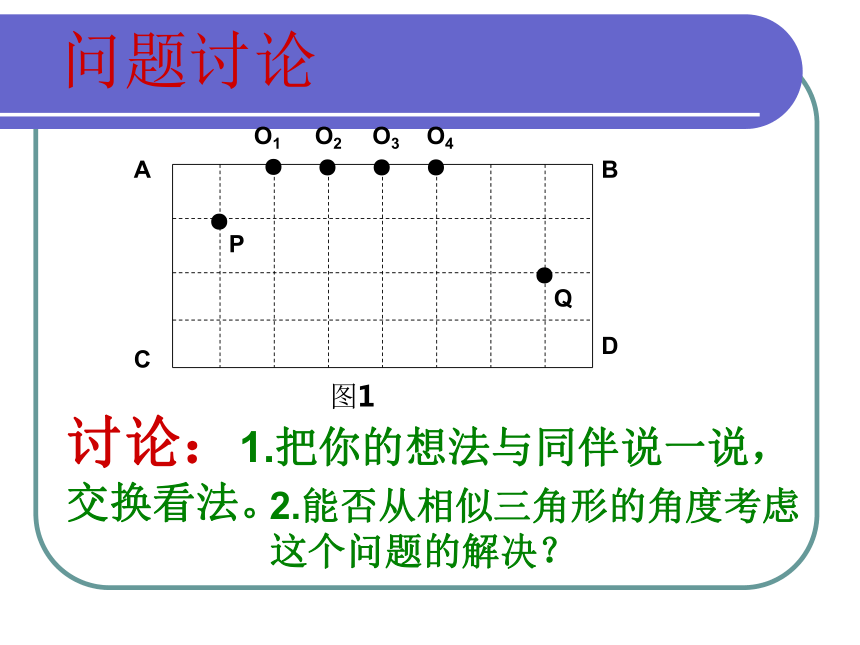
课件17张PPT。24.3.4相似三角形的应用创设情境 引入新课2005年4月3日,台球“神童”丁俊辉夺得世界职业台球中国公开赛的冠军,书写了世界职业台球历史的新篇章。图1是丁俊辉一次漂亮的击球,P为“母球”,Q为“黑球”,球P经球台的边AB反弹后直接击中黑球Q,则母球P击出时应瞄准AB边上的哪个点?说说你的理由。 ● ● ● ● ● ●ABCDPQO4O3O2O1图1讨论:1.把你的想法与同伴说一说,交换看法。问题讨论2.能否从相似三角形的角度考虑
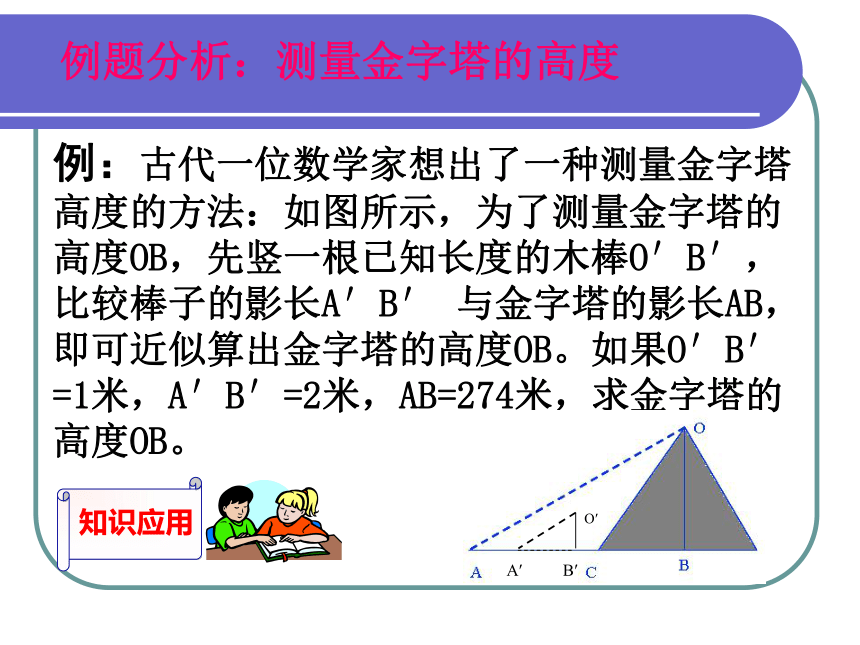
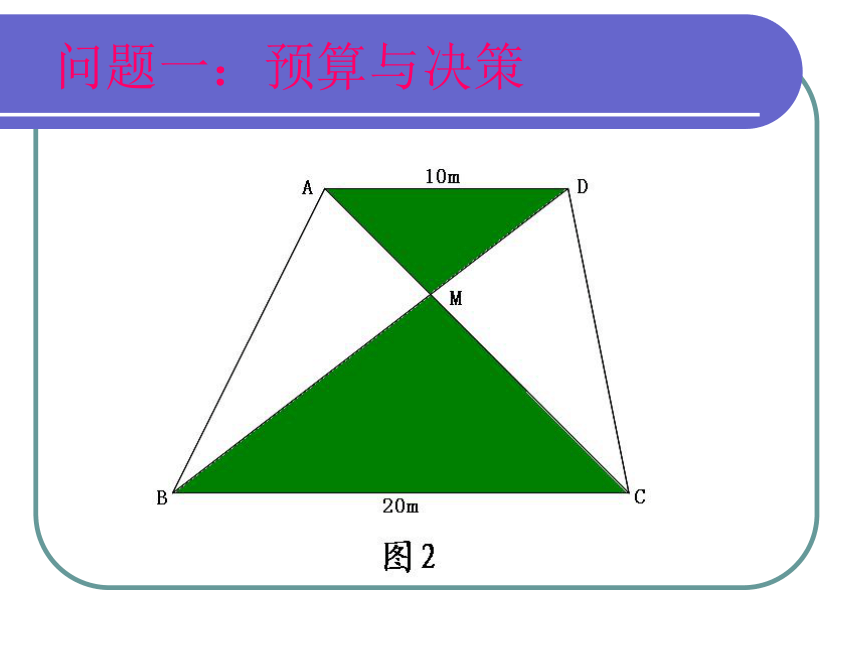
这个问题的解决?教学目标1.本节课总目标是:会利用相似三角形的性质解决简单的实际问题。2.本课时阶段目标是:(1)会直接应用性质解决简单的实际问题;(2)会利用所给的方案构造示意图解决问题;(3)会初步设计解决实际问题的方案;(4)会实地测量和计算旗杆的高度、河的宽度。例题分析:测量金字塔的高度例:古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′ 与金字塔的影长AB,即可近似算出金字塔的高度OB。如果O′B′ =1米,A′B′=2米,AB=274米,求金字塔的高度OB。设置问题,引导研究问题一:预算与决策(应用相似性质解决问题) 某生活小区的居民筹集了1500元,计划在一块上、下底分别为10m、20m的梯形空地上的阴影部分处种植茉莉花,同时在茉莉花的周围小径上铺设健身鹅卵石(如图2)。他们发现:在ΔAMD地带上,种植茉莉花共花了160元,而铺设健身鹅卵石共花了200元,请你预算一下,他们所筹集的资金够用吗? 问题一:预算与决策问题二:测量大运河的宽度: 利用所给的方案构造示意图 大运河的两岸有一段是平行的,为了估算其运河的宽度,我们可以在对岸选定一个目标作为点A,再在运河的这一边选点B、C,使AB⊥BC,然后再选点E,使EC⊥BC,用视线确定BC和AE的交点为D。(1)想象一下,如何确定点的位置?如何画图?(2)要估算运河的宽度,你认为要测量哪些可以测量的线段?ABEDC图3(3)如果测得BD=120m,DC=60m,EC=50m,求出大运河的大致宽度AB。画出图形问题解决问题三:可以这样测量吗? 利用所给的方案构造示意图 河的两岸有一段是平行的,在河的这一岸每隔5m有一棵树,在那河的对岸每隔50m有一根电线杆,在离开岸25m处看对岸测得对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,你能根据以上信息画出示意图,并求出河宽吗? 50 m25 m20 mABCDE问题解决(2)根据题意可知:CD∥AB,AB=50m,CD=20m,DE=25m;设,河宽DE为x m.则EB = (x+25)m . ∵ CD∥AB,∴ΔECD∽ΔEAB. CD∶AB=ED∶EB,解得, x=37.5m.
答:这条河宽约为37.5m问题解决拓展延伸,促进发展问题:能通过这样的测量求出树高吗? 如图,教学楼旁边有一棵树,学习了相似三角形后,数学小组的同学们想利用树影测量树高。课外活动时在阳光下他们测得一根长为1米的竹杆的影长是0.9米,当他们马上测量树的影子长时,发现树的影子不全落在地面上,于是他们测得落在地面上的影子长2.7米,落在墙壁上的影长1.2米。1.2m2.7m拓展延伸,促进发展 如图,在某建筑物4m处有一棵树,在某时刻,1.2m长的竹竿竖直地面,影长为2m,此时,树的影子照射地面,还有一部分影子在建筑物的墙上,墙上的影长为2m,那么这棵树高约为多少m。A′ADCBB′C′课时目标,自我评价本课时的阶段目标是:(1)会直接应用性质解决简单的实际问题;(2)会利用所给的方案构造示意图解决问题;(3)会初步设计解决实际问题的方案;(4)会实地测量和计算旗杆的高度、河的宽度。请大家自我反思一下,你是否掌握了本课时的阶段目标?再见下课了
这个问题的解决?教学目标1.本节课总目标是:会利用相似三角形的性质解决简单的实际问题。2.本课时阶段目标是:(1)会直接应用性质解决简单的实际问题;(2)会利用所给的方案构造示意图解决问题;(3)会初步设计解决实际问题的方案;(4)会实地测量和计算旗杆的高度、河的宽度。例题分析:测量金字塔的高度例:古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′ 与金字塔的影长AB,即可近似算出金字塔的高度OB。如果O′B′ =1米,A′B′=2米,AB=274米,求金字塔的高度OB。设置问题,引导研究问题一:预算与决策(应用相似性质解决问题) 某生活小区的居民筹集了1500元,计划在一块上、下底分别为10m、20m的梯形空地上的阴影部分处种植茉莉花,同时在茉莉花的周围小径上铺设健身鹅卵石(如图2)。他们发现:在ΔAMD地带上,种植茉莉花共花了160元,而铺设健身鹅卵石共花了200元,请你预算一下,他们所筹集的资金够用吗? 问题一:预算与决策问题二:测量大运河的宽度: 利用所给的方案构造示意图 大运河的两岸有一段是平行的,为了估算其运河的宽度,我们可以在对岸选定一个目标作为点A,再在运河的这一边选点B、C,使AB⊥BC,然后再选点E,使EC⊥BC,用视线确定BC和AE的交点为D。(1)想象一下,如何确定点的位置?如何画图?(2)要估算运河的宽度,你认为要测量哪些可以测量的线段?ABEDC图3(3)如果测得BD=120m,DC=60m,EC=50m,求出大运河的大致宽度AB。画出图形问题解决问题三:可以这样测量吗? 利用所给的方案构造示意图 河的两岸有一段是平行的,在河的这一岸每隔5m有一棵树,在那河的对岸每隔50m有一根电线杆,在离开岸25m处看对岸测得对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,你能根据以上信息画出示意图,并求出河宽吗? 50 m25 m20 mABCDE问题解决(2)根据题意可知:CD∥AB,AB=50m,CD=20m,DE=25m;设,河宽DE为x m.则EB = (x+25)m . ∵ CD∥AB,∴ΔECD∽ΔEAB. CD∶AB=ED∶EB,解得, x=37.5m.
答:这条河宽约为37.5m问题解决拓展延伸,促进发展问题:能通过这样的测量求出树高吗? 如图,教学楼旁边有一棵树,学习了相似三角形后,数学小组的同学们想利用树影测量树高。课外活动时在阳光下他们测得一根长为1米的竹杆的影长是0.9米,当他们马上测量树的影子长时,发现树的影子不全落在地面上,于是他们测得落在地面上的影子长2.7米,落在墙壁上的影长1.2米。1.2m2.7m拓展延伸,促进发展 如图,在某建筑物4m处有一棵树,在某时刻,1.2m长的竹竿竖直地面,影长为2m,此时,树的影子照射地面,还有一部分影子在建筑物的墙上,墙上的影长为2m,那么这棵树高约为多少m。A′ADCBB′C′课时目标,自我评价本课时的阶段目标是:(1)会直接应用性质解决简单的实际问题;(2)会利用所给的方案构造示意图解决问题;(3)会初步设计解决实际问题的方案;(4)会实地测量和计算旗杆的高度、河的宽度。请大家自我反思一下,你是否掌握了本课时的阶段目标?再见下课了
