18.1.1 平行四边形的性质学案
文档属性
| 名称 | 18.1.1 平行四边形的性质学案 |  | |
| 格式 | zip | ||
| 文件大小 | 629.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 23:34:15 | ||
图片预览

文档简介
18.1 平行四边形的性质1.
学习目标:
1. 了解平行四边形的定义
2. 能找出生活中的平行四边形并猜想平行四边形的对边、对角的数量关系
3. 任意画一个平行四边形并量一 量平行四边形的对边、对角的数量关系
4、根据猜想动手量会写出平行四边形的对边、对角的性质;
5、能根据平行四边形的性质进行简单的计算和证明;
学习重点:平行四边形的定义,平行四边形对角、对边相等的性质;
知识点回顾
定义:在平面内,由 条不在同一直线上的线段首尾顺次相接组成的图形叫做四边形.
四边形的内角和等于 度. 四边形的外角和等于 度.
课前自学:
在四边形中,最常见、价值最大的是平行四边形,如竹篱笆格子、推拉门、汽车防护链、书本等,都是平行四边形,平行四边形有哪些性质呢?
观察上图:两组对边分别 的四边形叫做平行四边形.
几何语言表述 ∵ AB∥CD AD∥BC ∴四边形ABCD是平行四边形
平行四边形的表示:用图形 “ ”表示, 如平行四边形ABCD记作; “ABCD ”
探索(B,C层次的学生完成1,2,4. A层次的学生完成1,2,3,4)
请你仔细观察身边有没有平行四边形图形:试猜想你看到的平行四边形的对边.对角有什么数量关系
请你动手画一个平行四边形图形:运用尺子,量角器量一量平行四边形的对边.对角有什么数量关系
( http: / / www.21cnjy.com )
A层次的同学你能运用以前所学的知识证明下题.试一试
如图,已知ABCD,求证:∠A=∠C, AB=DC (提示连接BD)
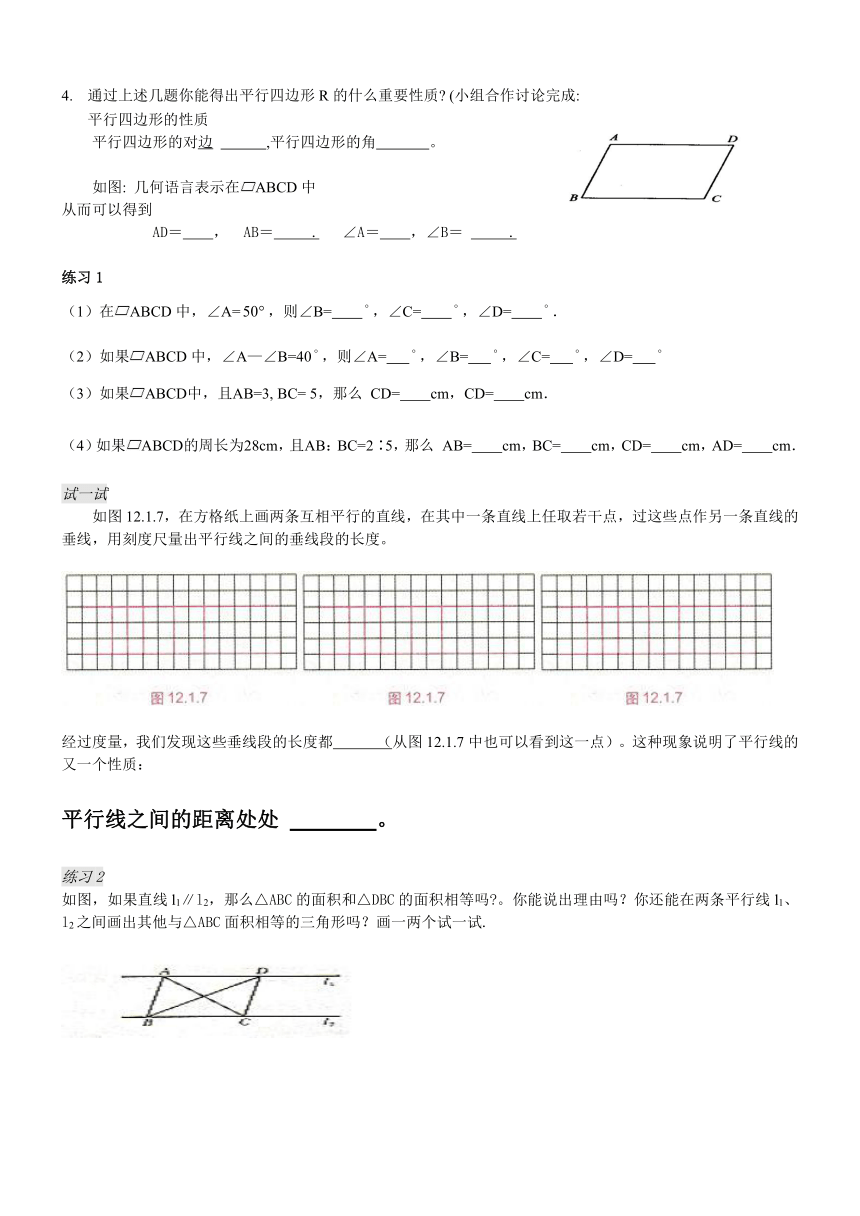
通过上述几题你能得出平行四边形R的什么重要性质 (小组合作讨论完成:
平行四边形的性质
平行四边形的对边 ,平行四边形的角 。
如图: 几何语言表示在ABCD中
从而可以得到
AD= , AB= . ∠A= ,∠B= .
练习1
(1)在ABCD中,∠A=,则∠B= ,∠C= ,∠D= .
(2)如果ABCD中,∠A—∠B=40,则∠A= ,∠B= ,∠C= ,∠D=
(3)如果ABCD中,且AB=3, BC= 5,那么 CD= cm,CD= cm.
(4)如果ABCD的周长为28cm,且AB:BC=2∶5,那么 AB= cm,BC= cm,CD= cm,AD= cm.
试一试
如图12.1.7,在方格纸上画两条互相 ( http: / / www.21cnjy.com )平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间的垂线段的长度。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
经过度量,我们发现这些垂线段的长度都 (从图12.1.7中也可以看到这一点)。这种现象说明了平行线的又一个性质:
平行线之间的距离处处 。
练习2
如图,如果直线l1∥l2,那么△ABC的面 ( http: / / www.21cnjy.com )积和△DBC的面积相等吗 。你能说出理由吗?你还能在两条平行线l1、l2之间画出其他与△ABC面积相等的三角形吗?画一两个试一试.
( http: / / www.21cnjy.com )
课堂小结(小组合作讨论共同完成):
1、平行四边形的定义:
(1)定义: 两组对边分别 的四边形叫做平行四边形。
(2)几何语言表述 ∵ AB∥CD AD∥BC ∴四边形ABCD是平行四边形
(3)平行四边形的表示:用图形 “ ”表示,如: “ ABCD” 读作平行四边形ABCD
2、平行四边形的性质
(1)共性:具有一般四边形的性质:四边形的内角和等于 度. 四边形的外角和等于 度.
(2)特性:
角 平行四边形的对边
边 平行四边形的对角
推论 夹在两条平行线间的平行线段 .
注意:平行四边形中对边是指无公共点的边,对 ( http: / / www.21cnjy.com )角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.
3、两条平行线的距离处处 。。
注意:(1)两相交直线无距离可言
(2)与两点的距离、点到直线的距离的区别与联系
应用练习 :(B.C)层次的学生完成
例1 如图在 ABCD中,已知∠B=40,求其余各个内角的度数。
解:由于平行四边形的对角相等,所以∠B=∠D=
因为 AD∥BC,
∠A=180-∠B = - =
所以 ∠C=∠A=
所以其余各个内角的度数分别为:
例2 如图,在 ABCD中,已知AB=5,周长等于24,求其余三条边的长。
解:由于平行四边形对边相等,所以
AB=DC= , AD=BC
所以AB+BC+CD+DA=24
解得 BC=
AD=BC=
所以其余三边的长分别为:
应用练习:B层次的学生完成
例3.在 ABCD中, AB=8, BC=10,求它的周长
应用练习:A层次的学生完成
例4 如图在 ABCD中,已知∠B=30,求其他各个内角的度数。
例5 如图, OABC的顶点O,A,C的坐标分别是(0,0),(a,0),(b,c), 则点B的坐标 。
( http: / / www.21cnjy.com )
课堂检测(B,C层次的学生完成1,2,,3,4题. A层次的学生完成第1,2,,3,4,5题)
1、在下列图形的性质中,平行四边形不一定具有的是( ).
(A)对角相等 (B)对角互补 (C)邻角互补 (D)内角和是
2、如图:在ABCD中,如果EF∥AD,GH∥CD,
EF与GH相交与点O,那么图中的平行四边形一共有( ).
(A)4个 (B)5个 (C)8个 (D)9个
3.在ABCD中,∠A=,则∠B= 度,∠C= 度,∠D= 度.
4.如果ABCD的周长为24cm,且AB =5,那么BC= cm,CD= cm,AD= cm.
5.已知.在ABCD中,BE平分∠ABC 交AD于E
.(1)若∠AEB=27,求∠C度数
(2)若AE=6cm,求CD长度
学习目标:
1. 了解平行四边形的定义
2. 能找出生活中的平行四边形并猜想平行四边形的对边、对角的数量关系
3. 任意画一个平行四边形并量一 量平行四边形的对边、对角的数量关系
4、根据猜想动手量会写出平行四边形的对边、对角的性质;
5、能根据平行四边形的性质进行简单的计算和证明;
学习重点:平行四边形的定义,平行四边形对角、对边相等的性质;
知识点回顾
定义:在平面内,由 条不在同一直线上的线段首尾顺次相接组成的图形叫做四边形.
四边形的内角和等于 度. 四边形的外角和等于 度.
课前自学:
在四边形中,最常见、价值最大的是平行四边形,如竹篱笆格子、推拉门、汽车防护链、书本等,都是平行四边形,平行四边形有哪些性质呢?
观察上图:两组对边分别 的四边形叫做平行四边形.
几何语言表述 ∵ AB∥CD AD∥BC ∴四边形ABCD是平行四边形
平行四边形的表示:用图形 “ ”表示, 如平行四边形ABCD记作; “ABCD ”
探索(B,C层次的学生完成1,2,4. A层次的学生完成1,2,3,4)
请你仔细观察身边有没有平行四边形图形:试猜想你看到的平行四边形的对边.对角有什么数量关系
请你动手画一个平行四边形图形:运用尺子,量角器量一量平行四边形的对边.对角有什么数量关系
( http: / / www.21cnjy.com )
A层次的同学你能运用以前所学的知识证明下题.试一试
如图,已知ABCD,求证:∠A=∠C, AB=DC (提示连接BD)
通过上述几题你能得出平行四边形R的什么重要性质 (小组合作讨论完成:
平行四边形的性质
平行四边形的对边 ,平行四边形的角 。
如图: 几何语言表示在ABCD中
从而可以得到
AD= , AB= . ∠A= ,∠B= .
练习1
(1)在ABCD中,∠A=,则∠B= ,∠C= ,∠D= .
(2)如果ABCD中,∠A—∠B=40,则∠A= ,∠B= ,∠C= ,∠D=
(3)如果ABCD中,且AB=3, BC= 5,那么 CD= cm,CD= cm.
(4)如果ABCD的周长为28cm,且AB:BC=2∶5,那么 AB= cm,BC= cm,CD= cm,AD= cm.
试一试
如图12.1.7,在方格纸上画两条互相 ( http: / / www.21cnjy.com )平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间的垂线段的长度。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
经过度量,我们发现这些垂线段的长度都 (从图12.1.7中也可以看到这一点)。这种现象说明了平行线的又一个性质:
平行线之间的距离处处 。
练习2
如图,如果直线l1∥l2,那么△ABC的面 ( http: / / www.21cnjy.com )积和△DBC的面积相等吗 。你能说出理由吗?你还能在两条平行线l1、l2之间画出其他与△ABC面积相等的三角形吗?画一两个试一试.
( http: / / www.21cnjy.com )
课堂小结(小组合作讨论共同完成):
1、平行四边形的定义:
(1)定义: 两组对边分别 的四边形叫做平行四边形。
(2)几何语言表述 ∵ AB∥CD AD∥BC ∴四边形ABCD是平行四边形
(3)平行四边形的表示:用图形 “ ”表示,如: “ ABCD” 读作平行四边形ABCD
2、平行四边形的性质
(1)共性:具有一般四边形的性质:四边形的内角和等于 度. 四边形的外角和等于 度.
(2)特性:
角 平行四边形的对边
边 平行四边形的对角
推论 夹在两条平行线间的平行线段 .
注意:平行四边形中对边是指无公共点的边,对 ( http: / / www.21cnjy.com )角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.
3、两条平行线的距离处处 。。
注意:(1)两相交直线无距离可言
(2)与两点的距离、点到直线的距离的区别与联系
应用练习 :(B.C)层次的学生完成
例1 如图在 ABCD中,已知∠B=40,求其余各个内角的度数。
解:由于平行四边形的对角相等,所以∠B=∠D=
因为 AD∥BC,
∠A=180-∠B = - =
所以 ∠C=∠A=
所以其余各个内角的度数分别为:
例2 如图,在 ABCD中,已知AB=5,周长等于24,求其余三条边的长。
解:由于平行四边形对边相等,所以
AB=DC= , AD=BC
所以AB+BC+CD+DA=24
解得 BC=
AD=BC=
所以其余三边的长分别为:
应用练习:B层次的学生完成
例3.在 ABCD中, AB=8, BC=10,求它的周长
应用练习:A层次的学生完成
例4 如图在 ABCD中,已知∠B=30,求其他各个内角的度数。
例5 如图, OABC的顶点O,A,C的坐标分别是(0,0),(a,0),(b,c), 则点B的坐标 。
( http: / / www.21cnjy.com )
课堂检测(B,C层次的学生完成1,2,,3,4题. A层次的学生完成第1,2,,3,4,5题)
1、在下列图形的性质中,平行四边形不一定具有的是( ).
(A)对角相等 (B)对角互补 (C)邻角互补 (D)内角和是
2、如图:在ABCD中,如果EF∥AD,GH∥CD,
EF与GH相交与点O,那么图中的平行四边形一共有( ).
(A)4个 (B)5个 (C)8个 (D)9个
3.在ABCD中,∠A=,则∠B= 度,∠C= 度,∠D= 度.
4.如果ABCD的周长为24cm,且AB =5,那么BC= cm,CD= cm,AD= cm.
5.已知.在ABCD中,BE平分∠ABC 交AD于E
.(1)若∠AEB=27,求∠C度数
(2)若AE=6cm,求CD长度
