22.1.1 二次函数 课件(共25张PPT)
文档属性
| 名称 | 22.1.1 二次函数 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
人教九上数学同步精品课件
人教版九年级上册
22.1.1 二次函数
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.了解二次函数的概念和一般形式.
2.会利用二次函数的概念解决问题
3.会列二次函数表达式解决实际问题.
学习目标
重点
难点
新课引入
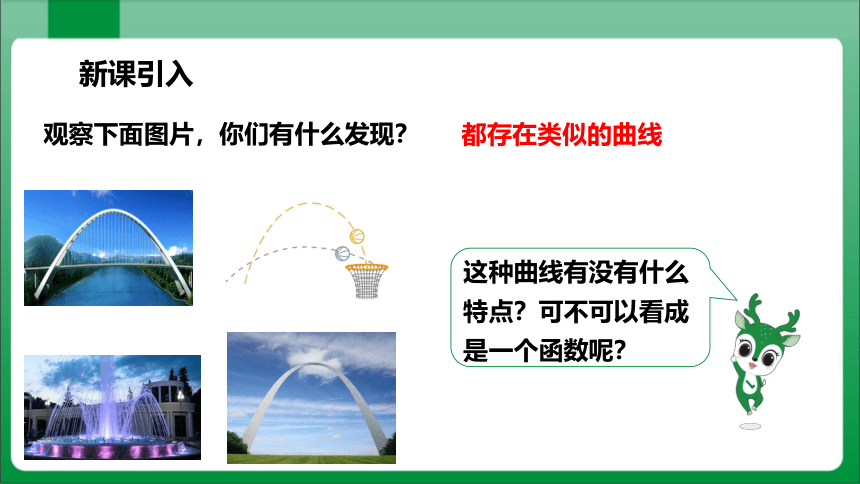
观察下面图片,你们有什么发现?
都存在类似的曲线
这种曲线有没有什么特点?可不可以看成是一个函数呢?
一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个_______的值,y 都有________确定的值与其对应,那么我们就说 x是________,y 是 x 的________.
确定
唯一
自变量
函数
1.什么是函数
回顾下列概念对比回答思考问题
2.一元二次方程的一般形式是什么?
ax2+bx+c=0 (a≠0).
新知学习
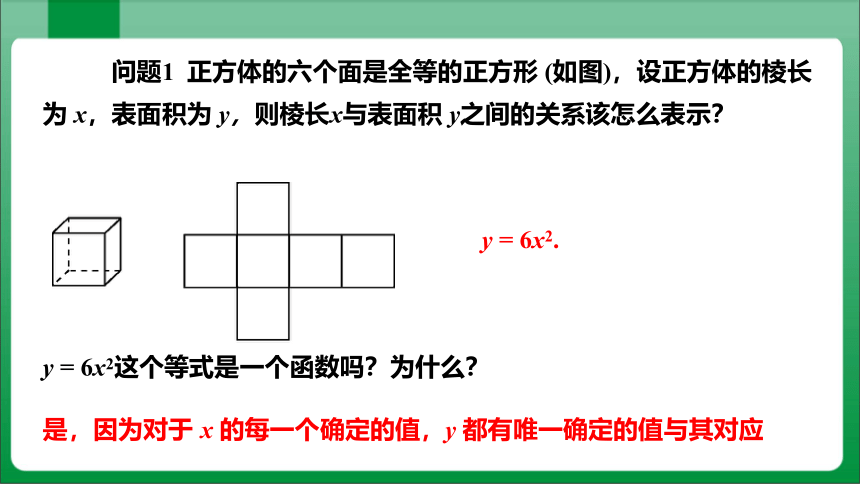
问题1 正方体的六个面是全等的正方形 (如图),设正方体的棱长为 x,表面积为 y,则棱长x与表面积 y之间的关系该怎么表示?
y = 6x2.
y = 6x2这个等式是一个函数吗?为什么?
是,因为对于 x 的每一个确定的值,y 都有唯一确定的值与其对应
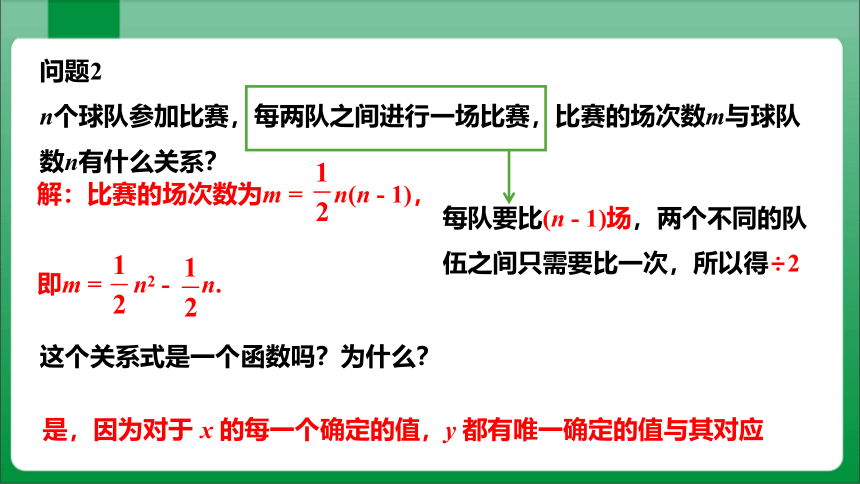
问题2
n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
解:比赛的场次数为m = n(n - 1),
即m = n2 - n.
这个关系式是一个函数吗?为什么?
是,因为对于 x 的每一个确定的值,y 都有唯一确定的值与其对应
每队要比(n - 1)场,两个不同的队伍之间只需要比一次,所以得÷2
问题3
某种产品现在的年产量是 20 t,计划今后两年增加产量. 如果每年都比上一年的产量增加 x 倍,那么两年后这种产品的产量 y 将随计划所定的 x 的值而确定,y 与 x 之间的关系应怎样表示?
解:两年后的产量 y = 20(1+x)2,
即 y = 20x2+40x+20.
这个关系式是一个函数吗?为什么?
是,因为对于 x 的每一个确定的值,y 都有唯一确定的值与其对应
比较
关系式 y=6x2 m= n2-n y=20x2+40x+20 相同点 注意事项
是不是函数
左
右
自变量取值范围(之前题目要求)
是
是
是
y
m
y
6x2
20x2+40x+20
n2-n
都是函数
因变量可以
是任何字母
只有一个字母
①自变量的最高次数是2
②都是整式
自变量可以有一次项也可以没有一次项
x>0
n≥2
x>0
自变量的取值范围由题目要求来决定
y=6x2,m= n2- n,y=20x2+40x+20 有什么共同点?
思考
1.都是函数;
2.函数解析式是整式;
3.自变量的最高次数是2;
一般地,形如 y=ax +bx+c ( a,b,c是常数,a≠ 0 ) 的函数叫做二次函数. 其中, x 是自变量,a,b,c 分别是函数解析式的二次项系数、一次项系数和常数项.
例1 下列函数中,哪些是二次函数?为什么?若是二次函数,请指出二次项系数,一次项系数和常数项.
① y=ax2+bx+c ② y=3-2x ③y=x2 ④
⑤ ⑥y=x +x +25 ⑦ y=(x+3) -x
不一定是,缺少a≠0的条件.
不是,x的最高次数是3.
不是、化简以后是一次函数
二次项系数:-2
一次项系数:0
常数项:3
二次项系数:1
一次项系数:0
常数项:0
二次项系数:-1
一次项系数:-2
常数项:0
不是,等式右边是分式.
二次函数关系式 二次项系数 一次项系数 常数项
y=3-2x -2 0 3
y=x2 1 0 0
y=-x -2x -1 -2 0
y=2x -x+8 2 -1 8
结论:
在判断二次函数时,必须满足:1.自变量的最高次数是2;
2.二次项系数a≠0;
b=0时,二次函数为y=ax +c (a≠ 0 )
b=0,c=0时,二次函数为y=ax (a≠ 0 )
c=0时,二次函数为y=ax +bx (a≠ 0 )
自变量系数和常数项都不为0时,二次函数为y=ax +bx +c(a≠ 0 )
例2 当m 取何值时,函数y=(m2+m)xm2-2m-1+(m-5)x+m2是关于x 的二次函数?并求出二次函数的解析式.
满足二次函数的条件是什么?
1.x的最高次数是2;
2.二次项系数不为0.
解:由题意,得
①m -2m-3=0 ,(m-3)(m+1)=0, m = 3或-1
②m(m+1) ≠ 0,m ≠ 0 或m ≠ -1
∴ m = 3.
∴当 m = 3 时,该函数是二次函数,
解析式为:y = (32+3)x32-2×3-1+(3-5)x+32, 即y = 12x2-2x+9.
例3 如图,用长为 45 m 的篱笆,一面利用墙 ( 墙的最大可用长度是 20 m ),围成中间有一道篱笆的矩形花圃,设花圃的一边长 AB 是 x ( 单位:m ),面积是 S ( 单位:m2 ).
(1) 求 S 与 x 的函数关系式及x的取值范围;
解:(1) S = x(45 - 3x) = -3x2 + 45x
( ≤ x < 15 ).
0<45 - 3x≤20
-45<- 3x ≤ -25
≤ x < 15
BC 是(45 - 3x)cm
S =AB · BC
解:(2) 当 AB= 5 时,
-3x2+45x
=-3×25+45×5
=150,
答:围成的面积是 150m .
(2) 当AB的长为5m时,围成的面积是多少?
(3) 当 S = 162 时,-3x2+45x = 162,
解得 x1 = 6,x2 = 9,
∵ ≤ x< 15,
∴ x = 9.
答:AB的长是 9m.
(3) 当AB 的长为多少米时,围成的面积为 162 m2?
随堂练习
1. 下列函数中,哪些是二次函数?
① y=ax2+bx+c ② y=4x +3 ③y=x2 +
④ ⑤ ⑥y=x +x +25
②③⑤
2.下列函数关系中,是二次函数的为( )
A.在弹性限度内,弹簧的长度y与所挂物体的质量x之间的关系.
B.距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆的面积S与半径之间的关系
D
3.己知函数y=(m2-2)x2+(m+ )x+8.
(1)若这个函数是一次函数,求出m的值;
(2)若这个函数是二次函数,求出m的取值范围.
解:(1)由题意得, ,解得
(2)由题意得, ,解得 且
4.如图,矩形绿地的长、宽各增加 x m,写出扩充后的绿地的面积 y
与 x 的关系式.
解:y=(30+x)(20+x)=x2+50x+600,
即 y=x2+50x+600.
x m
x m
30 m
20 m
长 为(20 + x)cm,宽为(30 + x)cm
5. 某网店销售某款童装,每件售价 60 元,每星期可卖 300 件. 为了促销,该网店决定降价销售. 市场调查反映,每降价 1 元,每星期可多卖 30 件. 已知该款童装每件的成本价为 40 元,设该款童装每件的售价为 x 元,每星期的销售量为 y 件.
(1) 求 y 与 x 之间的函数关系式,并写出自变量的取值范围;
(2) 设每星期的销售利润为 W 元,求 W 与 x 之间的函数关系式.
解:y=300+30 ( 60-x ) =-30x+2100 ( 40 ≤ x ≤ 60 ).
解:W= ( x-40 ) ( -30x+2 100 ) =-30x2+3300x-84000.
一般形式
特殊形式
定义
一般地,形如 y=ax +bx+c ( a,b,c是常数,a≠ 0 ) 的函数叫做二次函数. 其中, x 是自变量,a,b,c 分别是函数解析式的二次项系数、一次项系数和常数项.(自变量的最高次数是2;二次项系数a≠0)
y=ax2+bx+c(a,b,c是常数,a ≠0,)
y=ax2 (a ≠0);y=ax2+bx(a ≠0);
y=ax2+c(a ≠0,a,b,c是常数).
二次
函数
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
22.1.1 二次函数
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.了解二次函数的概念和一般形式.
2.会利用二次函数的概念解决问题
3.会列二次函数表达式解决实际问题.
学习目标
重点
难点
新课引入
观察下面图片,你们有什么发现?
都存在类似的曲线
这种曲线有没有什么特点?可不可以看成是一个函数呢?
一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个_______的值,y 都有________确定的值与其对应,那么我们就说 x是________,y 是 x 的________.
确定
唯一
自变量
函数
1.什么是函数
回顾下列概念对比回答思考问题
2.一元二次方程的一般形式是什么?
ax2+bx+c=0 (a≠0).
新知学习
问题1 正方体的六个面是全等的正方形 (如图),设正方体的棱长为 x,表面积为 y,则棱长x与表面积 y之间的关系该怎么表示?
y = 6x2.
y = 6x2这个等式是一个函数吗?为什么?
是,因为对于 x 的每一个确定的值,y 都有唯一确定的值与其对应
问题2
n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数m与球队数n有什么关系?
解:比赛的场次数为m = n(n - 1),
即m = n2 - n.
这个关系式是一个函数吗?为什么?
是,因为对于 x 的每一个确定的值,y 都有唯一确定的值与其对应
每队要比(n - 1)场,两个不同的队伍之间只需要比一次,所以得÷2
问题3
某种产品现在的年产量是 20 t,计划今后两年增加产量. 如果每年都比上一年的产量增加 x 倍,那么两年后这种产品的产量 y 将随计划所定的 x 的值而确定,y 与 x 之间的关系应怎样表示?
解:两年后的产量 y = 20(1+x)2,
即 y = 20x2+40x+20.
这个关系式是一个函数吗?为什么?
是,因为对于 x 的每一个确定的值,y 都有唯一确定的值与其对应
比较
关系式 y=6x2 m= n2-n y=20x2+40x+20 相同点 注意事项
是不是函数
左
右
自变量取值范围(之前题目要求)
是
是
是
y
m
y
6x2
20x2+40x+20
n2-n
都是函数
因变量可以
是任何字母
只有一个字母
①自变量的最高次数是2
②都是整式
自变量可以有一次项也可以没有一次项
x>0
n≥2
x>0
自变量的取值范围由题目要求来决定
y=6x2,m= n2- n,y=20x2+40x+20 有什么共同点?
思考
1.都是函数;
2.函数解析式是整式;
3.自变量的最高次数是2;
一般地,形如 y=ax +bx+c ( a,b,c是常数,a≠ 0 ) 的函数叫做二次函数. 其中, x 是自变量,a,b,c 分别是函数解析式的二次项系数、一次项系数和常数项.
例1 下列函数中,哪些是二次函数?为什么?若是二次函数,请指出二次项系数,一次项系数和常数项.
① y=ax2+bx+c ② y=3-2x ③y=x2 ④
⑤ ⑥y=x +x +25 ⑦ y=(x+3) -x
不一定是,缺少a≠0的条件.
不是,x的最高次数是3.
不是、化简以后是一次函数
二次项系数:-2
一次项系数:0
常数项:3
二次项系数:1
一次项系数:0
常数项:0
二次项系数:-1
一次项系数:-2
常数项:0
不是,等式右边是分式.
二次函数关系式 二次项系数 一次项系数 常数项
y=3-2x -2 0 3
y=x2 1 0 0
y=-x -2x -1 -2 0
y=2x -x+8 2 -1 8
结论:
在判断二次函数时,必须满足:1.自变量的最高次数是2;
2.二次项系数a≠0;
b=0时,二次函数为y=ax +c (a≠ 0 )
b=0,c=0时,二次函数为y=ax (a≠ 0 )
c=0时,二次函数为y=ax +bx (a≠ 0 )
自变量系数和常数项都不为0时,二次函数为y=ax +bx +c(a≠ 0 )
例2 当m 取何值时,函数y=(m2+m)xm2-2m-1+(m-5)x+m2是关于x 的二次函数?并求出二次函数的解析式.
满足二次函数的条件是什么?
1.x的最高次数是2;
2.二次项系数不为0.
解:由题意,得
①m -2m-3=0 ,(m-3)(m+1)=0, m = 3或-1
②m(m+1) ≠ 0,m ≠ 0 或m ≠ -1
∴ m = 3.
∴当 m = 3 时,该函数是二次函数,
解析式为:y = (32+3)x32-2×3-1+(3-5)x+32, 即y = 12x2-2x+9.
例3 如图,用长为 45 m 的篱笆,一面利用墙 ( 墙的最大可用长度是 20 m ),围成中间有一道篱笆的矩形花圃,设花圃的一边长 AB 是 x ( 单位:m ),面积是 S ( 单位:m2 ).
(1) 求 S 与 x 的函数关系式及x的取值范围;
解:(1) S = x(45 - 3x) = -3x2 + 45x
( ≤ x < 15 ).
0<45 - 3x≤20
-45<- 3x ≤ -25
≤ x < 15
BC 是(45 - 3x)cm
S =AB · BC
解:(2) 当 AB= 5 时,
-3x2+45x
=-3×25+45×5
=150,
答:围成的面积是 150m .
(2) 当AB的长为5m时,围成的面积是多少?
(3) 当 S = 162 时,-3x2+45x = 162,
解得 x1 = 6,x2 = 9,
∵ ≤ x< 15,
∴ x = 9.
答:AB的长是 9m.
(3) 当AB 的长为多少米时,围成的面积为 162 m2?
随堂练习
1. 下列函数中,哪些是二次函数?
① y=ax2+bx+c ② y=4x +3 ③y=x2 +
④ ⑤ ⑥y=x +x +25
②③⑤
2.下列函数关系中,是二次函数的为( )
A.在弹性限度内,弹簧的长度y与所挂物体的质量x之间的关系.
B.距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆的面积S与半径之间的关系
D
3.己知函数y=(m2-2)x2+(m+ )x+8.
(1)若这个函数是一次函数,求出m的值;
(2)若这个函数是二次函数,求出m的取值范围.
解:(1)由题意得, ,解得
(2)由题意得, ,解得 且
4.如图,矩形绿地的长、宽各增加 x m,写出扩充后的绿地的面积 y
与 x 的关系式.
解:y=(30+x)(20+x)=x2+50x+600,
即 y=x2+50x+600.
x m
x m
30 m
20 m
长 为(20 + x)cm,宽为(30 + x)cm
5. 某网店销售某款童装,每件售价 60 元,每星期可卖 300 件. 为了促销,该网店决定降价销售. 市场调查反映,每降价 1 元,每星期可多卖 30 件. 已知该款童装每件的成本价为 40 元,设该款童装每件的售价为 x 元,每星期的销售量为 y 件.
(1) 求 y 与 x 之间的函数关系式,并写出自变量的取值范围;
(2) 设每星期的销售利润为 W 元,求 W 与 x 之间的函数关系式.
解:y=300+30 ( 60-x ) =-30x+2100 ( 40 ≤ x ≤ 60 ).
解:W= ( x-40 ) ( -30x+2 100 ) =-30x2+3300x-84000.
一般形式
特殊形式
定义
一般地,形如 y=ax +bx+c ( a,b,c是常数,a≠ 0 ) 的函数叫做二次函数. 其中, x 是自变量,a,b,c 分别是函数解析式的二次项系数、一次项系数和常数项.(自变量的最高次数是2;二次项系数a≠0)
y=ax2+bx+c(a,b,c是常数,a ≠0,)
y=ax2 (a ≠0);y=ax2+bx(a ≠0);
y=ax2+c(a ≠0,a,b,c是常数).
二次
函数
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
