22.3.2 实际问题与二次函数-----利润问题 课件(共23张PPT)
文档属性
| 名称 | 22.3.2 实际问题与二次函数-----利润问题 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 08:13:22 | ||
图片预览







文档简介
(共23张PPT)
人教九上数学同步精品课件
人教版九年级上册
21.3.2 利润问题
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.能应用二次函数的性质解决商品销售过程中的最大利润问题.
2.明确商品销售问题中的数量关系及确定自变量的取值范围.
学习目标
重点
难点
我们去商场买衣服时,售货员一般都鼓励顾客多买,这样可以给顾客打折或降价,相应的每件的利润就少了,但是老板的收入会受到影响吗?怎样调整价格才能让利益最大化呢?
新课引入
二次函数与利润问题
例 某商品现在的售价为每件 60 元,每星期可卖出 300 件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
新知学习
你知道这些数量关系吗?
(1)销售额= 售价×销售量;
(2)利润= 销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
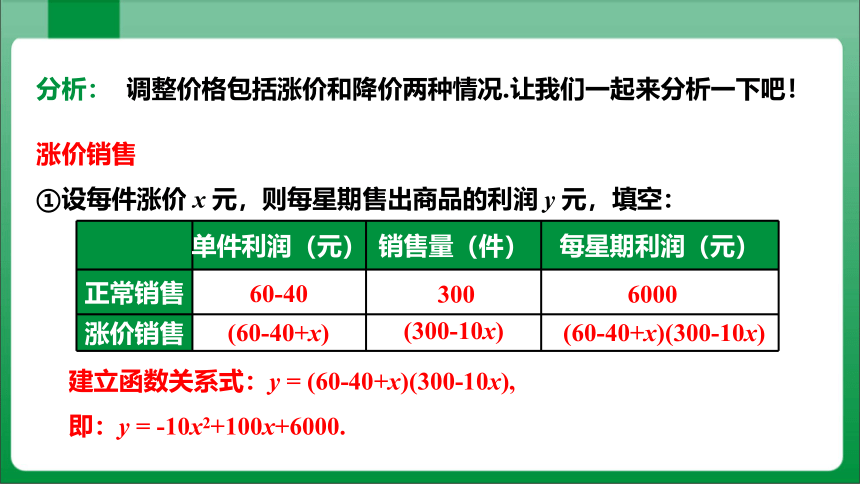
分析: 调整价格包括涨价和降价两种情况.让我们一起来分析一下吧!
涨价销售
①设每件涨价 x 元,则每星期售出商品的利润 y 元,填空:
建立函数关系式:y = (60-40+x)(300-10x),
即:y = -10x2+100x+6000.
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
60-40
300
(60-40+x)
(300-10x)
(60-40+x)(300-10x)
6000
②自变量 x 的取值范围如何确定?
营销规律是价格上涨,销量下降,因此需要考虑销售量不为负,故300-10x ≥0,且 x ≥ 0,因此自变量的取值范围是 0 ≤ x ≤ 30.
③涨价多少元时,利润最大,最大利润是多少?
y = -10x2+100x+6000,
所以当 时,y = -10×52+100×5+6000 = 6250.
即涨价 5 元时,最大利润是 6250 元.
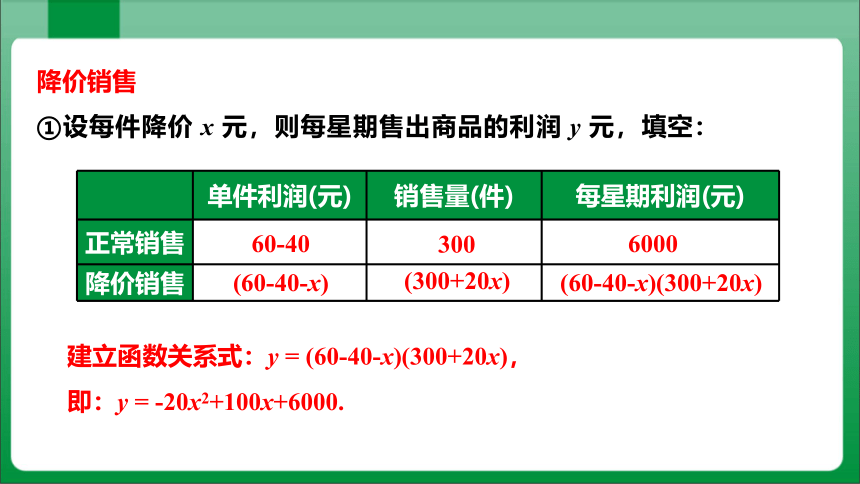
建立函数关系式:y = (60-40-x)(300+20x),
即:y = -20x2+100x+6000.
降价销售
①设每件降价 x 元,则每星期售出商品的利润 y 元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
降价销售
60-40
300
(60-40-x)
(300+20x)
(60-40-x)(300+20x)
6000
营销规律是价格下降,销量上升,因此需要考虑单件利润不为负,故 20-x ≥ 0,且x ≥ 0,因此自变量的取值范围是0 ≤ x ≤20.
③降价多少元时,利润最大,最大利润是多少?
即降价 2.5 元时,最大利润是 6125 元.
∵6125<6250
∴综上可知,定价 57.5 元时,最大利润是 6125 元.
y = -20x2 + 100x + 6000,
②自变量x的取值范围如何确定?
当 时,
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
归纳
求解最大利润问题的一般步骤
1. 建立利润与价格之间的函数关系式:运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”;
2. 结合实际意义,确定自变量的取值范围;
3. 在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
随堂练习
1.某种商品每天的销售利润y (元)与销售单价x (元)之间满足关系:y=ax2+bx-75.其图象如图.
(1) 销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由图可以看出:二次函数y=ax+bx-75过点(5,0)、(7,16),
将两点坐标代入解析式即可求得:
y=-x2+20x-75,即y=-(x-10)2+25.
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最大,为25元.
(2) 销售单价在什么范围时,该种商品每天的销售利润不低于16元?
(2)显然,当y=16时,x1=7、x2=13.
∵y=-x+20x-75图象的对称轴为x=10,
∴点(7,16)关于对称轴的对称点为(13,16),
结合图象分析得,
销售单价在7 ≤x ≤13时,利润不低于16元.
13
2.一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元/件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x/(元/件) 4 5 6
y/件 10 000 9 500 9 000
(1)求y与x的函数关系式(不求自变量的取值范围);
解:(1)设y与x的函数关系式为y=kx+b(k≠0),代入
,解得 .
∴y=-500x+12 000;
(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6 000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(2)由题意得 ,解得3≤x≤12.
设利润为w元,根据题意得,
w=(x-3)y=(x-3)(-500x+12 000)=-500x2+13 500x-36 000
=-500(x-13.5)2+55 125,
∵﹣500<0,∴当x<13.5时,w随x的增大而增大.
∵3≤x≤12,
∴当x=12时,w取最大值-500×(12-13.5)2+55 125=54 000. 答:这一周该商场销售这种商品获得的最大利润为54 000元,售价为12元.
(3)抗疫期间,该商场这种商品售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠m元(1≤m≤6),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
思路点拨:每件捐赠m元,也就是每件的利润少m元
∵﹣500<0,∴当x≤13.5+0.5m时,w随x的增大而增大.
∵捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.
∴15≤13.5+0.5m,解得,m≥3.
∵1≤m≤6,∴3≤m≤6.
(3)根据题意得,w=(x-3-m)(-500x+12 000)
=-500x2+(13 500+500m)x-36 000-12 000m,
所以对称轴为 .
利
润
问
题
建立函数关系式
确定最大利润
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取
值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
利用配方法或公式求最大值或利用函数简图和性质求出.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
21.3.2 利润问题
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.能应用二次函数的性质解决商品销售过程中的最大利润问题.
2.明确商品销售问题中的数量关系及确定自变量的取值范围.
学习目标
重点
难点
我们去商场买衣服时,售货员一般都鼓励顾客多买,这样可以给顾客打折或降价,相应的每件的利润就少了,但是老板的收入会受到影响吗?怎样调整价格才能让利益最大化呢?
新课引入
二次函数与利润问题
例 某商品现在的售价为每件 60 元,每星期可卖出 300 件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
新知学习
你知道这些数量关系吗?
(1)销售额= 售价×销售量;
(2)利润= 销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
分析: 调整价格包括涨价和降价两种情况.让我们一起来分析一下吧!
涨价销售
①设每件涨价 x 元,则每星期售出商品的利润 y 元,填空:
建立函数关系式:y = (60-40+x)(300-10x),
即:y = -10x2+100x+6000.
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
60-40
300
(60-40+x)
(300-10x)
(60-40+x)(300-10x)
6000
②自变量 x 的取值范围如何确定?
营销规律是价格上涨,销量下降,因此需要考虑销售量不为负,故300-10x ≥0,且 x ≥ 0,因此自变量的取值范围是 0 ≤ x ≤ 30.
③涨价多少元时,利润最大,最大利润是多少?
y = -10x2+100x+6000,
所以当 时,y = -10×52+100×5+6000 = 6250.
即涨价 5 元时,最大利润是 6250 元.
建立函数关系式:y = (60-40-x)(300+20x),
即:y = -20x2+100x+6000.
降价销售
①设每件降价 x 元,则每星期售出商品的利润 y 元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
降价销售
60-40
300
(60-40-x)
(300+20x)
(60-40-x)(300+20x)
6000
营销规律是价格下降,销量上升,因此需要考虑单件利润不为负,故 20-x ≥ 0,且x ≥ 0,因此自变量的取值范围是0 ≤ x ≤20.
③降价多少元时,利润最大,最大利润是多少?
即降价 2.5 元时,最大利润是 6125 元.
∵6125<6250
∴综上可知,定价 57.5 元时,最大利润是 6125 元.
y = -20x2 + 100x + 6000,
②自变量x的取值范围如何确定?
当 时,
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
归纳
求解最大利润问题的一般步骤
1. 建立利润与价格之间的函数关系式:运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”;
2. 结合实际意义,确定自变量的取值范围;
3. 在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
随堂练习
1.某种商品每天的销售利润y (元)与销售单价x (元)之间满足关系:y=ax2+bx-75.其图象如图.
(1) 销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由图可以看出:二次函数y=ax+bx-75过点(5,0)、(7,16),
将两点坐标代入解析式即可求得:
y=-x2+20x-75,即y=-(x-10)2+25.
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最大,为25元.
(2) 销售单价在什么范围时,该种商品每天的销售利润不低于16元?
(2)显然,当y=16时,x1=7、x2=13.
∵y=-x+20x-75图象的对称轴为x=10,
∴点(7,16)关于对称轴的对称点为(13,16),
结合图象分析得,
销售单价在7 ≤x ≤13时,利润不低于16元.
13
2.一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元/件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x/(元/件) 4 5 6
y/件 10 000 9 500 9 000
(1)求y与x的函数关系式(不求自变量的取值范围);
解:(1)设y与x的函数关系式为y=kx+b(k≠0),代入
,解得 .
∴y=-500x+12 000;
(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6 000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(2)由题意得 ,解得3≤x≤12.
设利润为w元,根据题意得,
w=(x-3)y=(x-3)(-500x+12 000)=-500x2+13 500x-36 000
=-500(x-13.5)2+55 125,
∵﹣500<0,∴当x<13.5时,w随x的增大而增大.
∵3≤x≤12,
∴当x=12时,w取最大值-500×(12-13.5)2+55 125=54 000. 答:这一周该商场销售这种商品获得的最大利润为54 000元,售价为12元.
(3)抗疫期间,该商场这种商品售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠m元(1≤m≤6),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
思路点拨:每件捐赠m元,也就是每件的利润少m元
∵﹣500<0,∴当x≤13.5+0.5m时,w随x的增大而增大.
∵捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.
∴15≤13.5+0.5m,解得,m≥3.
∵1≤m≤6,∴3≤m≤6.
(3)根据题意得,w=(x-3-m)(-500x+12 000)
=-500x2+(13 500+500m)x-36 000-12 000m,
所以对称轴为 .
利
润
问
题
建立函数关系式
确定最大利润
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取
值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
利用配方法或公式求最大值或利用函数简图和性质求出.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
