数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系 课件(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系 课件(共30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 11:43:16 | ||
图片预览







文档简介
(共30张PPT)
2.5.2圆与圆的位置关系
学习目标
素 养 目 标 学 科 素 养
1.理解圆与圆的位置关系的种类;(重点) 2.会用代数法和几何法来判断圆与圆的位置关系;(难点) 3.体会根据圆的对称性灵活处理问题的方法和它的优越性.(重点、难点) 1、直观想象
2、数学运算
3、逻辑推理
引言
3圆与圆位置关系的应用
平面几何中的圆与圆位置关系的定义及判断方法
1回顾圆与圆的位置关系
2用代数法判断位置关系
类比直线与圆位置关系的判定方法归纳提炼
求动点轨迹问题
问题1 圆与圆有哪些位置关系?
A .相离、相切、相交
B.外离、外切、相交、内切、内含
探究新知
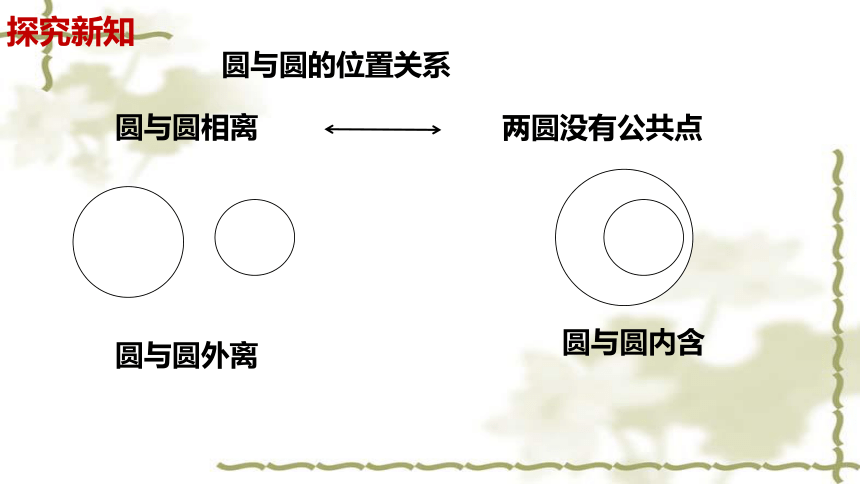
圆与圆的位置关系
圆与圆相离
两圆没有公共点
圆与圆外离
圆与圆内含
探究新知
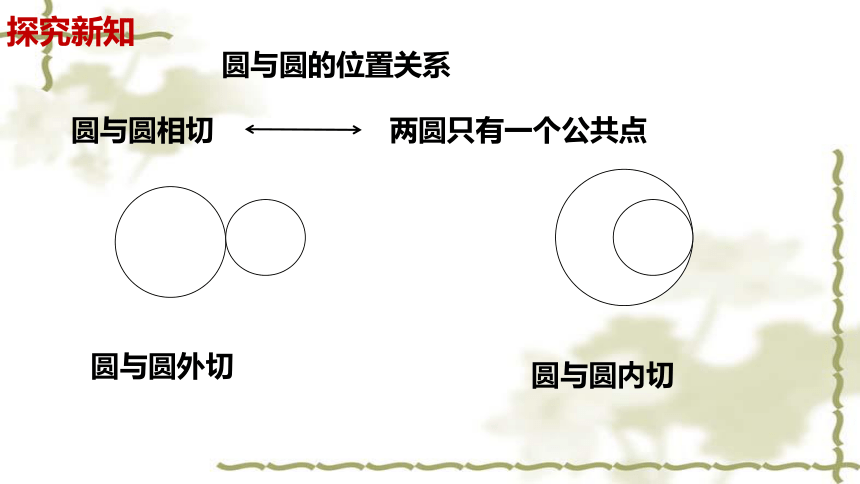
圆与圆的位置关系
圆与圆相切
两圆只有一个公共点
圆与圆外切
圆与圆内切
探究新知
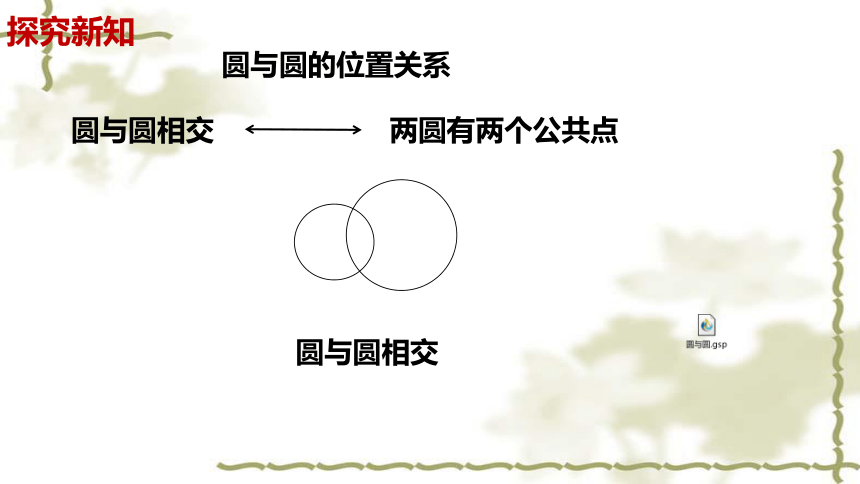
圆与圆的位置关系
圆与圆相交
两圆有两个公共点
圆与圆相交
探究新知
探究一:根据圆的方程,用几何法探索圆与圆的位置位置
探究新知
探究新知
外离
内含
外切
内切
圆与圆的位置关系
相交
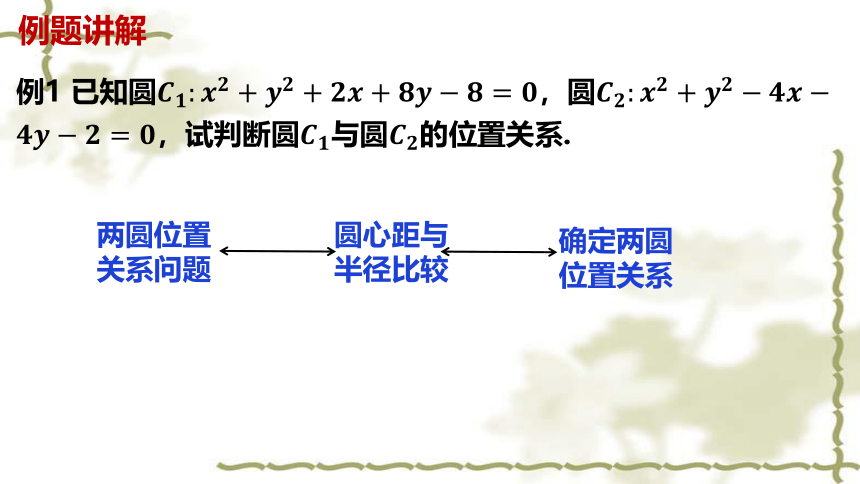
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
两圆位置
关系问题
圆心距与
半径比较
确定两圆
位置关系
例1 已知圆,圆,试判断圆与圆的位置关系.
解法1:
y
x
A
B
C2
C1
例题讲解
把圆的方程化成标准方程得
,
圆的圆心是(1,4),半径=5.
把圆的方程化成标准方程,得
,
圆的圆心是(2,2),半径=.
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
解法1:
y
x
A
B
C2
C1
圆与圆的连心线的长为.
圆与圆的两半径之和=5+,
两半径之差=5.
因为,
即<|| <,
所以圆与圆相交,它们有两个公共点A,B.
探究新知
探究二:用代数法探索圆与圆的位置关系
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
两圆位置
关系问题
公共点
的个数
确定两圆
位置关系
联立方程组解的情况
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
解法2:
将圆与圆的方程联立,得到方程组
① ②,得 ③
由③,得.把上式代入①。
并整理,得 ④
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
解法2:
y
x
A
B
C2
C1
方程④的根的判别式
,
所以,方程④有两个不相等的实数根
, .
把, 分别代入方程③,得到
y1,y2.
因此圆与圆有两个公共点A(),B(
追问1:你能求出公共弦所在直线方程吗?
解法2:
① ②,得 ③
④
.
y1, y2.
例题讲解
圆与圆有两个公共点A(),B(
追问1:你能求出公共弦所在直线方程吗?
解法2:
① ②,得 ③
两圆相交时,公共弦所在直线方程
例题讲解
探究新知
追问3:如果所求=0或0,说明 什么呢?
外离
内含
=0
外切
内切
0
两圆位置
关系问题
判断两圆位置关系
解法1
解法2
探究新知
判断圆和圆位置关系问题的方法
联立方程组解的情况
圆心距与
半径比较
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
求轨迹
求轨迹方程
得到轨迹
轨迹与圆的位置关系
轨迹方程与圆的方程联立方程组的解的情况
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
A
B
y
x
O
解:如图,以线段AB的中点O为原点,AB所在直线为轴,线段AB的垂直平分线为y轴,建立平面直角坐标系. 由AB=4,得A(2,0),B (2,0).
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
A
B
y
x
O
M
P
轨迹方程
轨迹
设点M的坐标为,
由 ,
得,
化简得,
即.
所以点M轨迹是以P(6,0)为圆心,半径为的一个圆.
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
A
B
y
x
O
M
P
因为两圆的圆心距为|PO|=6,
两圆的半径分别为=2,
,
又<|PO|<
,
所以点M的轨迹与圆O相交.
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
A
B
y
x
O
M
P
所以点M的轨迹与圆O相交.
y1, y2.
例题讲解
追问:如果把本例中的“倍”改为“>0)倍”你能分析并解决这个问题吗?
设点M的坐标为(x,y),由|MA|=k|MB|,
得,
化简,得
.
当k=1时,方程为=0,可知点M的轨迹是线段AB的垂直平分线;
当k>0,且k ≠1时,方程可化为,
点M的轨迹是以(,0)为圆心,半径为的圆.
随堂检测
1.已知圆:,圆:,判断圆与圆的位置关系.
2.已知圆:,圆:,证明圆与圆相交,并求圆与圆:的公共弦所在直线的方程.
随堂检测
坐标法求动点轨迹问题得基本步骤
第一步
第二步
第三步
建立适当的平面直角坐标系.
寻找动点满足的几何关系.
将几何问题用方程表示.
代数化简、变形,得到轨迹方程.
把轨迹方程“翻译”成轨迹.
探究新知
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
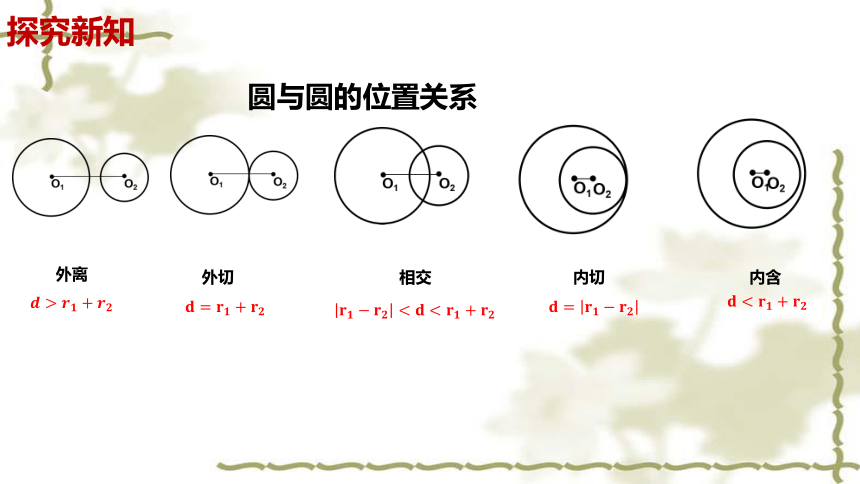
外离:
内含:
外切:
内切:
相交:
小结
d为圆心距
为两圆半径
2.5.2圆与圆的位置关系
学习目标
素 养 目 标 学 科 素 养
1.理解圆与圆的位置关系的种类;(重点) 2.会用代数法和几何法来判断圆与圆的位置关系;(难点) 3.体会根据圆的对称性灵活处理问题的方法和它的优越性.(重点、难点) 1、直观想象
2、数学运算
3、逻辑推理
引言
3圆与圆位置关系的应用
平面几何中的圆与圆位置关系的定义及判断方法
1回顾圆与圆的位置关系
2用代数法判断位置关系
类比直线与圆位置关系的判定方法归纳提炼
求动点轨迹问题
问题1 圆与圆有哪些位置关系?
A .相离、相切、相交
B.外离、外切、相交、内切、内含
探究新知
圆与圆的位置关系
圆与圆相离
两圆没有公共点
圆与圆外离
圆与圆内含
探究新知
圆与圆的位置关系
圆与圆相切
两圆只有一个公共点
圆与圆外切
圆与圆内切
探究新知
圆与圆的位置关系
圆与圆相交
两圆有两个公共点
圆与圆相交
探究新知
探究一:根据圆的方程,用几何法探索圆与圆的位置位置
探究新知
探究新知
外离
内含
外切
内切
圆与圆的位置关系
相交
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
两圆位置
关系问题
圆心距与
半径比较
确定两圆
位置关系
例1 已知圆,圆,试判断圆与圆的位置关系.
解法1:
y
x
A
B
C2
C1
例题讲解
把圆的方程化成标准方程得
,
圆的圆心是(1,4),半径=5.
把圆的方程化成标准方程,得
,
圆的圆心是(2,2),半径=.
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
解法1:
y
x
A
B
C2
C1
圆与圆的连心线的长为.
圆与圆的两半径之和=5+,
两半径之差=5.
因为,
即<|| <,
所以圆与圆相交,它们有两个公共点A,B.
探究新知
探究二:用代数法探索圆与圆的位置关系
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
两圆位置
关系问题
公共点
的个数
确定两圆
位置关系
联立方程组解的情况
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
解法2:
将圆与圆的方程联立,得到方程组
① ②,得 ③
由③,得.把上式代入①。
并整理,得 ④
例题讲解
例1 已知圆,圆,试判断圆与圆的位置关系.
解法2:
y
x
A
B
C2
C1
方程④的根的判别式
,
所以,方程④有两个不相等的实数根
, .
把, 分别代入方程③,得到
y1,y2.
因此圆与圆有两个公共点A(),B(
追问1:你能求出公共弦所在直线方程吗?
解法2:
① ②,得 ③
④
.
y1, y2.
例题讲解
圆与圆有两个公共点A(),B(
追问1:你能求出公共弦所在直线方程吗?
解法2:
① ②,得 ③
两圆相交时,公共弦所在直线方程
例题讲解
探究新知
追问3:如果所求=0或0,说明 什么呢?
外离
内含
=0
外切
内切
0
两圆位置
关系问题
判断两圆位置关系
解法1
解法2
探究新知
判断圆和圆位置关系问题的方法
联立方程组解的情况
圆心距与
半径比较
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
求轨迹
求轨迹方程
得到轨迹
轨迹与圆的位置关系
轨迹方程与圆的方程联立方程组的解的情况
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
A
B
y
x
O
解:如图,以线段AB的中点O为原点,AB所在直线为轴,线段AB的垂直平分线为y轴,建立平面直角坐标系. 由AB=4,得A(2,0),B (2,0).
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
A
B
y
x
O
M
P
轨迹方程
轨迹
设点M的坐标为,
由 ,
得,
化简得,
即.
所以点M轨迹是以P(6,0)为圆心,半径为的一个圆.
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
A
B
y
x
O
M
P
因为两圆的圆心距为|PO|=6,
两圆的半径分别为=2,
,
又<|PO|<
,
所以点M的轨迹与圆O相交.
例题讲解
例2 已知圆的直径,动点M与点A的距离是它与点B的距离的倍. 试探究点M的轨迹,并判断该轨迹与圆的位置关系.
A
B
y
x
O
M
P
所以点M的轨迹与圆O相交.
y1, y2.
例题讲解
追问:如果把本例中的“倍”改为“>0)倍”你能分析并解决这个问题吗?
设点M的坐标为(x,y),由|MA|=k|MB|,
得,
化简,得
.
当k=1时,方程为=0,可知点M的轨迹是线段AB的垂直平分线;
当k>0,且k ≠1时,方程可化为,
点M的轨迹是以(,0)为圆心,半径为的圆.
随堂检测
1.已知圆:,圆:,判断圆与圆的位置关系.
2.已知圆:,圆:,证明圆与圆相交,并求圆与圆:的公共弦所在直线的方程.
随堂检测
坐标法求动点轨迹问题得基本步骤
第一步
第二步
第三步
建立适当的平面直角坐标系.
寻找动点满足的几何关系.
将几何问题用方程表示.
代数化简、变形,得到轨迹方程.
把轨迹方程“翻译”成轨迹.
探究新知
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
外离:
内含:
外切:
内切:
相交:
小结
d为圆心距
为两圆半径
