数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系(共38张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系(共38张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 11:43:39 | ||
图片预览





文档简介
(共38张PPT)
2.5.1直线与圆的位置关系
第一课时
学习目标
素 养 目 标 学 科 素 养
1.掌握直线与圆的三种位置关系:相交,相切,相离;(重点) 2.会用代数法和几何法来判断直线与圆的三种位置关系;(难点) 3.会用直线与圆的位置关系解决一些实际问题.(重点、难点) 1、直观想象
2、数学运算
3、数形结合
前面我们学习了直线的方程、圆的方程,用直线的方程研究了两条直线的位置关系,本节课我们类比用直线的方程研究两直线位置关系的方法,运用直线与圆的方程,研究直线与圆的的位置关系.
引言
探究新知
探究新知
探究一:用代数方式判断直线与圆的位置关系
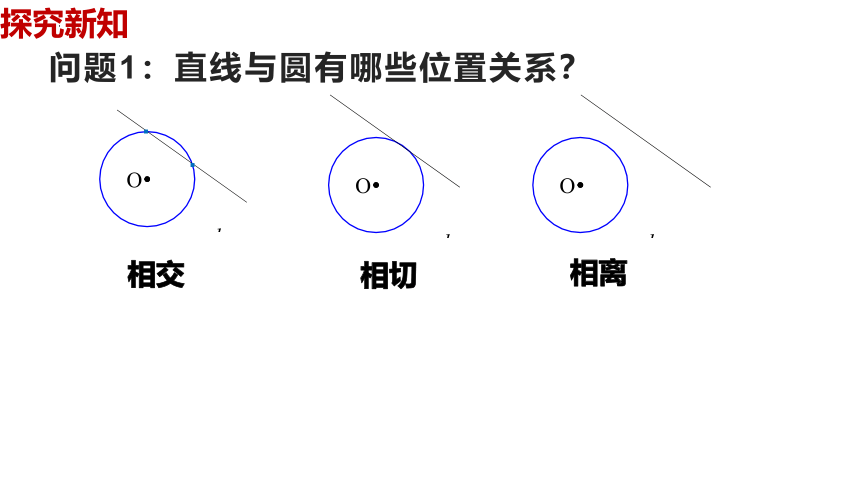
相交
相切
相离
.
.
问题1:直线与圆有哪些位置关系?
探究新知
相交
相切
相离
.
.
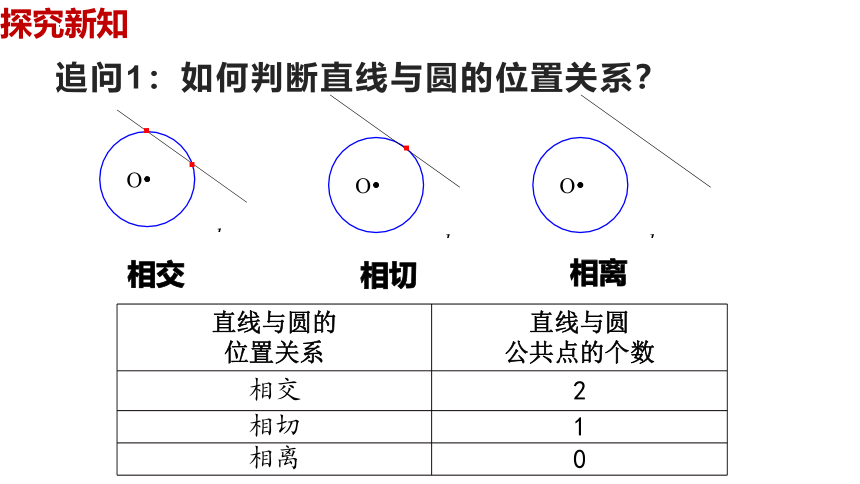
直线与圆的 位置关系 直线与圆
公共点的个数
相交 2
相切 1
相离 0
.
探究新知
追问1:如何判断直线与圆的位置关系?
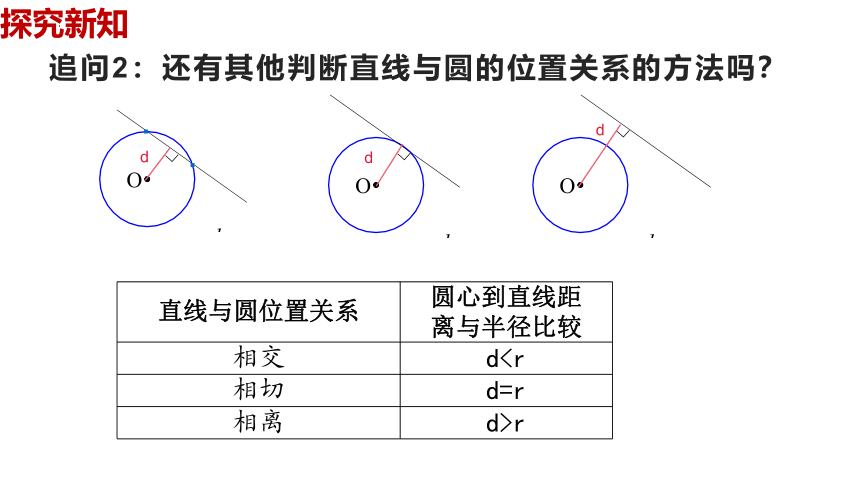
追问2:还有其他判断直线与圆的位置关系的方法吗?
.
.
d
∟
d
∟
d
∟
直线与圆位置关系 圆心到直线距
离与半径比较
相交 d相切 d=r
相离 d>r
探究新知
.
.
d
∟
d
∟
d
∟
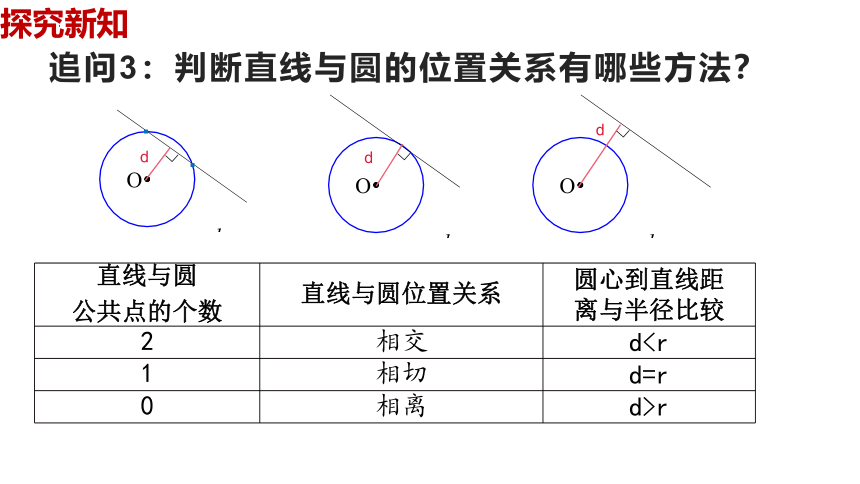
追问3:判断直线与圆的位置关系有哪些方法?
直线与圆 公共点的个数 直线与圆位置关系 圆心到直线距
离与半径比较
2 相交 d1 相切 d=r
0 相离 d>r
探究新知
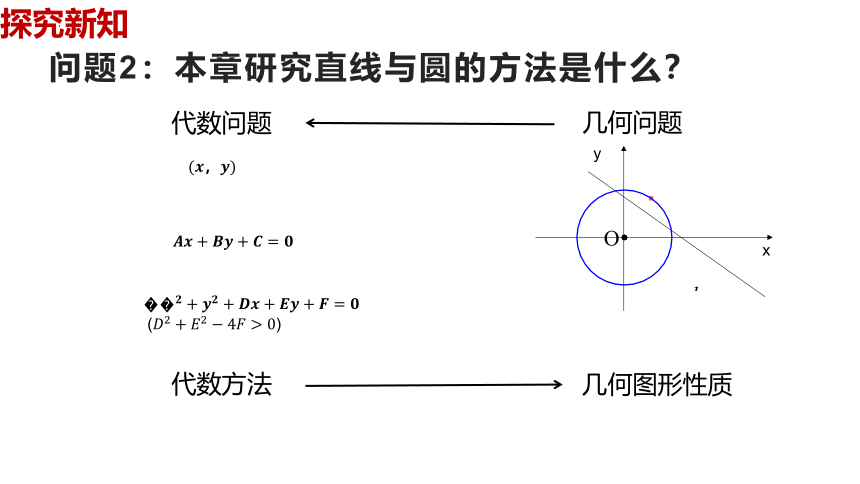
问题2:本章研究直线与圆的方法是什么?
x
y
.
,
()
几何问题
代数问题
几何图形性质
代数方法
探究新知
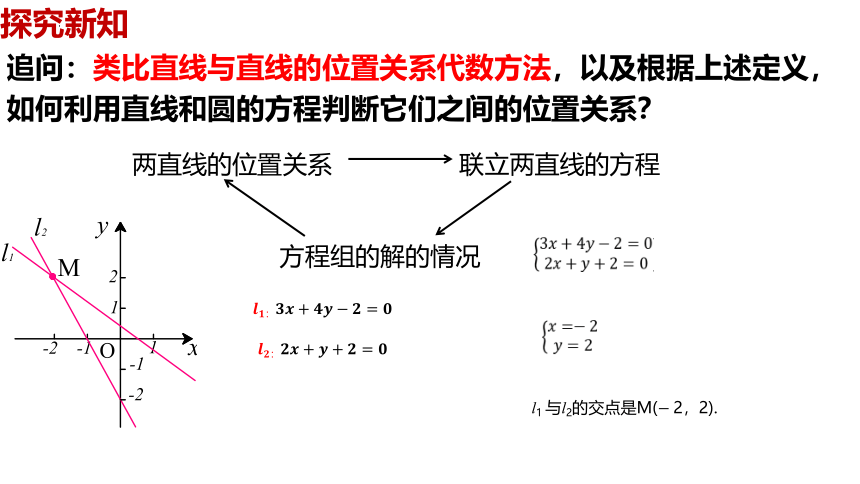
追问:类比直线与直线的位置关系代数方法,以及根据上述定义,如何利用直线和圆的方程判断它们之间的位置关系?
两直线的位置关系
联立两直线的方程
方程组的解的情况
探究新知
l1 与l2的交点是M(2,2).
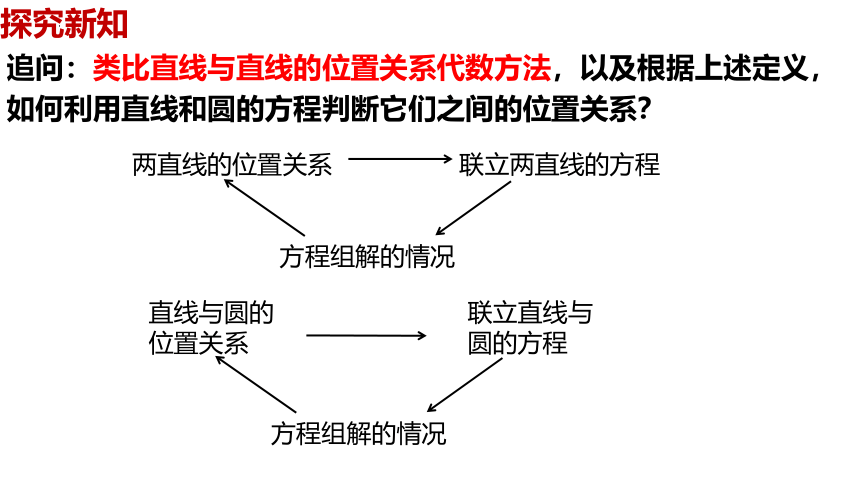
追问:类比直线与直线的位置关系代数方法,以及根据上述定义,如何利用直线和圆的方程判断它们之间的位置关系?
两直线的位置关系
联立两直线的方程
方程组解的情况
直线与圆的位置关系
联立直线与
圆的方程
方程组解的情况
探究新知
例题讲解
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
追问1:直线与圆的方程联立组成的方程组,如何判断解的个数?
消去,得,
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
方程有两组实数解
直线与圆相交
例题讲解
方程有一组实数解
直线与圆相切
方程没有实数解
直线与圆相离
代数法:联立方程
例题讲解
解法1:联立直线与圆C的方程,得
消去,得,
解得,.
所以,直线与圆相交,有两个公共点.
把,分别代入方程①,得.
所以,直线与圆C的两个交点是
因此|AB| =.
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
追问2:研究直线与圆的位置关系问题的基本思路是什么?
几何———代数
联立,解方程组
思路1
代数———几何
位置关系
公共点的个数
探究新知
追问3:还有其他方法判断直线与圆的位置关系吗?
几何———代数
求d与r
思路2
代数———几何
位置关系
d
∟
探究新知
d与r的比较
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
例题讲解
解法2:圆C的方程可化为
,
因此圆心C的坐标为(0,1),半径为,
圆心C(0,1)到直线的距离
追问4:如何求圆心到直线的距离?
.
(其中A,B不同时为0)
点P到直线的距离
探究新知
几何法:数形结合
解法2:圆C的方程可化为
,
因此圆心C的坐标为(0,1),半径为,
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
圆心C(0,1)到直线l的距离
.
所以,直线与圆C相交,有两个公共点.
如图,由垂径定理,得.
例题讲解
判断直线与圆的位置关系的方法
直线与圆相交
直线与圆相切
直线与圆相离
小结:
法1:联立方程
法2:比较d与r
两组解
一组解
无解
dd=r
d>r
探究新知
代数法是直接运用直线和圆的方程组成的方程组有无实数解的情况判断直线与圆的位置关系,是完全代数的方法;具有程序性、普适性.
几何法是利用图形中的相关几何量(圆心到直线的距离、圆的半径)的大小判断直线与圆的位置关系,涉及圆心到直线距离的计算。利用图形的几何性质,有助于简化计算.(数形结合)
代数法与几何法的比较:
探究新知
探究新知
探究二:圆的切线方程
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
P(2,1)
例题讲解
追问1:过圆外一点作圆的切线,能作出几条?
例2 过点作圆的切线,求切线的方程.
追问1:过圆外一点作圆的切线,能作出几条?
x
y
O
P(2,1)
追问2:如何刻画直线与圆相切?
公共点的个数;
圆心到直线的距离
追问3:直线的方程选择什么形式?
点斜式;两点式
例题讲解
过圆外一点可以作圆的两条切线
例题讲解
例2 过点作圆的切线,求切线的方程.
几何法
x
y
O
P(2,1)
点斜式
解法1:
d=r
代数法
解法2:
,
.
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
x=2
解法1:
设切线的斜率为,则切线的方程为
,
因为直线l与圆相切,所以方程组
只有一组解.
例题讲解
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
解法1:
x=2
例题讲解
消元,得.
因为方程①只有一个解,所以
,
解得=0或.
所以,所求切线的方程为=1,或.
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
x=2
解法2:
设切线的斜率为,则切线的方程为
,即.
由圆心(0,0)到切线的距离等于圆的半径1,
得
,解得=0或.
或.
因此,所求切线的方程为y=1
例题讲解
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
两点式
例题讲解
∟
追问4:你能比较这两种方法的差异吗?
直线与圆相切
直线方程
思路1
直线的方程
圆的方程
思路2
探究新知
待定系数法求切线方方程方法
课堂小结
判断直线与圆的位置关系的方法:
直线与圆公共点的个数
问题3:这节课学习了哪些知识?用到了哪些方法呢?
圆心到直线的距离
方程组实数解的个数
直线与圆的位置关系
定量表达
定性描述
课堂小结
问题3:这节课学习了哪些知识?用到了哪些方法呢?
直线的方程
圆的方程
实数解的个数
x
.
直线与圆的位置关系
代数问题
代数方法
判断直线与圆的位置关系
直线
圆心(),半径r
新知讲解
联立方程组
消去y后得到一个一元二次方程。
方程有一解
直线与圆相切,有一个交点
我们该如何去求切线方程?
随堂检测
1.判断下列各组直线l与圆C的位置关系:
(1) ,;
(2) 圆C:;
(3).
议、展、评
合作探究
2.已知直线与圆心在原点的圆C相切,求圆C的方程.
3.判断直线与圆的位置关系;如果相交,求直线被圆截得的弦长.
习题讲解
解析:设圆C的半径为r ,则,所以圆C的方程为.
小结
如何判断直线与圆的位置关系?
代数法:
方程有两解
直线与圆相交,有两个交点,可通过两点坐标公式求弦长
方程有一解
直线与圆相切,有一个交点
方程有0解
直线与圆相离,无交点
小结
如何判断直线与圆的位置关系?
几何法:
d<r,直线与圆相交,有两个交点
d=r,直线与圆相切,有一个交点
d>r,直线与圆相离,无交点
2.5.1直线与圆的位置关系
第一课时
学习目标
素 养 目 标 学 科 素 养
1.掌握直线与圆的三种位置关系:相交,相切,相离;(重点) 2.会用代数法和几何法来判断直线与圆的三种位置关系;(难点) 3.会用直线与圆的位置关系解决一些实际问题.(重点、难点) 1、直观想象
2、数学运算
3、数形结合
前面我们学习了直线的方程、圆的方程,用直线的方程研究了两条直线的位置关系,本节课我们类比用直线的方程研究两直线位置关系的方法,运用直线与圆的方程,研究直线与圆的的位置关系.
引言
探究新知
探究新知
探究一:用代数方式判断直线与圆的位置关系
相交
相切
相离
.
.
问题1:直线与圆有哪些位置关系?
探究新知
相交
相切
相离
.
.
直线与圆的 位置关系 直线与圆
公共点的个数
相交 2
相切 1
相离 0
.
探究新知
追问1:如何判断直线与圆的位置关系?
追问2:还有其他判断直线与圆的位置关系的方法吗?
.
.
d
∟
d
∟
d
∟
直线与圆位置关系 圆心到直线距
离与半径比较
相交 d
相离 d>r
探究新知
.
.
d
∟
d
∟
d
∟
追问3:判断直线与圆的位置关系有哪些方法?
直线与圆 公共点的个数 直线与圆位置关系 圆心到直线距
离与半径比较
2 相交 d
0 相离 d>r
探究新知
问题2:本章研究直线与圆的方法是什么?
x
y
.
,
()
几何问题
代数问题
几何图形性质
代数方法
探究新知
追问:类比直线与直线的位置关系代数方法,以及根据上述定义,如何利用直线和圆的方程判断它们之间的位置关系?
两直线的位置关系
联立两直线的方程
方程组的解的情况
探究新知
l1 与l2的交点是M(2,2).
追问:类比直线与直线的位置关系代数方法,以及根据上述定义,如何利用直线和圆的方程判断它们之间的位置关系?
两直线的位置关系
联立两直线的方程
方程组解的情况
直线与圆的位置关系
联立直线与
圆的方程
方程组解的情况
探究新知
例题讲解
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
追问1:直线与圆的方程联立组成的方程组,如何判断解的个数?
消去,得,
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
方程有两组实数解
直线与圆相交
例题讲解
方程有一组实数解
直线与圆相切
方程没有实数解
直线与圆相离
代数法:联立方程
例题讲解
解法1:联立直线与圆C的方程,得
消去,得,
解得,.
所以,直线与圆相交,有两个公共点.
把,分别代入方程①,得.
所以,直线与圆C的两个交点是
因此|AB| =.
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
追问2:研究直线与圆的位置关系问题的基本思路是什么?
几何———代数
联立,解方程组
思路1
代数———几何
位置关系
公共点的个数
探究新知
追问3:还有其他方法判断直线与圆的位置关系吗?
几何———代数
求d与r
思路2
代数———几何
位置关系
d
∟
探究新知
d与r的比较
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
例题讲解
解法2:圆C的方程可化为
,
因此圆心C的坐标为(0,1),半径为,
圆心C(0,1)到直线的距离
追问4:如何求圆心到直线的距离?
.
(其中A,B不同时为0)
点P到直线的距离
探究新知
几何法:数形结合
解法2:圆C的方程可化为
,
因此圆心C的坐标为(0,1),半径为,
例1. 已知直线和圆心为C的圆,判断直线与圆的位置关系;如果相交,求直线被圆所截得的弦长.
圆心C(0,1)到直线l的距离
.
所以,直线与圆C相交,有两个公共点.
如图,由垂径定理,得.
例题讲解
判断直线与圆的位置关系的方法
直线与圆相交
直线与圆相切
直线与圆相离
小结:
法1:联立方程
法2:比较d与r
两组解
一组解
无解
d
d>r
探究新知
代数法是直接运用直线和圆的方程组成的方程组有无实数解的情况判断直线与圆的位置关系,是完全代数的方法;具有程序性、普适性.
几何法是利用图形中的相关几何量(圆心到直线的距离、圆的半径)的大小判断直线与圆的位置关系,涉及圆心到直线距离的计算。利用图形的几何性质,有助于简化计算.(数形结合)
代数法与几何法的比较:
探究新知
探究新知
探究二:圆的切线方程
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
P(2,1)
例题讲解
追问1:过圆外一点作圆的切线,能作出几条?
例2 过点作圆的切线,求切线的方程.
追问1:过圆外一点作圆的切线,能作出几条?
x
y
O
P(2,1)
追问2:如何刻画直线与圆相切?
公共点的个数;
圆心到直线的距离
追问3:直线的方程选择什么形式?
点斜式;两点式
例题讲解
过圆外一点可以作圆的两条切线
例题讲解
例2 过点作圆的切线,求切线的方程.
几何法
x
y
O
P(2,1)
点斜式
解法1:
d=r
代数法
解法2:
,
.
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
x=2
解法1:
设切线的斜率为,则切线的方程为
,
因为直线l与圆相切,所以方程组
只有一组解.
例题讲解
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
解法1:
x=2
例题讲解
消元,得.
因为方程①只有一个解,所以
,
解得=0或.
所以,所求切线的方程为=1,或.
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
x=2
解法2:
设切线的斜率为,则切线的方程为
,即.
由圆心(0,0)到切线的距离等于圆的半径1,
得
,解得=0或.
或.
因此,所求切线的方程为y=1
例题讲解
例2 过点作圆的切线,求切线的方程.
x
y
O
P(2,1)
两点式
例题讲解
∟
追问4:你能比较这两种方法的差异吗?
直线与圆相切
直线方程
思路1
直线的方程
圆的方程
思路2
探究新知
待定系数法求切线方方程方法
课堂小结
判断直线与圆的位置关系的方法:
直线与圆公共点的个数
问题3:这节课学习了哪些知识?用到了哪些方法呢?
圆心到直线的距离
方程组实数解的个数
直线与圆的位置关系
定量表达
定性描述
课堂小结
问题3:这节课学习了哪些知识?用到了哪些方法呢?
直线的方程
圆的方程
实数解的个数
x
.
直线与圆的位置关系
代数问题
代数方法
判断直线与圆的位置关系
直线
圆心(),半径r
新知讲解
联立方程组
消去y后得到一个一元二次方程。
方程有一解
直线与圆相切,有一个交点
我们该如何去求切线方程?
随堂检测
1.判断下列各组直线l与圆C的位置关系:
(1) ,;
(2) 圆C:;
(3).
议、展、评
合作探究
2.已知直线与圆心在原点的圆C相切,求圆C的方程.
3.判断直线与圆的位置关系;如果相交,求直线被圆截得的弦长.
习题讲解
解析:设圆C的半径为r ,则,所以圆C的方程为.
小结
如何判断直线与圆的位置关系?
代数法:
方程有两解
直线与圆相交,有两个交点,可通过两点坐标公式求弦长
方程有一解
直线与圆相切,有一个交点
方程有0解
直线与圆相离,无交点
小结
如何判断直线与圆的位置关系?
几何法:
d<r,直线与圆相交,有两个交点
d=r,直线与圆相切,有一个交点
d>r,直线与圆相离,无交点
