数系的扩充和复数的概念(浙江省杭州市富阳市)
文档属性
| 名称 | 数系的扩充和复数的概念(浙江省杭州市富阳市) |

|
|
| 格式 | rar | ||
| 文件大小 | 597.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-01 00:00:00 | ||
图片预览






文档简介
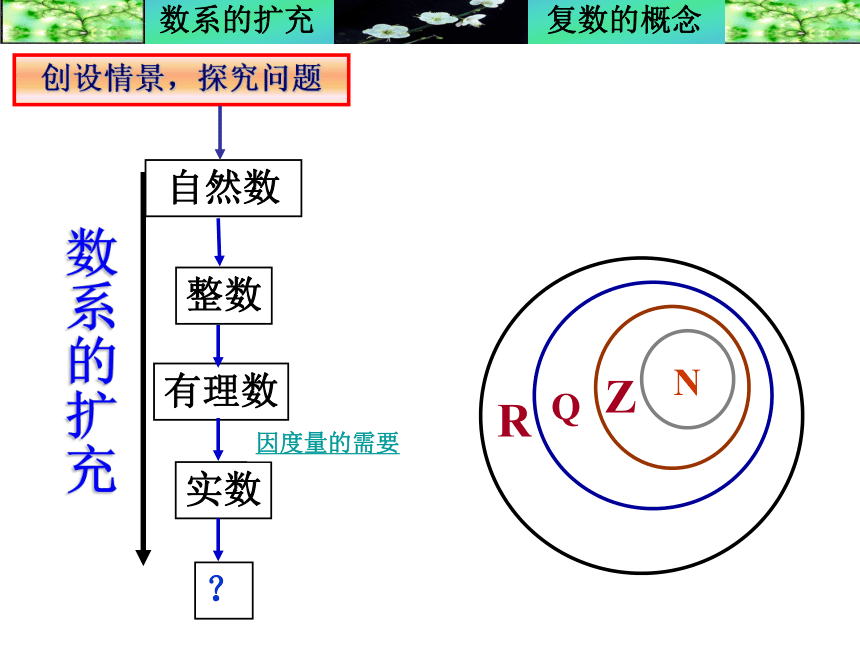
课件20张PPT。数系的扩充与复数的概念课堂组织者:徐敏 时间:2007/10/31场口中学高二数学备课组数系的扩充创设情景,探究问题
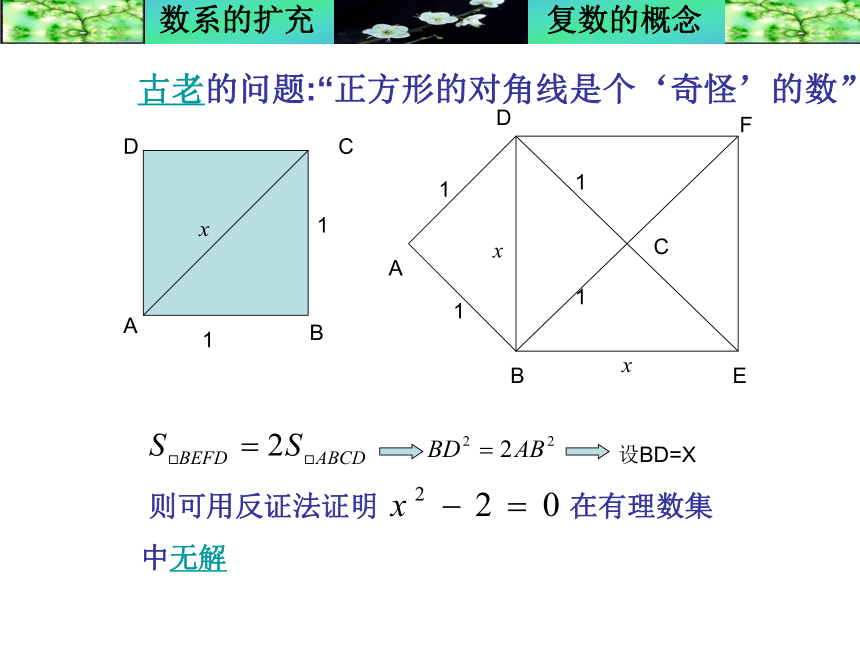
因度量的需要C古老的问题:“正方形的对角线是个‘奇怪’的数”我们知道一元二次方程 x2 +1=0在实数集范围内无解.合情推理,类比扩充
现在我们就引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算率(包括交换率、结合率和分配率)仍然成立。 引入新数,完善数系 ②复数Z=a+bi (a∈R, b∈R )把实数a,b叫做
复数的实部和虚部。1、定义:形如a+bi(a∈R,b∈R)的数叫复数,其中i叫虚数单位。③全体复数所组成的集合叫复数集,记作C。注意:①复数通常用字母z表示,即复数a+bi (a∈R,b∈R)可记作:z =a+bi (a∈R,b∈R),把这一表示形式叫做复数的代数形式。
复数有关概念观察复数的代数形式当a= 0 且b= 0 时,则z=0当b= 0 时,则z为实数
当b ≠0 时,则z为虚数
当a= 0 且b ≠0时,则z为纯虚数
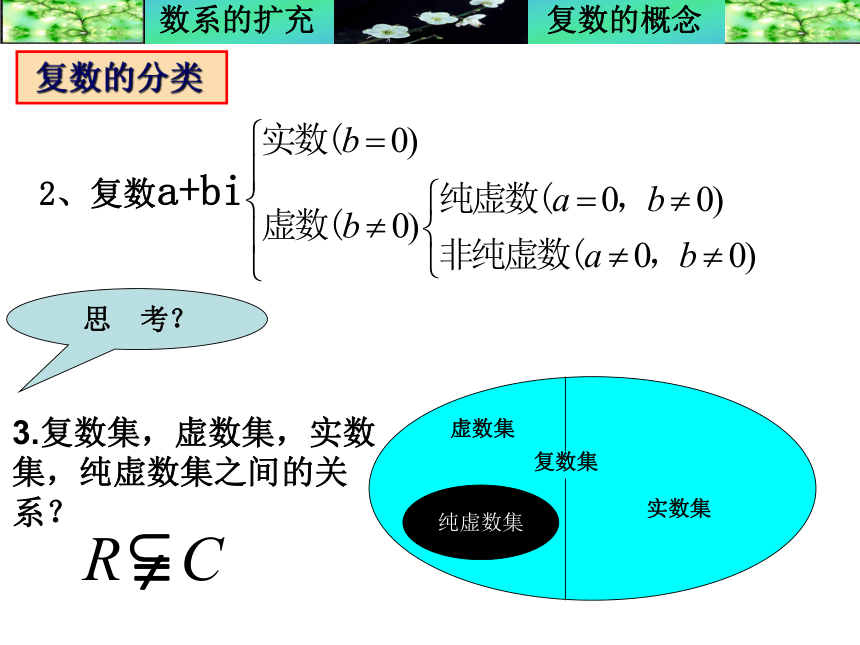
2、复数a+bi3.复数集,虚数集,实数集,纯虚数集之间的关系? 思 考?复数集虚数集实数集纯虚数集 复数的分类1、说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。5 +802、判断下列命题是否正确:
(1)若a、b为实数,则z=a+bi为虚数
(2)若b为实数,则z=bi必为纯虚数
(3)若a为实数,则z= a 一定不是虚数即时训练,巩固新知 典例讲解,变式拓展 变式练习: 实数m取什么值时,复数 z=mi2+1-mi
是(1)实数? (2)虚数? (3)纯虚数?解:(1)当-m =0 ,即m=0 时,复数z 是实数.(2)当 –m≠0 ,即m≠0 时,复数z 是虚数.复数相等的定义 如果两个复数的实部和虚部分别相等,我们就说这两个复数相等. 两个复数不能比较大小,只能由定义判断它们相 等或不相等。
例2 已知 ,其中 求x与y?变式:解题思考:复数相等的问题转化求方程组的解的问题一种重要的数学思想:转化思想变式2、已知两个复数x2-1+(y+1)i大于2x+3+(y2-1)i试求实数x,y的取值范围变式3、已知实数x与纯虚数y满足2x-1
+2i=y,求x,y。
1.虚数单位i的引入;课堂小结作业布置作业本B本上:1、3、5、6、8、9、10再 见关于无理数的发现
古希腊的毕达哥拉斯学派认为, 世间任何数都可以用整数或分数表示,并将此作为他们的一条信条.有一天,这个学派中的一个成员希伯斯突然发现边长为1的正方形的对角线是个奇怪的数,于是努力研究,终于证明出它不能用整数或分数表示.但这打破了毕达哥拉斯学派的信条,于是毕达哥拉斯命令他不许外传.但希伯斯却将这一秘密透露了出去.毕达哥拉斯大怒,要将他处死.希伯斯连忙外逃,然而还是被抓住了,被扔入了大海,为科学的发展献出了宝贵的生命.希伯斯发现的这类数,被称为无理数.无理数的发现,导致了第一次数学危机,为数学的发展做出了重大贡献.
数系的扩充创设情景,探究问题因计数的需要因不够减的需要,引入负数
因测量、分配中的等分问题引入分数
(分数集?有理数集?循环小数集)
实数集?小数集?
因度量的需要 提出问题:根据前面数系扩充的资料你能设想一种方法,使方程x2 + 1 =0有解吗?提示:每一次数的扩充都是在遇到了用原有的数系不能表示所要解决的问题时,引入新数来表示新的问题的。
合情推理,类比扩充
因度量的需要C古老的问题:“正方形的对角线是个‘奇怪’的数”我们知道一元二次方程 x2 +1=0在实数集范围内无解.合情推理,类比扩充
现在我们就引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算率(包括交换率、结合率和分配率)仍然成立。 引入新数,完善数系 ②复数Z=a+bi (a∈R, b∈R )把实数a,b叫做
复数的实部和虚部。1、定义:形如a+bi(a∈R,b∈R)的数叫复数,其中i叫虚数单位。③全体复数所组成的集合叫复数集,记作C。注意:①复数通常用字母z表示,即复数a+bi (a∈R,b∈R)可记作:z =a+bi (a∈R,b∈R),把这一表示形式叫做复数的代数形式。
复数有关概念观察复数的代数形式当a= 0 且b= 0 时,则z=0当b= 0 时,则z为实数
当b ≠0 时,则z为虚数
当a= 0 且b ≠0时,则z为纯虚数
2、复数a+bi3.复数集,虚数集,实数集,纯虚数集之间的关系? 思 考?复数集虚数集实数集纯虚数集 复数的分类1、说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。5 +802、判断下列命题是否正确:
(1)若a、b为实数,则z=a+bi为虚数
(2)若b为实数,则z=bi必为纯虚数
(3)若a为实数,则z= a 一定不是虚数即时训练,巩固新知 典例讲解,变式拓展 变式练习: 实数m取什么值时,复数 z=mi2+1-mi
是(1)实数? (2)虚数? (3)纯虚数?解:(1)当-m =0 ,即m=0 时,复数z 是实数.(2)当 –m≠0 ,即m≠0 时,复数z 是虚数.复数相等的定义 如果两个复数的实部和虚部分别相等,我们就说这两个复数相等. 两个复数不能比较大小,只能由定义判断它们相 等或不相等。
例2 已知 ,其中 求x与y?变式:解题思考:复数相等的问题转化求方程组的解的问题一种重要的数学思想:转化思想变式2、已知两个复数x2-1+(y+1)i大于2x+3+(y2-1)i试求实数x,y的取值范围变式3、已知实数x与纯虚数y满足2x-1
+2i=y,求x,y。
1.虚数单位i的引入;课堂小结作业布置作业本B本上:1、3、5、6、8、9、10再 见关于无理数的发现
古希腊的毕达哥拉斯学派认为, 世间任何数都可以用整数或分数表示,并将此作为他们的一条信条.有一天,这个学派中的一个成员希伯斯突然发现边长为1的正方形的对角线是个奇怪的数,于是努力研究,终于证明出它不能用整数或分数表示.但这打破了毕达哥拉斯学派的信条,于是毕达哥拉斯命令他不许外传.但希伯斯却将这一秘密透露了出去.毕达哥拉斯大怒,要将他处死.希伯斯连忙外逃,然而还是被抓住了,被扔入了大海,为科学的发展献出了宝贵的生命.希伯斯发现的这类数,被称为无理数.无理数的发现,导致了第一次数学危机,为数学的发展做出了重大贡献.
数系的扩充创设情景,探究问题因计数的需要因不够减的需要,引入负数
因测量、分配中的等分问题引入分数
(分数集?有理数集?循环小数集)
实数集?小数集?
因度量的需要 提出问题:根据前面数系扩充的资料你能设想一种方法,使方程x2 + 1 =0有解吗?提示:每一次数的扩充都是在遇到了用原有的数系不能表示所要解决的问题时,引入新数来表示新的问题的。
合情推理,类比扩充
