第四单元长方体(二)(A卷知识通关练)2023-2024年五年级下册(北师大版)(含答案)
文档属性
| 名称 | 第四单元长方体(二)(A卷知识通关练)2023-2024年五年级下册(北师大版)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 58.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 15:32:21 | ||
图片预览




文档简介
第四单元 长方体(二)(A卷 知识通关练)
一、填空题(30分)
1.一个正方体的棱长总和是48厘米,它的体积是( )立方厘米。
2.一个正方体的棱长扩大到原来的2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
3.用一根48厘米长的铁丝焊成一个正方体,这个正方体的表面积是( )平方厘米,体积是( )立方厘米。
4.有一根长方体木料体积是630dm3,它的截面面积是70dm2,这根木料的长应是( )。
5.20000毫升=( )升 8升=( )毫升 ( )毫升>4升
6.某品牌汽车油箱的长是50cm,宽是40cm,高是30cm,这个油箱能装( )升汽油。如果每升汽油可行驶12km,这箱油最多可供这辆汽车行驶( )千米。
7.组成下面各图的小正方体是1cm3,把每个图形的体积写在括号里。
( ) ( ) ( )
8.把一个长是6厘米,宽是5厘米,高是4厘米的长方体加工成一个最大的正方体,这个正方体的体积是 立方厘米。
二、选择题(20分)
9.一个正方体的棱长扩大到3倍,它的体积扩大到( )倍。
A.3 B.6 C.9 D.27
10.求做一个长方体灯箱需要多少平方米灯箱布(接头不计),是求长方体灯箱的( )。
A.表面积 B.体积 C.容积 D.不能确定
11.用两个同样大小的小正方体拼成一个长方体后,下面说法正确的是( )。
A.体积不变,表面积变小 B.体积不变,表面积变大
C.表面积不变,体积变小 D.表面积不变,体积变大
12.棱长8cm的正方体与一个长方体的体积相等。已知长方体的高是16cm,那么它的底面积是( )cm2。
A.0.5 B.128 C.32 D.64
13.在长8m、宽2.6m、高3m的集装箱中摆放棱长是8dm的正方体货箱,最多能摆( )个。
A.9 B.90 C.121 D.122
14.下列物体中体积约为1000cm3的是( )。
A.一盒粉笔 B.20本数学书 C.一台电视机 D.一部智能手机
15.边长是6dm的正方体,它的表面积与体积比较( )。
A.一样大 B.表面积大 C.不能比较大小 D.体积大
16.一种水箱最多可装水65升,我们就说这种水箱的( )是65升。
A.底面积 B.表面积 C.容积 D.质量
17.把一盒1.5升的果汁倒进容积为250毫升的杯子里,能倒满( )杯。
A.0.6 B.6 C.60 D.600
18.爸爸在一个长8dm,宽5dm,高4dm的长方体鱼缸中放入一个假山石(完全浸没),水面上升了3cm,这个假山石的体积是( )。
A.16cm3 B.120dm3 C.120cm3 D.12dm3
三、判断题(10分)
19.棱长为6dm的正方体的体积和表面积相等。( )
20.正方体的棱长扩大到原来的3倍,体积就扩大到原来的9倍。( )
21.棱长是6厘米的正方体的表面积和体积相等。( )
22.长方体中,底面积越大,体积也越大。( )。
23.两个体积一样的大盒子,它们的容积一定同样大。( )
四、排序题(按从小到大的顺序排列)。(5分)
24.按从小到大的顺序排列。
( )<( )<( )<( )<( )
五、图形计算(8分)
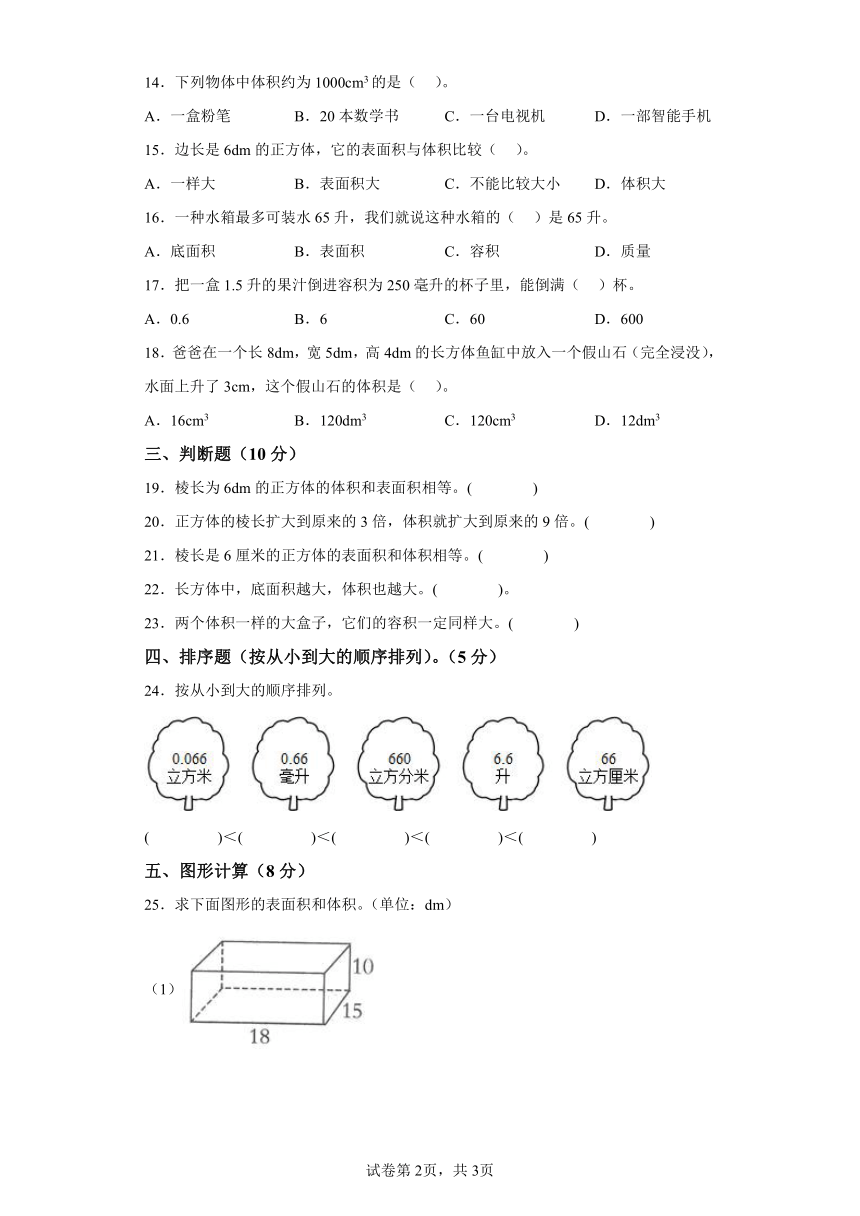
25.求下面图形的表面积和体积。(单位:dm)
(1)
(2)
六、解答题(27分)
26.学校运来7.6立方米的沙子,铺在一个长5米,宽38分米的沙坑里,可以铺多厚?
27.一根长1米的长方体木料锯成2段后,表面积增加了60平方厘米。这根木料的体积是多少立方厘米?
28.一个长方体的汽油桶,底面积是30平方分米,高是6分米。如果1升汽油重0.7千克,这个油桶可以装多少千克汽油?
29.一块长方体钢材,长30分米,宽6分米,高5分米,如果每立方分米钢材重7.8千克,这块钢材的质量是多少吨?
30.一个长方体水槽槽内长1.2米,宽60厘米,深50厘米。这个水槽容积是多少毫升?合多少升?
试卷第2页,共3页
试卷第3页,共3页
参考答案:
1.64
【分析】根据正方体的特征,正方体有12条棱,并且每条棱长度相等,用已知的48厘米除以12即可算出每条棱的长度,再根据正方体体积公式:V=棱长×棱长×棱长,代入数据求值即可。
【详解】由分析可得:
棱长为:48÷12=4(厘米)
体积为:
4×4×4
=16×4
=64(立方厘米)
【点睛】本题考查了对正方体特征的认识以及对正方体体积公式的掌握,需要学生熟悉正方体12条棱的特点。
2. 4 8
【分析】一个正方体的棱长扩大到原来的几倍,表面积扩大到原来的倍数×倍数,体积扩大到原来的倍数×倍数×倍数,据此分析。
【详解】2×2=4
2×2×2=8
【点睛】关键是掌握正方体表面积和体积公式,正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长。
3. 96 64
【分析】依据正方体的棱长总和=棱长×12,可得正方体棱长,即:48÷12=4(厘米);然后根据正方体表面积=棱长×棱长×6,再根据正方体体积=棱长×棱长×棱长进行计算。
【详解】48÷12=4(厘米)
4×4×6=96(平方厘米)
4×4×4=64(立方厘米)。
【点睛】本题考查正方体的表面积和体积,熟练掌握正方体的表面积和体积计算方法是解题关键。
4.9分米
【分析】由题意知:长方体的体积已知,截面面积已知,用体积除以截面面积即是长方体的高(本题指的是长),据此解答。
【详解】630÷70=9(分米)
【点睛】本题考查了对长方体体积公式的灵活运用。掌握长方体的体积公式是解答本题的关键。
5. 20 8000 4001
【分析】(1)低级单位毫升化高级单位升除以进率1000;
(2)高级单位升化低级单位毫升乘进率1000;
(3)此题答案不唯一,4升=4000毫升,只要填大于4000的数均可。
【详解】(1)20000毫升=20升;(2)8升=8000毫升;(3)4001毫升>4升
【点睛】升与毫升之间的进率是1000,由高级单位化低级单位乘进率,反之除以进率。
6. 60 720
【分析】根据长方体的体积(容积)公式:V=abh,把数据代入公式求出这个油箱能装多少升汽油,然后根据乘法的意义,用每升汽油行驶的里程乘这箱汽油的体积即可。
【详解】50×40×30
=2000×30
=60000(立方厘米)
60000立方厘米=60升
12×60=720(千米)
【点睛】此题主要考查长方体的体积(容积)公式的灵活运用,关键是熟记公式。
7. 5立方厘米 5立方厘米 6立方厘米
【分析】因为一个小正方体的体积是1立方厘米,数出每个立方体的个数,是几个就是几立方厘米;由此解答即可。
【详解】
【点睛】此题考查了体积、容积及其单位,明确一个小正方体的体积是1立方厘米,数出个数是解答此题的关键。
8.64
【分析】把这个长方体加工成一个最大的正方体,即这个正方体的棱长和长方体的最短的一个棱相等,所以这个正方体的棱长与长方体的高相等,正方体的体积公式是v=a3,直接列式解答。
【详解】4×4×4
=16×4
=64(立方厘米),
【点睛】此题主要考查正方体的体积计算,关键是清楚把这个长方体切削乘一个最大的正方体,此时正方体的棱长是多少。
9.D
【分析】正方体体积=棱长×棱长×棱长,所以,一个正方体的棱长扩大到3倍,它的体积扩大到(3×3×3)倍。
【详解】3×3×3=27倍
所以,一个正方体的棱长扩大到3倍,它的体积扩大到27倍。
故答案为:D
【点睛】本题考查了正方体的体积,解题关键是熟记体积公式。
10.A
【分析】解答这类问题首先要搞清所求物体的形状,因为是求做一个长方体灯箱需要多少平方米灯箱布,根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等,所以是求长方体的表面积。
【详解】根据灯箱的形状和它的用途,所以求做一个长方体灯箱需要多少平方米灯箱布,是求长方体灯箱的表面积。
故答案为:A
【点睛】解答这类问题首先要搞清所求物体的形状,再根据题意来确定选项。
11.A
【分析】把两个完全一样的正方体拼成一个长方体后,减少了两个正方形的面,所以表面积减少,但体积没有变化。据此解答。
【详解】由分析知:两个同样大小的小正方体拼成一个长方体后,体积不变,表面积变小。
故答案为:A
【点睛】本题考查立体图形的切拼。根据立体图形表面积和体积的意义进行分析。
12.C
【分析】先计算出正方体的体积,根据“底面积=体积÷高”即可解答。
【详解】(8×8×8)÷16
=512÷16
=32(cm2)
故答案为:C
【点睛】灵活运用长方体的体积公式是解答本题的关键。
13.B
【分析】分别求出长方体的长、宽、高各包含正方体棱长的个数,就是说长、宽、高中最多有多少个正方体的棱长,再将长、宽、高包含的正方体的棱长个数相乘,即可解答。
【详解】8米=80分米;2.6米=26分米;3米=30分米
80÷8=10(个)
26÷8=3(个)……2(分米)
30÷8=3(个)……6(分米)
最多可装正方体货箱个数:
10×3×3
=30×3
=90(个)
故答案选:B
【点睛】本题考查长方体、正方体体积的计算的应用,关键是单位名数的互换,以及取整数。
14.A
【分析】1000立方厘米=1立方分米,结合生活实际找出体积约是1立方分米的物体即可。
【详解】A. 一盒粉笔的体积约是1立方分米,符合题意。
B.20本数学书的体积远大于1立方分米,不符合题意。
C.一台电视机的体积远大于1立方分米,不符合题意。
D.一部智能手机的体积明显小于1立方分米,不符合题意。
故选择:A
【点睛】此题考查了对体积单位大小的认识,能够感知单位体积的大小是解题关键。
15.C
【分析】根据正方体的表面积意义和体积的意义进行解答。
【详解】正方体的表面积是指组成它的所有面的面积和;体积是指它所占空间的大小;二者意义不一样,不能比较大小,所以边长是6dm的正方体,它的表面积与体积不能进行比较。
故答案为:C
【点睛】本题考查正方体的表面积和体积的意义。
16.C
【分析】体积是物体所占空间的大小,容积就是指容器所能容纳物体的体积,占地面积是物体底面所占面积的大小,表面积是物体表面面积的和;据此即可做出正确选择。
【详解】A.占地面积是物体底面所占面积的大小,所以A错误;
B.表面积是物体表面面积的和,所以B错误;
C.因为体积是物体所占空间的大小,容积就是指容器所能容纳物体的体积,所以C正确
D.质量是物体所具有的一种物理属性,是物质的量的量度,所以D错误。
故答案为:C。
【点睛】正确区分容积、底面积、表面积、质量等概念是解决此题的关键。
17.B
【分析】把1.5升乘进率1000化成1500毫升,就是求1500毫升里面有多少个250毫升,根据包含除法的意义,用1500毫升除以250毫升。
【详解】1.5升=1500毫升
1500÷250=6(杯)
故答案为:B。
【点睛】把这盒果汁的体积、杯子的容积,化成相同单位的名数,再根据包含除法的意义即可解答。
18.D
【分析】根据题意即可分析,假山石的体积就等于水面上升了3cm的水体积,而水面上升了3cm的水的体积就可以理解为是长8dm、宽5dm、高为3cm的长方体的体积,此时再依据长方体的体积公式即可求得,注意要换算单位。
【详解】3cm=0.3dm
8×5×0.3=12(dm3)
故答案为:D
【点睛】此题关键在于灵活运用转化策略,将不规则物体的体积转化为求规则物体的体积,但要注意计算时单位不同时,一定要先统一单位。
19.×
【分析】物体所有面的总面积叫做物体的表面积;物体所占空间的大小叫做物体的体积。
【详解】表面积与体积的意义不同,是不同类量,无法比较大小。
棱长为6dm的正方体的体积和表面积不能比较大小。
原题说法错误。
故答案为:×
【点睛】本题考查正方体的表面积、体积的意义,明确只有同类量才能比较大小。
20.×
【分析】正方体的体积=棱长×棱长×棱长,正方体的棱长扩大到原来的3倍,体积就扩大到原来的3×3×3=27倍,据此判断即可。
【详解】由分析可知:正方体的棱长扩大到原来的3倍,体积就扩大到原来的27倍,原题说法错误。
故答案为:×
【点睛】掌握正方体的体积公式是解答本题的关键。
21.×
【分析】表面积表示立体图形各个面的面积之和,而体积表示物体所占空间的大小,正方体的表面积和体积的单位不相同,没法比较它们的大小。据此判断。
【详解】表面积:6×6×6=216(平方厘米)
体积:6×6×6=216(立方厘米)
这个正方体的表面积和体积从数值上看是相等的,但是两个数的单位不相同,不能比较大小。
故答案为:×
【点睛】此题主要考查正方体的表面积和体积的意义,表面积和体积是两个完全不同的概念,不能比较大小。
22.×
【分析】根据长方体体积公式:长方体体积=底面积×高;由此可知,长方体的体积大小是由底面积和高共同决定的,据此解答。
【详解】根据分析可知,长方体的体积大小是由底面积和高决定的。
原题干说的错误。
故答案为:×
【点睛】本题考查长方体体积公式的应用,关键是熟记公式,灵活运用。
23.×
【分析】容积是指物体所容纳物体的体积,两个体积一样大的盒子,盒皮的厚度不一样,所容纳物体的体积就不一样,盒皮厚的容纳的体积少些,盒皮薄的容纳的体积多些,如果厚度一样,容积就一样大,据此解答即可。
【详解】两个体积一样大的盒子,它们的容积一定同样大的说法是错误的,应该是容积不一定同样大。
故答案为:×
【点睛】此题考查容积的意义,解决此题的关键是容积的定义,注重盒皮的厚度。
24. 0.66毫升 66立方厘米 6.6升 0.066立方米 660立方分米
【详解】略
25.(1)表面积:1200dm2;体积:2700dm3
(2)表面积:384dm2;体积:512dm3
【分析】(1)根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,求出表面积;根据长方体体积公式:长×宽×高,代入数据,即可解答;
(2)根据正方体表面积公式:棱长×棱长×6,代入数据,求出表面积;根据正方体体积公式:棱长×棱长×棱长,代入数据,即可解答。
【详解】(1)表面积:
(18×15+18×10+15×10)×2
=(270+180+150)×2
=(450+150)×2
=600×2
=1200(dm2)
体积:
18×15×10
=270×10
=2700(dm3)
(2)表面积:8×8×6
=64×6
=384(dm2)
体积:
8×8×8
=64×8
=512(dm3)
26.0.4米
【分析】由“长方体的体积=长×宽×高”可知,高=长方体的体积÷长÷宽,把题中数据代入公式求出这些沙子可以铺的厚度,据此解答。
【详解】38分米=3.8米
7.6÷5÷3.8
=1.52÷3.8
=0.4(米)
答:可以铺0.4米厚。
【点睛】本题主要考查长方体体积公式的应用,灵活运用公式是解答题目的关键。
27.3000cm3
【分析】截成2段后,表面积比原来增加了2个横截面的面积,因为表面积是增加了60平方厘米,由此即可求出横截面的面积是60÷2=30平方厘米,由此再乘以长就是这根木料的体积。
【详解】1米=100厘米
60÷2×100
=30×100
=3000(立方厘米)
答:这根木料的体积是3000立方厘米。
【点睛】抓住长方体的切割特点和增加的表面积求出长方体的横截面的面积是解决此题的关键。
28.126千克
【分析】根据长方体的体积=底面积×高,求出汽油桶的容积,乘每升汽油的重量即可。
【详解】30×6×0.7
=180×0.7
=126(千克)
答:这个油桶可以装126千克汽油。
【点睛】此题主要考查了长方体容积的相关应用,先求出汽油桶的容积是解题关键。
29.7.02吨
【分析】根据“长方体体积=长×宽×高”求出长方体钢材的体积,再乘每立方分米钢材的质量即可。
【详解】30×6×5×7.8
=900×7.8
=7020(千克)
7020千克=7.02吨
答:这块钢材的质量是7.02吨。
【点睛】熟练掌握长方体的体积计算公式是解答本题的关键。
30.360000毫升;360升
【分析】容积为物体所能容纳物体的体积,统一单位,将1.2米转化为120厘米。 水槽的容积=长方体的体积=长×宽×高,据此代入数据求出容积。
【详解】1.2米=120厘米
120×60×50
=7200×50
=360000(立方厘米)
360000立方厘米=360000毫升=360升
答:这个水槽容积是360000毫升。合360升。
【点睛】此题考查了长方体容积的计算,注意升与毫升进率是1000。
答案第2页,共9页
答案第3页,共9页
一、填空题(30分)
1.一个正方体的棱长总和是48厘米,它的体积是( )立方厘米。
2.一个正方体的棱长扩大到原来的2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
3.用一根48厘米长的铁丝焊成一个正方体,这个正方体的表面积是( )平方厘米,体积是( )立方厘米。
4.有一根长方体木料体积是630dm3,它的截面面积是70dm2,这根木料的长应是( )。
5.20000毫升=( )升 8升=( )毫升 ( )毫升>4升
6.某品牌汽车油箱的长是50cm,宽是40cm,高是30cm,这个油箱能装( )升汽油。如果每升汽油可行驶12km,这箱油最多可供这辆汽车行驶( )千米。
7.组成下面各图的小正方体是1cm3,把每个图形的体积写在括号里。
( ) ( ) ( )
8.把一个长是6厘米,宽是5厘米,高是4厘米的长方体加工成一个最大的正方体,这个正方体的体积是 立方厘米。
二、选择题(20分)
9.一个正方体的棱长扩大到3倍,它的体积扩大到( )倍。
A.3 B.6 C.9 D.27
10.求做一个长方体灯箱需要多少平方米灯箱布(接头不计),是求长方体灯箱的( )。
A.表面积 B.体积 C.容积 D.不能确定
11.用两个同样大小的小正方体拼成一个长方体后,下面说法正确的是( )。
A.体积不变,表面积变小 B.体积不变,表面积变大
C.表面积不变,体积变小 D.表面积不变,体积变大
12.棱长8cm的正方体与一个长方体的体积相等。已知长方体的高是16cm,那么它的底面积是( )cm2。
A.0.5 B.128 C.32 D.64
13.在长8m、宽2.6m、高3m的集装箱中摆放棱长是8dm的正方体货箱,最多能摆( )个。
A.9 B.90 C.121 D.122
14.下列物体中体积约为1000cm3的是( )。
A.一盒粉笔 B.20本数学书 C.一台电视机 D.一部智能手机
15.边长是6dm的正方体,它的表面积与体积比较( )。
A.一样大 B.表面积大 C.不能比较大小 D.体积大
16.一种水箱最多可装水65升,我们就说这种水箱的( )是65升。
A.底面积 B.表面积 C.容积 D.质量
17.把一盒1.5升的果汁倒进容积为250毫升的杯子里,能倒满( )杯。
A.0.6 B.6 C.60 D.600
18.爸爸在一个长8dm,宽5dm,高4dm的长方体鱼缸中放入一个假山石(完全浸没),水面上升了3cm,这个假山石的体积是( )。
A.16cm3 B.120dm3 C.120cm3 D.12dm3
三、判断题(10分)
19.棱长为6dm的正方体的体积和表面积相等。( )
20.正方体的棱长扩大到原来的3倍,体积就扩大到原来的9倍。( )
21.棱长是6厘米的正方体的表面积和体积相等。( )
22.长方体中,底面积越大,体积也越大。( )。
23.两个体积一样的大盒子,它们的容积一定同样大。( )
四、排序题(按从小到大的顺序排列)。(5分)
24.按从小到大的顺序排列。
( )<( )<( )<( )<( )
五、图形计算(8分)
25.求下面图形的表面积和体积。(单位:dm)
(1)
(2)
六、解答题(27分)
26.学校运来7.6立方米的沙子,铺在一个长5米,宽38分米的沙坑里,可以铺多厚?
27.一根长1米的长方体木料锯成2段后,表面积增加了60平方厘米。这根木料的体积是多少立方厘米?
28.一个长方体的汽油桶,底面积是30平方分米,高是6分米。如果1升汽油重0.7千克,这个油桶可以装多少千克汽油?
29.一块长方体钢材,长30分米,宽6分米,高5分米,如果每立方分米钢材重7.8千克,这块钢材的质量是多少吨?
30.一个长方体水槽槽内长1.2米,宽60厘米,深50厘米。这个水槽容积是多少毫升?合多少升?
试卷第2页,共3页
试卷第3页,共3页
参考答案:
1.64
【分析】根据正方体的特征,正方体有12条棱,并且每条棱长度相等,用已知的48厘米除以12即可算出每条棱的长度,再根据正方体体积公式:V=棱长×棱长×棱长,代入数据求值即可。
【详解】由分析可得:
棱长为:48÷12=4(厘米)
体积为:
4×4×4
=16×4
=64(立方厘米)
【点睛】本题考查了对正方体特征的认识以及对正方体体积公式的掌握,需要学生熟悉正方体12条棱的特点。
2. 4 8
【分析】一个正方体的棱长扩大到原来的几倍,表面积扩大到原来的倍数×倍数,体积扩大到原来的倍数×倍数×倍数,据此分析。
【详解】2×2=4
2×2×2=8
【点睛】关键是掌握正方体表面积和体积公式,正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长。
3. 96 64
【分析】依据正方体的棱长总和=棱长×12,可得正方体棱长,即:48÷12=4(厘米);然后根据正方体表面积=棱长×棱长×6,再根据正方体体积=棱长×棱长×棱长进行计算。
【详解】48÷12=4(厘米)
4×4×6=96(平方厘米)
4×4×4=64(立方厘米)。
【点睛】本题考查正方体的表面积和体积,熟练掌握正方体的表面积和体积计算方法是解题关键。
4.9分米
【分析】由题意知:长方体的体积已知,截面面积已知,用体积除以截面面积即是长方体的高(本题指的是长),据此解答。
【详解】630÷70=9(分米)
【点睛】本题考查了对长方体体积公式的灵活运用。掌握长方体的体积公式是解答本题的关键。
5. 20 8000 4001
【分析】(1)低级单位毫升化高级单位升除以进率1000;
(2)高级单位升化低级单位毫升乘进率1000;
(3)此题答案不唯一,4升=4000毫升,只要填大于4000的数均可。
【详解】(1)20000毫升=20升;(2)8升=8000毫升;(3)4001毫升>4升
【点睛】升与毫升之间的进率是1000,由高级单位化低级单位乘进率,反之除以进率。
6. 60 720
【分析】根据长方体的体积(容积)公式:V=abh,把数据代入公式求出这个油箱能装多少升汽油,然后根据乘法的意义,用每升汽油行驶的里程乘这箱汽油的体积即可。
【详解】50×40×30
=2000×30
=60000(立方厘米)
60000立方厘米=60升
12×60=720(千米)
【点睛】此题主要考查长方体的体积(容积)公式的灵活运用,关键是熟记公式。
7. 5立方厘米 5立方厘米 6立方厘米
【分析】因为一个小正方体的体积是1立方厘米,数出每个立方体的个数,是几个就是几立方厘米;由此解答即可。
【详解】
【点睛】此题考查了体积、容积及其单位,明确一个小正方体的体积是1立方厘米,数出个数是解答此题的关键。
8.64
【分析】把这个长方体加工成一个最大的正方体,即这个正方体的棱长和长方体的最短的一个棱相等,所以这个正方体的棱长与长方体的高相等,正方体的体积公式是v=a3,直接列式解答。
【详解】4×4×4
=16×4
=64(立方厘米),
【点睛】此题主要考查正方体的体积计算,关键是清楚把这个长方体切削乘一个最大的正方体,此时正方体的棱长是多少。
9.D
【分析】正方体体积=棱长×棱长×棱长,所以,一个正方体的棱长扩大到3倍,它的体积扩大到(3×3×3)倍。
【详解】3×3×3=27倍
所以,一个正方体的棱长扩大到3倍,它的体积扩大到27倍。
故答案为:D
【点睛】本题考查了正方体的体积,解题关键是熟记体积公式。
10.A
【分析】解答这类问题首先要搞清所求物体的形状,因为是求做一个长方体灯箱需要多少平方米灯箱布,根据长方体的特征,6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等,所以是求长方体的表面积。
【详解】根据灯箱的形状和它的用途,所以求做一个长方体灯箱需要多少平方米灯箱布,是求长方体灯箱的表面积。
故答案为:A
【点睛】解答这类问题首先要搞清所求物体的形状,再根据题意来确定选项。
11.A
【分析】把两个完全一样的正方体拼成一个长方体后,减少了两个正方形的面,所以表面积减少,但体积没有变化。据此解答。
【详解】由分析知:两个同样大小的小正方体拼成一个长方体后,体积不变,表面积变小。
故答案为:A
【点睛】本题考查立体图形的切拼。根据立体图形表面积和体积的意义进行分析。
12.C
【分析】先计算出正方体的体积,根据“底面积=体积÷高”即可解答。
【详解】(8×8×8)÷16
=512÷16
=32(cm2)
故答案为:C
【点睛】灵活运用长方体的体积公式是解答本题的关键。
13.B
【分析】分别求出长方体的长、宽、高各包含正方体棱长的个数,就是说长、宽、高中最多有多少个正方体的棱长,再将长、宽、高包含的正方体的棱长个数相乘,即可解答。
【详解】8米=80分米;2.6米=26分米;3米=30分米
80÷8=10(个)
26÷8=3(个)……2(分米)
30÷8=3(个)……6(分米)
最多可装正方体货箱个数:
10×3×3
=30×3
=90(个)
故答案选:B
【点睛】本题考查长方体、正方体体积的计算的应用,关键是单位名数的互换,以及取整数。
14.A
【分析】1000立方厘米=1立方分米,结合生活实际找出体积约是1立方分米的物体即可。
【详解】A. 一盒粉笔的体积约是1立方分米,符合题意。
B.20本数学书的体积远大于1立方分米,不符合题意。
C.一台电视机的体积远大于1立方分米,不符合题意。
D.一部智能手机的体积明显小于1立方分米,不符合题意。
故选择:A
【点睛】此题考查了对体积单位大小的认识,能够感知单位体积的大小是解题关键。
15.C
【分析】根据正方体的表面积意义和体积的意义进行解答。
【详解】正方体的表面积是指组成它的所有面的面积和;体积是指它所占空间的大小;二者意义不一样,不能比较大小,所以边长是6dm的正方体,它的表面积与体积不能进行比较。
故答案为:C
【点睛】本题考查正方体的表面积和体积的意义。
16.C
【分析】体积是物体所占空间的大小,容积就是指容器所能容纳物体的体积,占地面积是物体底面所占面积的大小,表面积是物体表面面积的和;据此即可做出正确选择。
【详解】A.占地面积是物体底面所占面积的大小,所以A错误;
B.表面积是物体表面面积的和,所以B错误;
C.因为体积是物体所占空间的大小,容积就是指容器所能容纳物体的体积,所以C正确
D.质量是物体所具有的一种物理属性,是物质的量的量度,所以D错误。
故答案为:C。
【点睛】正确区分容积、底面积、表面积、质量等概念是解决此题的关键。
17.B
【分析】把1.5升乘进率1000化成1500毫升,就是求1500毫升里面有多少个250毫升,根据包含除法的意义,用1500毫升除以250毫升。
【详解】1.5升=1500毫升
1500÷250=6(杯)
故答案为:B。
【点睛】把这盒果汁的体积、杯子的容积,化成相同单位的名数,再根据包含除法的意义即可解答。
18.D
【分析】根据题意即可分析,假山石的体积就等于水面上升了3cm的水体积,而水面上升了3cm的水的体积就可以理解为是长8dm、宽5dm、高为3cm的长方体的体积,此时再依据长方体的体积公式即可求得,注意要换算单位。
【详解】3cm=0.3dm
8×5×0.3=12(dm3)
故答案为:D
【点睛】此题关键在于灵活运用转化策略,将不规则物体的体积转化为求规则物体的体积,但要注意计算时单位不同时,一定要先统一单位。
19.×
【分析】物体所有面的总面积叫做物体的表面积;物体所占空间的大小叫做物体的体积。
【详解】表面积与体积的意义不同,是不同类量,无法比较大小。
棱长为6dm的正方体的体积和表面积不能比较大小。
原题说法错误。
故答案为:×
【点睛】本题考查正方体的表面积、体积的意义,明确只有同类量才能比较大小。
20.×
【分析】正方体的体积=棱长×棱长×棱长,正方体的棱长扩大到原来的3倍,体积就扩大到原来的3×3×3=27倍,据此判断即可。
【详解】由分析可知:正方体的棱长扩大到原来的3倍,体积就扩大到原来的27倍,原题说法错误。
故答案为:×
【点睛】掌握正方体的体积公式是解答本题的关键。
21.×
【分析】表面积表示立体图形各个面的面积之和,而体积表示物体所占空间的大小,正方体的表面积和体积的单位不相同,没法比较它们的大小。据此判断。
【详解】表面积:6×6×6=216(平方厘米)
体积:6×6×6=216(立方厘米)
这个正方体的表面积和体积从数值上看是相等的,但是两个数的单位不相同,不能比较大小。
故答案为:×
【点睛】此题主要考查正方体的表面积和体积的意义,表面积和体积是两个完全不同的概念,不能比较大小。
22.×
【分析】根据长方体体积公式:长方体体积=底面积×高;由此可知,长方体的体积大小是由底面积和高共同决定的,据此解答。
【详解】根据分析可知,长方体的体积大小是由底面积和高决定的。
原题干说的错误。
故答案为:×
【点睛】本题考查长方体体积公式的应用,关键是熟记公式,灵活运用。
23.×
【分析】容积是指物体所容纳物体的体积,两个体积一样大的盒子,盒皮的厚度不一样,所容纳物体的体积就不一样,盒皮厚的容纳的体积少些,盒皮薄的容纳的体积多些,如果厚度一样,容积就一样大,据此解答即可。
【详解】两个体积一样大的盒子,它们的容积一定同样大的说法是错误的,应该是容积不一定同样大。
故答案为:×
【点睛】此题考查容积的意义,解决此题的关键是容积的定义,注重盒皮的厚度。
24. 0.66毫升 66立方厘米 6.6升 0.066立方米 660立方分米
【详解】略
25.(1)表面积:1200dm2;体积:2700dm3
(2)表面积:384dm2;体积:512dm3
【分析】(1)根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,求出表面积;根据长方体体积公式:长×宽×高,代入数据,即可解答;
(2)根据正方体表面积公式:棱长×棱长×6,代入数据,求出表面积;根据正方体体积公式:棱长×棱长×棱长,代入数据,即可解答。
【详解】(1)表面积:
(18×15+18×10+15×10)×2
=(270+180+150)×2
=(450+150)×2
=600×2
=1200(dm2)
体积:
18×15×10
=270×10
=2700(dm3)
(2)表面积:8×8×6
=64×6
=384(dm2)
体积:
8×8×8
=64×8
=512(dm3)
26.0.4米
【分析】由“长方体的体积=长×宽×高”可知,高=长方体的体积÷长÷宽,把题中数据代入公式求出这些沙子可以铺的厚度,据此解答。
【详解】38分米=3.8米
7.6÷5÷3.8
=1.52÷3.8
=0.4(米)
答:可以铺0.4米厚。
【点睛】本题主要考查长方体体积公式的应用,灵活运用公式是解答题目的关键。
27.3000cm3
【分析】截成2段后,表面积比原来增加了2个横截面的面积,因为表面积是增加了60平方厘米,由此即可求出横截面的面积是60÷2=30平方厘米,由此再乘以长就是这根木料的体积。
【详解】1米=100厘米
60÷2×100
=30×100
=3000(立方厘米)
答:这根木料的体积是3000立方厘米。
【点睛】抓住长方体的切割特点和增加的表面积求出长方体的横截面的面积是解决此题的关键。
28.126千克
【分析】根据长方体的体积=底面积×高,求出汽油桶的容积,乘每升汽油的重量即可。
【详解】30×6×0.7
=180×0.7
=126(千克)
答:这个油桶可以装126千克汽油。
【点睛】此题主要考查了长方体容积的相关应用,先求出汽油桶的容积是解题关键。
29.7.02吨
【分析】根据“长方体体积=长×宽×高”求出长方体钢材的体积,再乘每立方分米钢材的质量即可。
【详解】30×6×5×7.8
=900×7.8
=7020(千克)
7020千克=7.02吨
答:这块钢材的质量是7.02吨。
【点睛】熟练掌握长方体的体积计算公式是解答本题的关键。
30.360000毫升;360升
【分析】容积为物体所能容纳物体的体积,统一单位,将1.2米转化为120厘米。 水槽的容积=长方体的体积=长×宽×高,据此代入数据求出容积。
【详解】1.2米=120厘米
120×60×50
=7200×50
=360000(立方厘米)
360000立方厘米=360000毫升=360升
答:这个水槽容积是360000毫升。合360升。
【点睛】此题考查了长方体容积的计算,注意升与毫升进率是1000。
答案第2页,共9页
答案第3页,共9页
