2015连线中考数学一轮复习系列专题14图形认识初步
文档属性
| 名称 | 2015连线中考数学一轮复习系列专题14图形认识初步 |  | |
| 格式 | zip | ||
| 文件大小 | 716.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 17:44:27 | ||
图片预览



文档简介
基础知识
知识点一:图形的分类
图形的分类
立体图形三视图:
①、三视图的定义:从正面得到的视图叫做主视图,从上面得到的视图叫做俯视图,从左面得到的视图叫做左视图。
②、画三视图必须遵循的法则:
、同一物体的主视图和左视图的高相同
、同一物体的主视图和俯视图的长相同
、同一物体的左视图和俯视图的宽相同
③、基本几何体的三视图
图形 主视图 左视图 俯视图
正方体 正方形 正方形 正方形
长方体 长方形 长方形 长方形
圆柱 长方形 长方形 圆
圆锥 三角形 三角形 圆(存在圆心)
正四棱锥 三角形 三角形 正方形
球体 圆 圆 圆
3、常见的立体图形的平面展开图.
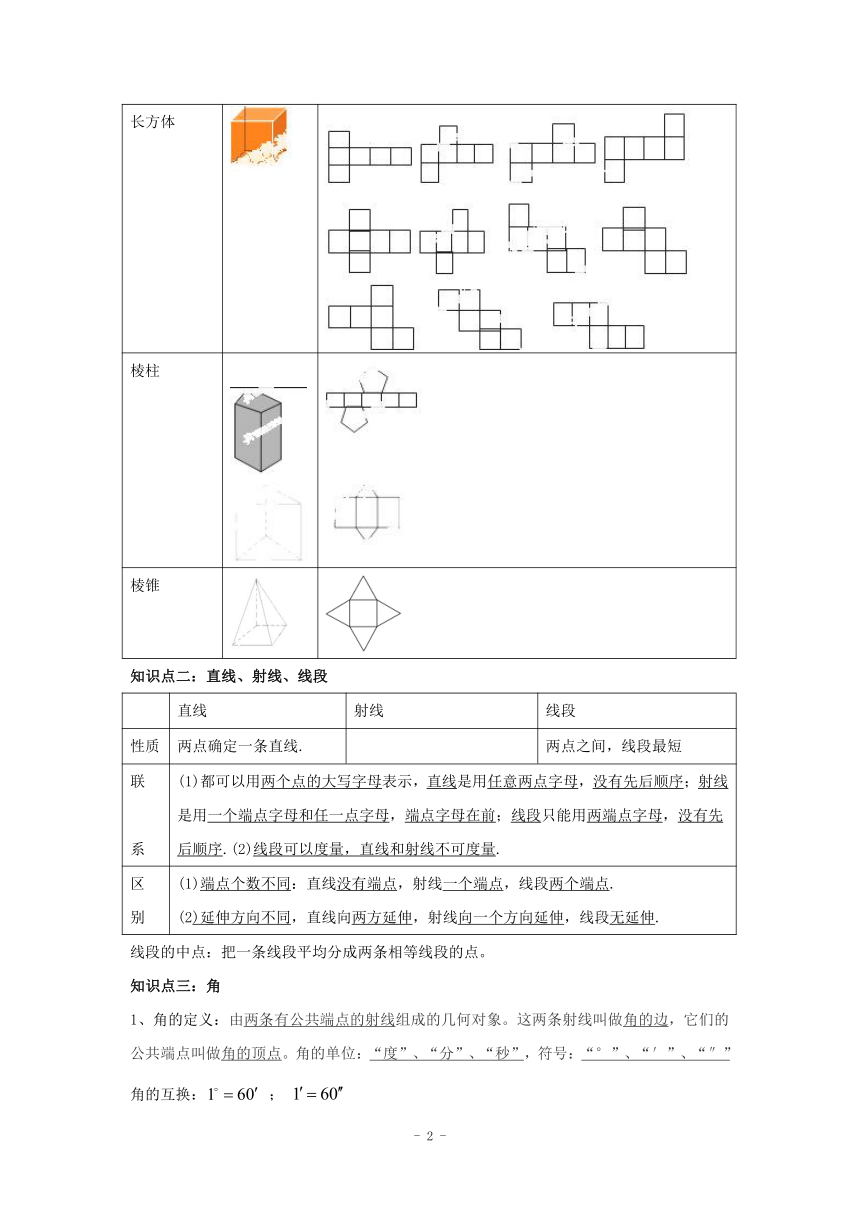
常见的立体图形名称 立体图形 平面展开图
圆柱
圆锥
长方体
棱柱
棱锥
知识点二:直线、射线、线段
直线 射线 线段
性质 两点确定一条直线. 两点之间,线段最短
联系 (1)都可以用两个点的大写字母表示,直线是用任意两点字母,没有先后顺序;射线是用一个端点字母和任一点字母,端点字母在前;线段只能用两端点字母,没有先后顺序.(2)线段可以度量,直线和射线不可度量.
区别 (1)端点个数不同:直线没有端点,射线一个端点,线段两个端点.(2)延伸方向不同,直线向两方延伸,射线向一个方向延伸,线段无延伸.
线段的中点:把一条线段平均分成两条相等线段的点。
知识点三:角
1、角的定义:由两条有公共端点的射线组成的几何对象。这两条射线叫做角的边,它们的公共端点叫做角的顶点。角的单位:“度”、“分”、“秒”,符号:“°”、“′”、“″”角的互换: ;
2、比较角大小的方法:度量法、叠合法.
度量法:利用量角器将每个角都量出度数。
叠合法:用圆规将其他的角画一个角上(公共端点和一条边)再根据另一条边的位置判断出其大小。
3、互余、互补
、互余:两角之和为90°就称这两个角“互为余角”,简称“互余”。
、互补:两角之和为180°就称这两个角“互为补角”,简称“互补”。
补角的性质:①、同角的补角相等;②、等角的补角相等。
知识点四:相交线
相交线的定义:在同一平面内,相交的两条直线。(特点:有一个交点)
两条直线相交产生的角
①、对顶角:如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点, 那么这两个角是对顶角
特点:、有一个公共顶点 、两边互为反向延长线
性质:对顶角相等
条直线相交有对对顶角
②、邻补角:两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,叫做邻补角。
性质:邻补角互补(和为180°)
条直线相交有对邻补角
垂线:同一平面内,两条直线相交,所成的夹角均为90°时,称这两条直线互相垂直。
性质:、过直线外一点有且只有一条直线与已知直线垂直
、垂线段最短
点到直线的距离:点到直线的垂线段的长度。
知识点五:平行线
1、平行线:在同一平面内,不相交的两条直线。(特点:没有交点)
2、平行公理:过直线外一点有且只有一条直线与已知直线平行
推论:如果有一条直线与其它两条直线平行,那么另外两条直线也平行。
三线八角
形成方式:两条直线被第三条直线所截(这两条直线不一定平行)
同位角:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一方,我们把这种位置关系的角称为同位角。如图16-1中的∠3和∠6;∠5和∠4;∠1和∠8,;∠2和∠7.
内错角:直线a,b被第三条直线c所截(或说a,b相交c),分别在截线的两侧,且夹在两条被截直线a,b之间,具有这样位置关系的一对角叫做内错角。如图16-1中的∠1和∠6,;∠2和∠5.
同旁内角:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线同旁,且在被截线之内的两角,叫做同旁内角。如图16-1中的∠1和∠5,;∠2和∠6.
平行线的判定方法
①、同位角相等,两直线平行;
②、内错角相等,两直线平行;
③、同旁内角互补,;两直线平行。
平行线的性质
①、两直线平行,同位角相等;
②、两直线平行,内错角相等;
③、两直线平行,同旁内角互补;
两平行线间的距离:就是两条平行线间的垂线段的长度。
知识点六:命题
定义:可以判断一件事情对错的陈述句,叫做命题
分类:
①、真命题:正确的命题
②、假命题:错误的命题
组成:(1)题设(如果……) (2)结论(那么……)
知识点六:平移
定义:一个图形沿着一定的方向平行移动
特点:
①、平移后图形的形状、大小不变,位置改变
②、对应点所连接的线段互相平行(或在同一直线上),对应角相等。
重点例题分析
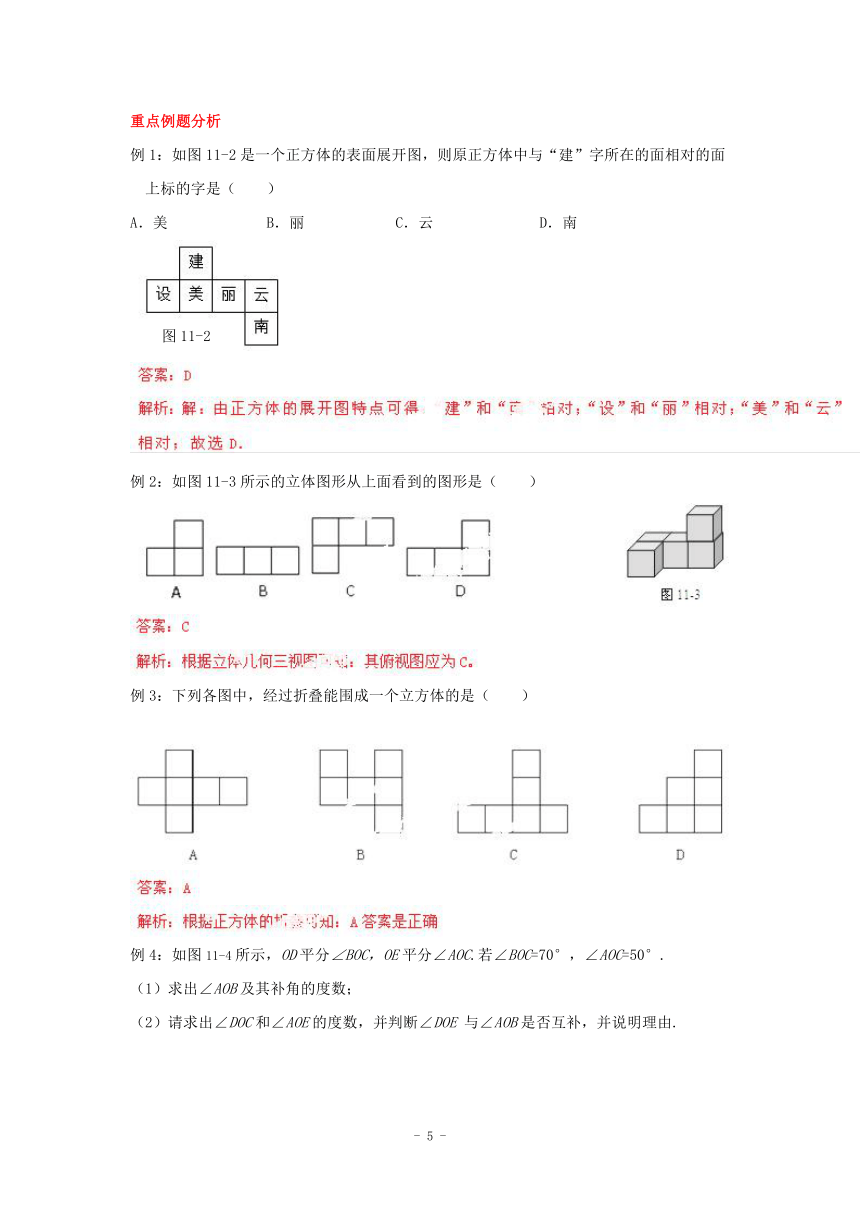
例1:如图11-2是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
A.美 B.丽 C.云 D.南
例2:如图11-3所示的立体图形从上面看到的图形是( )
例3:下列各图中,经过折叠能围成一个立方体的是( )
例4:如图11-4所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE 与∠AOB是否互补,并说明理由.
例5:关于直线、射线、线段的有关说法正确的有( )
(1)直线AB和直线BA是同一条直线
(2)射线AB和射线BA是同一条射线
(3)线段AB和线段BA是同一条线段
(4)线段一定比直线短
(5)射线一定比直线短
(6)线段的长度能够度量,而直线、射线的长度不可能度量.
A.2 B.3 C.4 D.5
综上可得(1)(3)(6)正确.
故选B.
例6:下列命题中是假命题的是( )
过已知直线上一点及该直线外一点的直线与已知直线必是相交线
直角的补角是直角
同旁内角互补
D. 从直线外一点向直线作线段,垂线段最短
例7:如图11-5,直线l1∥l2,则∠α为( )
A.150° B.140° C.130° D.120°
例8:如图11-6,在灯塔A处看海岛B在南偏西50°方向,看海岛C在南偏东20°方向,在C处看海岛B在南偏西80°方向,求∠ACB的度数.
例9:根据下列要求画图.
(1)如图(1)所示,过点A画MN∥BC;
(2)如图 (2)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;
(3)如图(3)所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交 于点F.
(1) (2) (3)
巩固练习
1、下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从地到地架设电线,总是尽可能沿着线段架设;④把弯曲的公路改直,就能缩短路程.其中可用“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②④ D.③④
2、在直线上顺次取A、B、C三点,使得AB=5㎝,BC=3㎝,如果O是线段AC的中点,那么线段OB的长度是( )
A.2㎝ B.1㎝ C.1.5㎝ D.0.5㎝
3、如图11-7所示,从A地到达B地,最短的路线是( )
A.A→C→E→B B.A→F→E→B
C.A→D→E→B D.A→C→G→E→B
如图11-8,AB⊥CD于点B,BE是∠ABD的平分线,则∠CBE= 度.
5、下列语句错误的是( )
A.连接两点的线段的长度叫做两点间的距离; B.两条直线平行,同旁内角互补
C.若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角
D.平移变换中,各组对应点连成两线段平行且相等
6、如图11-19,,分别在上,为两平行线间一点,那么( )
A. B. C. D.
7、(2014年广东汕尾,第6题4分)如图11-10,能判定EB∥AC的条件是( )
A.∠C=∠ABE B. ∠A=∠EBD C. ∠C=∠ABC D. ∠A=∠ABE
8、用同样大小的黑色棋子按如图11-9所示的规律摆放:
(1)第5个图形有多少颗黑色棋子?
(2)第几个图形有2 013颗黑色棋子?请说明理由.
9、( 2014 广东,第19题6分)如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
中考预测
1、一个立体图形的三视图如图11-12所示,那么它是 ( )
A.圆锥 B.球
C.三棱锥 D.四棱锥
2、(2014 四川巴中,第3题3分)如图11-13,CF是△ABC的外角∠ACM的平分线,且CF∥AB,
∠ACF=50°,则∠B的度数为( )
A.80° B. 40° C.60° D. 50°
3、如图11-14,已知则______.
4、(2014 湖南怀化,第2题,3分)将一直角三角板与两边平行的纸条如图11-15放置.已知∠1=30°,则∠2的度数为( )
A.30° B.45° C.50° D.60°
参考答案
巩固练习
6、C
7、D
图16-1
图11-2
图11-6
图11-15
PAGE
- 15 -
知识点一:图形的分类
图形的分类
立体图形三视图:
①、三视图的定义:从正面得到的视图叫做主视图,从上面得到的视图叫做俯视图,从左面得到的视图叫做左视图。
②、画三视图必须遵循的法则:
、同一物体的主视图和左视图的高相同
、同一物体的主视图和俯视图的长相同
、同一物体的左视图和俯视图的宽相同
③、基本几何体的三视图
图形 主视图 左视图 俯视图
正方体 正方形 正方形 正方形
长方体 长方形 长方形 长方形
圆柱 长方形 长方形 圆
圆锥 三角形 三角形 圆(存在圆心)
正四棱锥 三角形 三角形 正方形
球体 圆 圆 圆
3、常见的立体图形的平面展开图.
常见的立体图形名称 立体图形 平面展开图
圆柱
圆锥
长方体
棱柱
棱锥
知识点二:直线、射线、线段
直线 射线 线段
性质 两点确定一条直线. 两点之间,线段最短
联系 (1)都可以用两个点的大写字母表示,直线是用任意两点字母,没有先后顺序;射线是用一个端点字母和任一点字母,端点字母在前;线段只能用两端点字母,没有先后顺序.(2)线段可以度量,直线和射线不可度量.
区别 (1)端点个数不同:直线没有端点,射线一个端点,线段两个端点.(2)延伸方向不同,直线向两方延伸,射线向一个方向延伸,线段无延伸.
线段的中点:把一条线段平均分成两条相等线段的点。
知识点三:角
1、角的定义:由两条有公共端点的射线组成的几何对象。这两条射线叫做角的边,它们的公共端点叫做角的顶点。角的单位:“度”、“分”、“秒”,符号:“°”、“′”、“″”角的互换: ;
2、比较角大小的方法:度量法、叠合法.
度量法:利用量角器将每个角都量出度数。
叠合法:用圆规将其他的角画一个角上(公共端点和一条边)再根据另一条边的位置判断出其大小。
3、互余、互补
、互余:两角之和为90°就称这两个角“互为余角”,简称“互余”。
、互补:两角之和为180°就称这两个角“互为补角”,简称“互补”。
补角的性质:①、同角的补角相等;②、等角的补角相等。
知识点四:相交线
相交线的定义:在同一平面内,相交的两条直线。(特点:有一个交点)
两条直线相交产生的角
①、对顶角:如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点, 那么这两个角是对顶角
特点:、有一个公共顶点 、两边互为反向延长线
性质:对顶角相等
条直线相交有对对顶角
②、邻补角:两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,叫做邻补角。
性质:邻补角互补(和为180°)
条直线相交有对邻补角
垂线:同一平面内,两条直线相交,所成的夹角均为90°时,称这两条直线互相垂直。
性质:、过直线外一点有且只有一条直线与已知直线垂直
、垂线段最短
点到直线的距离:点到直线的垂线段的长度。
知识点五:平行线
1、平行线:在同一平面内,不相交的两条直线。(特点:没有交点)
2、平行公理:过直线外一点有且只有一条直线与已知直线平行
推论:如果有一条直线与其它两条直线平行,那么另外两条直线也平行。
三线八角
形成方式:两条直线被第三条直线所截(这两条直线不一定平行)
同位角:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一方,我们把这种位置关系的角称为同位角。如图16-1中的∠3和∠6;∠5和∠4;∠1和∠8,;∠2和∠7.
内错角:直线a,b被第三条直线c所截(或说a,b相交c),分别在截线的两侧,且夹在两条被截直线a,b之间,具有这样位置关系的一对角叫做内错角。如图16-1中的∠1和∠6,;∠2和∠5.
同旁内角:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线同旁,且在被截线之内的两角,叫做同旁内角。如图16-1中的∠1和∠5,;∠2和∠6.
平行线的判定方法
①、同位角相等,两直线平行;
②、内错角相等,两直线平行;
③、同旁内角互补,;两直线平行。
平行线的性质
①、两直线平行,同位角相等;
②、两直线平行,内错角相等;
③、两直线平行,同旁内角互补;
两平行线间的距离:就是两条平行线间的垂线段的长度。
知识点六:命题
定义:可以判断一件事情对错的陈述句,叫做命题
分类:
①、真命题:正确的命题
②、假命题:错误的命题
组成:(1)题设(如果……) (2)结论(那么……)
知识点六:平移
定义:一个图形沿着一定的方向平行移动
特点:
①、平移后图形的形状、大小不变,位置改变
②、对应点所连接的线段互相平行(或在同一直线上),对应角相等。
重点例题分析
例1:如图11-2是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
A.美 B.丽 C.云 D.南
例2:如图11-3所示的立体图形从上面看到的图形是( )
例3:下列各图中,经过折叠能围成一个立方体的是( )
例4:如图11-4所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE 与∠AOB是否互补,并说明理由.
例5:关于直线、射线、线段的有关说法正确的有( )
(1)直线AB和直线BA是同一条直线
(2)射线AB和射线BA是同一条射线
(3)线段AB和线段BA是同一条线段
(4)线段一定比直线短
(5)射线一定比直线短
(6)线段的长度能够度量,而直线、射线的长度不可能度量.
A.2 B.3 C.4 D.5
综上可得(1)(3)(6)正确.
故选B.
例6:下列命题中是假命题的是( )
过已知直线上一点及该直线外一点的直线与已知直线必是相交线
直角的补角是直角
同旁内角互补
D. 从直线外一点向直线作线段,垂线段最短
例7:如图11-5,直线l1∥l2,则∠α为( )
A.150° B.140° C.130° D.120°
例8:如图11-6,在灯塔A处看海岛B在南偏西50°方向,看海岛C在南偏东20°方向,在C处看海岛B在南偏西80°方向,求∠ACB的度数.
例9:根据下列要求画图.
(1)如图(1)所示,过点A画MN∥BC;
(2)如图 (2)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;
(3)如图(3)所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交 于点F.
(1) (2) (3)
巩固练习
1、下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从地到地架设电线,总是尽可能沿着线段架设;④把弯曲的公路改直,就能缩短路程.其中可用“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②④ D.③④
2、在直线上顺次取A、B、C三点,使得AB=5㎝,BC=3㎝,如果O是线段AC的中点,那么线段OB的长度是( )
A.2㎝ B.1㎝ C.1.5㎝ D.0.5㎝
3、如图11-7所示,从A地到达B地,最短的路线是( )
A.A→C→E→B B.A→F→E→B
C.A→D→E→B D.A→C→G→E→B
如图11-8,AB⊥CD于点B,BE是∠ABD的平分线,则∠CBE= 度.
5、下列语句错误的是( )
A.连接两点的线段的长度叫做两点间的距离; B.两条直线平行,同旁内角互补
C.若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角
D.平移变换中,各组对应点连成两线段平行且相等
6、如图11-19,,分别在上,为两平行线间一点,那么( )
A. B. C. D.
7、(2014年广东汕尾,第6题4分)如图11-10,能判定EB∥AC的条件是( )
A.∠C=∠ABE B. ∠A=∠EBD C. ∠C=∠ABC D. ∠A=∠ABE
8、用同样大小的黑色棋子按如图11-9所示的规律摆放:
(1)第5个图形有多少颗黑色棋子?
(2)第几个图形有2 013颗黑色棋子?请说明理由.
9、( 2014 广东,第19题6分)如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
中考预测
1、一个立体图形的三视图如图11-12所示,那么它是 ( )
A.圆锥 B.球
C.三棱锥 D.四棱锥
2、(2014 四川巴中,第3题3分)如图11-13,CF是△ABC的外角∠ACM的平分线,且CF∥AB,
∠ACF=50°,则∠B的度数为( )
A.80° B. 40° C.60° D. 50°
3、如图11-14,已知则______.
4、(2014 湖南怀化,第2题,3分)将一直角三角板与两边平行的纸条如图11-15放置.已知∠1=30°,则∠2的度数为( )
A.30° B.45° C.50° D.60°
参考答案
巩固练习
6、C
7、D
图16-1
图11-2
图11-6
图11-15
PAGE
- 15 -
同课章节目录
