2015连线中考数学一轮复习系列专题10反比例函数
文档属性
| 名称 | 2015连线中考数学一轮复习系列专题10反比例函数 |  | |
| 格式 | zip | ||
| 文件大小 | 905.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 17:44:47 | ||
图片预览




文档简介
第十讲 反比例函数
基础知识
知识点一:反比例函数的有关概念
定义:一般地,形如(为常数,)的函数称为反比例函数。还可以写成。
知识点二:反比例函数的基本性质
反比例函数的图像:
反比例函数的图像是双曲线,是轴对称图形(对称轴是或);(为常数,)中自变量,函数值,所以双曲线是不经过原点,断开的两个分支,延伸部分逐渐靠近坐标轴,但是永远不与坐标轴相交;
作图方法:描点法
列表(应以O为中心,沿O的两边分别取三对或以上互为相反的数)
描点(有小到大的顺序)
连线(从左到右光滑的曲线)
反比例函数的几何意义:
反比例函数()中比例系数的几何意义是:过双曲线 ()上任意引轴轴的垂线,所得矩形面积为。
反比例函数的基本性质
反比例函数
的取值
图像
性质 ①、的取值范围是;的取值范围是②、函数图像分别在第一、三象限,在每个象限内,随着的增大而减小③、对称轴为直线④、若点在反比例函数图像上,则点也一定在此反比例函数图像上。 ①、的取值范围是;的取值范围是②、函数图像分别在第二、四象限,在每个象限内,随着的增大而增大③、对称轴为直线④、若点在反比例函数图像上,则点也一定在此反比例函数图像上。
5、反比例函数解析式的确定:利用待定系数法(只需一对对应值或图像上一个点的坐标即可求出)
重点例题分析
例1:如果函数的图像是双曲线,且在第二,四象限内,那么该函数的解析式是多少?
例2:在反比例函数的图像上有三点,,,,, 。若则下列各式正确的是( )
A. B. C. D.
例3:如果一次函数相交于点(),那么该直线与双曲线的另一个交点为 。
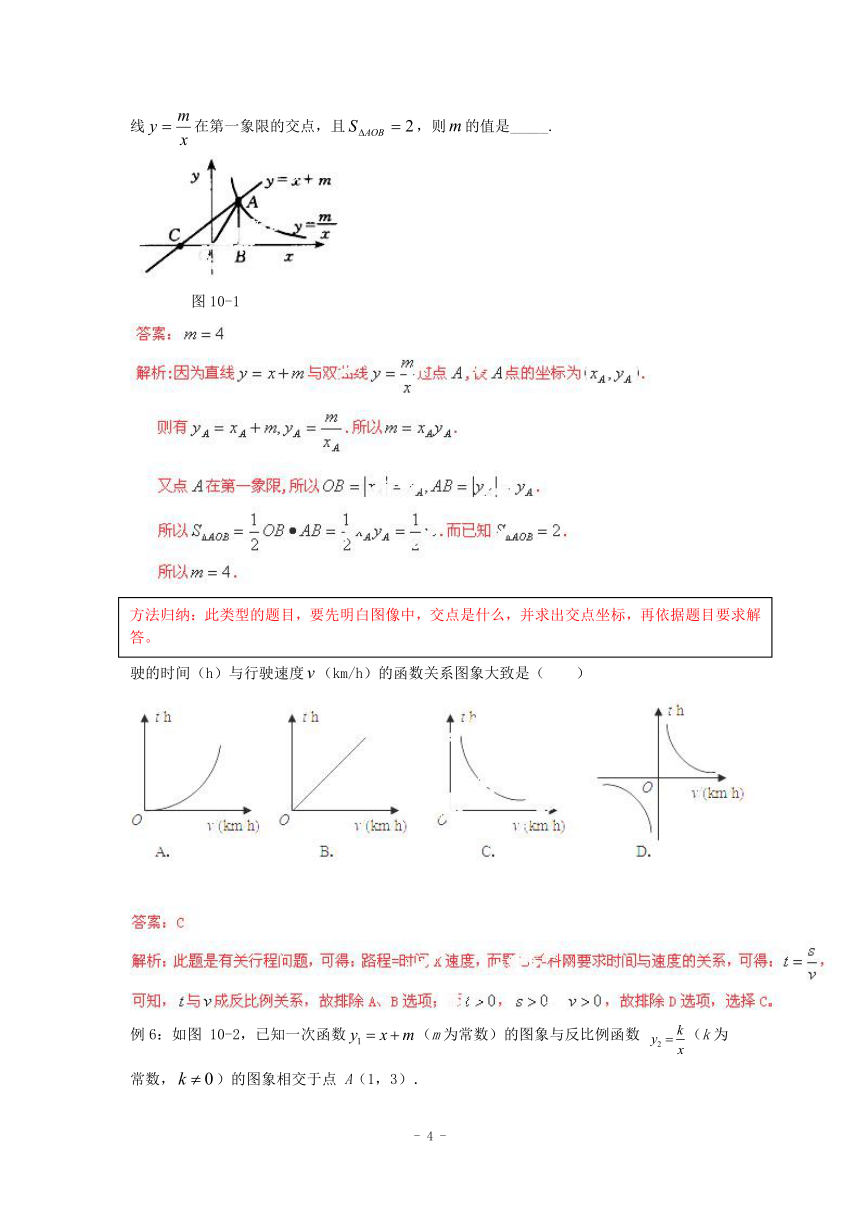
例4:如图10-1,在中,点是直线与双曲线在第一象限的交点,且,则的值是_____.
图10-1
例5:(2007南宁)已知甲、乙两地相距(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间(h)与行驶速度(km/h)的函数关系图象大致是( )
例6:如图 10-2,已知一次函数(m为常数)的图象与反比例函数 (k为常数,)的图象相交于点 A(1,3).
(1)求这两个函数的解析式及其图象的另一交点的坐标;
(2)观察图象,写出使函数值的自变量的取值范围.
例7:(2014 武汉,第15题3分)如图10-3,若双曲线与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且OC=3BD,则实数k的值为 .
故k=×12=.故答案为:.
例8:(2014年云南省,第17题6分)将油箱注满k升油后,轿车科行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
巩固练习
1、若双曲线y=的图象经过第二、四象限,则k的取值范围是( )
A.k>0 B.k<0 C.k≠0 D.不存在
2、关于反比例函数y=的图象,下列说法正确的是( )
A.必经过点(1,1) B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称 D.两个分支关于原点成中心对称
函数y=2x与函数y=在同一坐标系中的大致图象是( )
4、反比例函数y=(m-2)x2m+1的函数值为时,自变量x的值是____________
5、(2014 济宁,第14题3分)如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
6、(2014年四川资阳,第20题8分)如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
7、( 2014 珠海,第19题7分)如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边在AD在x轴上,点B在第四象限,直线BD与反比例函数的图象交于点B、E.
(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标.
8、(2014 舟山,第22题10分)实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
9、(2014 浙江宁波,第22题10分)如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=,反比例函数y=(k>0)的图象过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,是判断点G是否在反比例函数的图象上,并说明理由.
中考预测
1、已知一次函数y1=kx+b(ky2时,实数x的取值范围是( )
A.x<-l或O3 D.O2、已知抛物线y=x2﹣2x+m+1与x轴有两个不同的交点,则函数的大致图象是( )
3、函数y=mx+n与,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )
A B C D
4、在反比例函数y=图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是______________.
5、已知反比例函数y=(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而增大,那么这个反比例函数的解析式是: (只需写一个).
6、如图,在平面直角坐标系中,已知一次函数的图像经过点,与反比例函数的图像相交于点
①求m的值和一次函数的解析式;
②结合图象直接写出:当x>0时,不等式的解集.
7、如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣>0的解集.
8、如图①,△OAB中,A(0,2),B(4,0),将△AOB向右平移m个单位,得到△O′A′B′.
(1)当m=4时,如图②.若反比例函数y=的图象经过点A′,一次函数y=ax+b的图象经过A′、B′两点.求反比例函数及一次函数的表达式;
(2)若反比例函数y=的图象经过点A′及A′B′的中点M,求m的值.
2.D
B
4、-9
5、2
2、A
3、B
4、
解:由题可知:反比例函数y=图象的每一支曲线上,y都随x的增大而减小
故:,即
5.(答案不唯一)
注意点:
1、
2、等号右边是一个分式,分母中含有自变量,且指数为1
3、自变量的取值为一切非零实数;函数的取值是一切非零实数
方法归纳:此类型的题目,要先明白图像中,交点是什么,并求出交点坐标,再依据题目要求解答。
PAGE
- 2 -
基础知识
知识点一:反比例函数的有关概念
定义:一般地,形如(为常数,)的函数称为反比例函数。还可以写成。
知识点二:反比例函数的基本性质
反比例函数的图像:
反比例函数的图像是双曲线,是轴对称图形(对称轴是或);(为常数,)中自变量,函数值,所以双曲线是不经过原点,断开的两个分支,延伸部分逐渐靠近坐标轴,但是永远不与坐标轴相交;
作图方法:描点法
列表(应以O为中心,沿O的两边分别取三对或以上互为相反的数)
描点(有小到大的顺序)
连线(从左到右光滑的曲线)
反比例函数的几何意义:
反比例函数()中比例系数的几何意义是:过双曲线 ()上任意引轴轴的垂线,所得矩形面积为。
反比例函数的基本性质
反比例函数
的取值
图像
性质 ①、的取值范围是;的取值范围是②、函数图像分别在第一、三象限,在每个象限内,随着的增大而减小③、对称轴为直线④、若点在反比例函数图像上,则点也一定在此反比例函数图像上。 ①、的取值范围是;的取值范围是②、函数图像分别在第二、四象限,在每个象限内,随着的增大而增大③、对称轴为直线④、若点在反比例函数图像上,则点也一定在此反比例函数图像上。
5、反比例函数解析式的确定:利用待定系数法(只需一对对应值或图像上一个点的坐标即可求出)
重点例题分析
例1:如果函数的图像是双曲线,且在第二,四象限内,那么该函数的解析式是多少?
例2:在反比例函数的图像上有三点,,,,, 。若则下列各式正确的是( )
A. B. C. D.
例3:如果一次函数相交于点(),那么该直线与双曲线的另一个交点为 。
例4:如图10-1,在中,点是直线与双曲线在第一象限的交点,且,则的值是_____.
图10-1
例5:(2007南宁)已知甲、乙两地相距(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间(h)与行驶速度(km/h)的函数关系图象大致是( )
例6:如图 10-2,已知一次函数(m为常数)的图象与反比例函数 (k为常数,)的图象相交于点 A(1,3).
(1)求这两个函数的解析式及其图象的另一交点的坐标;
(2)观察图象,写出使函数值的自变量的取值范围.
例7:(2014 武汉,第15题3分)如图10-3,若双曲线与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且OC=3BD,则实数k的值为 .
故k=×12=.故答案为:.
例8:(2014年云南省,第17题6分)将油箱注满k升油后,轿车科行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
巩固练习
1、若双曲线y=的图象经过第二、四象限,则k的取值范围是( )
A.k>0 B.k<0 C.k≠0 D.不存在
2、关于反比例函数y=的图象,下列说法正确的是( )
A.必经过点(1,1) B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称 D.两个分支关于原点成中心对称
函数y=2x与函数y=在同一坐标系中的大致图象是( )
4、反比例函数y=(m-2)x2m+1的函数值为时,自变量x的值是____________
5、(2014 济宁,第14题3分)如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
6、(2014年四川资阳,第20题8分)如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
7、( 2014 珠海,第19题7分)如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边在AD在x轴上,点B在第四象限,直线BD与反比例函数的图象交于点B、E.
(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标.
8、(2014 舟山,第22题10分)实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
9、(2014 浙江宁波,第22题10分)如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=,反比例函数y=(k>0)的图象过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,是判断点G是否在反比例函数的图象上,并说明理由.
中考预测
1、已知一次函数y1=kx+b(k
A.x<-l或O
3、函数y=mx+n与,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )
A B C D
4、在反比例函数y=图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是______________.
5、已知反比例函数y=(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而增大,那么这个反比例函数的解析式是: (只需写一个).
6、如图,在平面直角坐标系中,已知一次函数的图像经过点,与反比例函数的图像相交于点
①求m的值和一次函数的解析式;
②结合图象直接写出:当x>0时,不等式的解集.
7、如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣>0的解集.
8、如图①,△OAB中,A(0,2),B(4,0),将△AOB向右平移m个单位,得到△O′A′B′.
(1)当m=4时,如图②.若反比例函数y=的图象经过点A′,一次函数y=ax+b的图象经过A′、B′两点.求反比例函数及一次函数的表达式;
(2)若反比例函数y=的图象经过点A′及A′B′的中点M,求m的值.
2.D
B
4、-9
5、2
2、A
3、B
4、
解:由题可知:反比例函数y=图象的每一支曲线上,y都随x的增大而减小
故:,即
5.(答案不唯一)
注意点:
1、
2、等号右边是一个分式,分母中含有自变量,且指数为1
3、自变量的取值为一切非零实数;函数的取值是一切非零实数
方法归纳:此类型的题目,要先明白图像中,交点是什么,并求出交点坐标,再依据题目要求解答。
PAGE
- 2 -
同课章节目录
