2015连线中考数学一轮复习系列专题4方程和二元一次方程组
文档属性
| 名称 | 2015连线中考数学一轮复习系列专题4方程和二元一次方程组 |

|
|
| 格式 | zip | ||
| 文件大小 | 466.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 00:00:00 | ||
图片预览




文档简介
基础知识
知识点一、 等式的性质
等式性质1.等式两边都加上或减去同一个数或一个整式,所得的结果仍是等式.
用字母表示: 若a=b,那么.
等式性质2. 等式两边同乘以或除以同一个不等于零的数,所得的结果仍是等式.
用字母表示: 若a=b,那么am=bm,
知识点二、方程、方程的解的概念
1. 方程
含有未知数的等式叫方程.方程中只含有一个未知数,并且未知数的指数是l,这样的方程叫一元一次方程,其一般形式为ax +b = 0 (a、b为常数,且a≠0);方程中含有两个未知数(x和y),并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程,一般形式:ax+by+c=o(a≠0, b≠0).
2.方程的解
能够使方程左右两边相等的未知数的值是方程的解.一般地,一元一次方程有唯一解,二元一次方程有无数组解,二元一次方程组有唯一解.
知识点三、 一元一次方程、二元一次方程的解法、步骤
1. 解一元一次方程的步骤
变形名称 具体做法 注意事项
去分母 在方程的两边同乘以各分母的最小公倍数 (1)不要漏乘不含分母的项(2)分子是一个整体,去分母后应加括号
去括号 先去小括号,再去中括号,最后去大括号(或由外向内) (1)不要漏乘括号里的项(2)注意“+”“-”号的改变
移项 把含有未知数的项都移到方程的另一边 (1)移项要变号(2)不要漏掉项
合并同类项 把方程化为ax=b(a≠0)的形式 字母及其指数不变,系数相加
系数化为1 在方程两边都乘以未知数的系数a,的得到方程的解 不要把分子、分母位置颠倒
2. 二元一次方程组的解法
解二元一次方程组的基本思想是“消元”,将“二元”转化为“一元”。通常的方法有:代入消元法和加减消元法.
代人消元法:把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代人另一个方程,实现消元,进而求得这个二元一次方程组的解,简称代人法.
加减消元法:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,简称加减法.
其实二元一次方程组的解法还有图像法,两个一次函数的交点坐标就是两个解析式联立方程组的解.
知识点四、列方程解应用题的一般步骤
列方程解决实际问题通常有下列几个步骤:
①审:审题,分析题中已知什么,求什么,明确各数量之间的关系
②设:设未知数,用字母表示适当是未知数.
③找:找出能够表示应用题全部意义的一个相等关系.
④列:根据题中的相等关系列出方程.
⑤解:解方程,求出未知数的值
⑥答:检验所得解是否符合题意,写出问题的答案.
重点例题解析
例1. (滨州)把方程变形为x=2,其依据是( )
A.等式的性质1 B.等式的性质2
C.分式的基本性质 D.不等式的性质1
例2. (孝感)已知是二元一次方程组的解,则的值是( )
A. B. C. D.
例3.(毕节)若与可以合并成一项,则的值是( )
A.2 B.0 C.-1 D.1
例4. (达州)如图,已知函数y=ax+b和y=cx+d的图象交于点M,则根据图象可知,关于x,y的二元一次方程组 的解为 .
例5. 解下列方程(组)
(1) (2)
例6. (福州)把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本则还缺25本.这个班有多少学生?
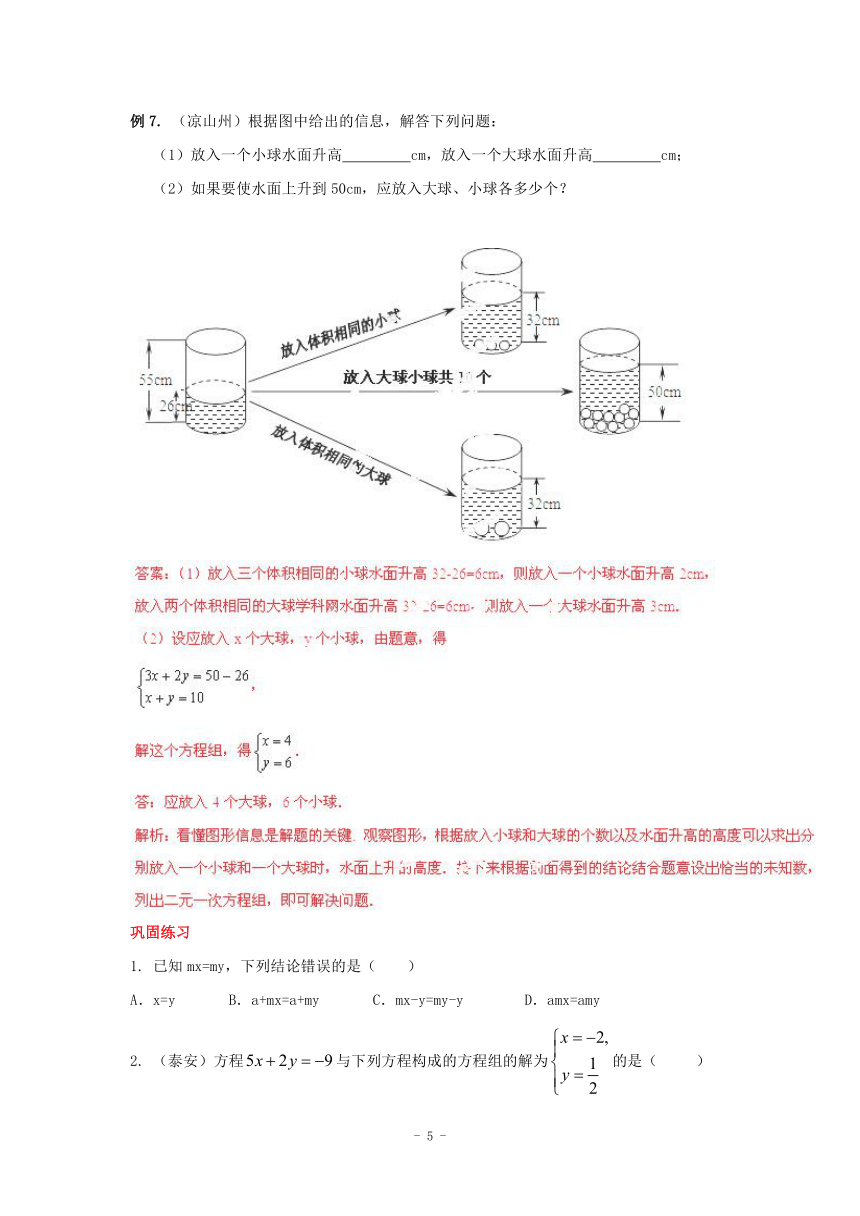
例7. (凉山州)根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 cm,放入一个大球水面升高 cm;
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
巩固练习
1. 已知mx=my,下列结论错误的是( )
A.x=y B.a+mx=a+my C.mx-y=my-y D.amx=amy
2. (泰安)方程与下列方程构成的方程组的解为的是( )
A. B. C. D.
3. (莆田)若x、y满足方程组,则x —y的值等于( )
A.—1 B.1 C.2 D.3
4. (恩施)“六一”期间,某商店将单价标为130元的书包按8折出售可获得30%,该书包每个的进价是( )
A.65元 B.80元 C.100元 D. 104元
5. (娄底)已知关于x的方程2x+a-5=0的解是x=2,则a的值为____________.
6. (徐州)函数y=2x与y=x+1的图象的交点坐标为 .
7. (宁夏)若2a-b=5,a-2b=4,则a-b的值为______.
8. 解下列方程(组)
(1)解方程: (2) 解方程组 eq \b\lc\{()
9. (齐齐哈尔)将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有 ( )
A.6种 B.7种 C.8种 D.9种
10. 如图,用10块相同的长方形纸板拼成一个矩形,设长方形纸板的长和宽分别为xcm和ycm,则依题意列方程式组正确的是( )
A B C D
11. (宁波)用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和 2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用 A方法,其余用 B方法.
(1)用 x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若栽剪出的侧面和底面恰好全部用完,问能做多少个盒子?
12.(南昌)小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.
妈妈:“今天买这两样菜共花了45元,上月买同重量的这两种菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨了50%,排骨的单价上涨了20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).
中考预测
1. 方程组 的解为( )
A. B. C. D.
2. 已知是方程组的解,则a-b的值是( )
A.-1 B.2 C.3 D.4
3. 若,则实数a在数轴上的对应点一定在( )
A.原点左侧 B.原点或原点左侧 C.原点右侧 D.原点或原点右侧
4. 已知,则x+y的值为( )
A.0 B.-1 C.1 D.5
5. 由方程组可得出x与y的关系是( )
A. B. C. D.
6.已知x、y是二元一次方程组的解,则代数式x2-4y2的值为 .
7. 如图,已知函数y=2x+b与函数y=kx-3的图象交于点P,则方程组 的解是 .
8.哥哥与弟弟的年龄和是18岁,弟弟对哥哥说:“当我的年龄是你现在年龄的时候,你就是
18岁,”如果现在弟弟的年龄是x岁,哥哥的年龄是y岁,根据题意列出方程组
是 .
9.今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3
分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数
是所负场数的整数倍,则小虎足球队所负场数的情况有( )
A. 2种 B. 3种 C. 4种 D. 5 种
10.情境:
试根据图中的信息,解答下列问题:
购买6根跳绳需 元,购买12根跳绳需 元;
小红比小明多买2根,付款时小红反而比小明少5元.你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
11.如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”.现向容器内匀速注水,注满为止.在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为____________cm,匀速注水的水流速度为__________cm/s;
(2)若“几何体”的下方圆柱的底面积为15cm,求“几何体”上方圆柱的高和底面积.
12.几个小伙伴打算去音乐厅观看演出,他们准备用360元钱购买门票.下面是两个小伙伴的对话:
根据对话中的信息,请你求出小伙伴们的人数.
中考预测
PAGE
- 13 -
知识点一、 等式的性质
等式性质1.等式两边都加上或减去同一个数或一个整式,所得的结果仍是等式.
用字母表示: 若a=b,那么.
等式性质2. 等式两边同乘以或除以同一个不等于零的数,所得的结果仍是等式.
用字母表示: 若a=b,那么am=bm,
知识点二、方程、方程的解的概念
1. 方程
含有未知数的等式叫方程.方程中只含有一个未知数,并且未知数的指数是l,这样的方程叫一元一次方程,其一般形式为ax +b = 0 (a、b为常数,且a≠0);方程中含有两个未知数(x和y),并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程,一般形式:ax+by+c=o(a≠0, b≠0).
2.方程的解
能够使方程左右两边相等的未知数的值是方程的解.一般地,一元一次方程有唯一解,二元一次方程有无数组解,二元一次方程组有唯一解.
知识点三、 一元一次方程、二元一次方程的解法、步骤
1. 解一元一次方程的步骤
变形名称 具体做法 注意事项
去分母 在方程的两边同乘以各分母的最小公倍数 (1)不要漏乘不含分母的项(2)分子是一个整体,去分母后应加括号
去括号 先去小括号,再去中括号,最后去大括号(或由外向内) (1)不要漏乘括号里的项(2)注意“+”“-”号的改变
移项 把含有未知数的项都移到方程的另一边 (1)移项要变号(2)不要漏掉项
合并同类项 把方程化为ax=b(a≠0)的形式 字母及其指数不变,系数相加
系数化为1 在方程两边都乘以未知数的系数a,的得到方程的解 不要把分子、分母位置颠倒
2. 二元一次方程组的解法
解二元一次方程组的基本思想是“消元”,将“二元”转化为“一元”。通常的方法有:代入消元法和加减消元法.
代人消元法:把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代人另一个方程,实现消元,进而求得这个二元一次方程组的解,简称代人法.
加减消元法:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,简称加减法.
其实二元一次方程组的解法还有图像法,两个一次函数的交点坐标就是两个解析式联立方程组的解.
知识点四、列方程解应用题的一般步骤
列方程解决实际问题通常有下列几个步骤:
①审:审题,分析题中已知什么,求什么,明确各数量之间的关系
②设:设未知数,用字母表示适当是未知数.
③找:找出能够表示应用题全部意义的一个相等关系.
④列:根据题中的相等关系列出方程.
⑤解:解方程,求出未知数的值
⑥答:检验所得解是否符合题意,写出问题的答案.
重点例题解析
例1. (滨州)把方程变形为x=2,其依据是( )
A.等式的性质1 B.等式的性质2
C.分式的基本性质 D.不等式的性质1
例2. (孝感)已知是二元一次方程组的解,则的值是( )
A. B. C. D.
例3.(毕节)若与可以合并成一项,则的值是( )
A.2 B.0 C.-1 D.1
例4. (达州)如图,已知函数y=ax+b和y=cx+d的图象交于点M,则根据图象可知,关于x,y的二元一次方程组 的解为 .
例5. 解下列方程(组)
(1) (2)
例6. (福州)把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本则还缺25本.这个班有多少学生?
例7. (凉山州)根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 cm,放入一个大球水面升高 cm;
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
巩固练习
1. 已知mx=my,下列结论错误的是( )
A.x=y B.a+mx=a+my C.mx-y=my-y D.amx=amy
2. (泰安)方程与下列方程构成的方程组的解为的是( )
A. B. C. D.
3. (莆田)若x、y满足方程组,则x —y的值等于( )
A.—1 B.1 C.2 D.3
4. (恩施)“六一”期间,某商店将单价标为130元的书包按8折出售可获得30%,该书包每个的进价是( )
A.65元 B.80元 C.100元 D. 104元
5. (娄底)已知关于x的方程2x+a-5=0的解是x=2,则a的值为____________.
6. (徐州)函数y=2x与y=x+1的图象的交点坐标为 .
7. (宁夏)若2a-b=5,a-2b=4,则a-b的值为______.
8. 解下列方程(组)
(1)解方程: (2) 解方程组 eq \b\lc\{()
9. (齐齐哈尔)将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有 ( )
A.6种 B.7种 C.8种 D.9种
10. 如图,用10块相同的长方形纸板拼成一个矩形,设长方形纸板的长和宽分别为xcm和ycm,则依题意列方程式组正确的是( )
A B C D
11. (宁波)用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和 2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用 A方法,其余用 B方法.
(1)用 x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若栽剪出的侧面和底面恰好全部用完,问能做多少个盒子?
12.(南昌)小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.
妈妈:“今天买这两样菜共花了45元,上月买同重量的这两种菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨了50%,排骨的单价上涨了20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).
中考预测
1. 方程组 的解为( )
A. B. C. D.
2. 已知是方程组的解,则a-b的值是( )
A.-1 B.2 C.3 D.4
3. 若,则实数a在数轴上的对应点一定在( )
A.原点左侧 B.原点或原点左侧 C.原点右侧 D.原点或原点右侧
4. 已知,则x+y的值为( )
A.0 B.-1 C.1 D.5
5. 由方程组可得出x与y的关系是( )
A. B. C. D.
6.已知x、y是二元一次方程组的解,则代数式x2-4y2的值为 .
7. 如图,已知函数y=2x+b与函数y=kx-3的图象交于点P,则方程组 的解是 .
8.哥哥与弟弟的年龄和是18岁,弟弟对哥哥说:“当我的年龄是你现在年龄的时候,你就是
18岁,”如果现在弟弟的年龄是x岁,哥哥的年龄是y岁,根据题意列出方程组
是 .
9.今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3
分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数
是所负场数的整数倍,则小虎足球队所负场数的情况有( )
A. 2种 B. 3种 C. 4种 D. 5 种
10.情境:
试根据图中的信息,解答下列问题:
购买6根跳绳需 元,购买12根跳绳需 元;
小红比小明多买2根,付款时小红反而比小明少5元.你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
11.如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”.现向容器内匀速注水,注满为止.在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为____________cm,匀速注水的水流速度为__________cm/s;
(2)若“几何体”的下方圆柱的底面积为15cm,求“几何体”上方圆柱的高和底面积.
12.几个小伙伴打算去音乐厅观看演出,他们准备用360元钱购买门票.下面是两个小伙伴的对话:
根据对话中的信息,请你求出小伙伴们的人数.
中考预测
PAGE
- 13 -
同课章节目录
