2023—2024学年北师大版数学八年级上册 第1章勾股定理 自主提升训练 (含解析)
文档属性
| 名称 | 2023—2024学年北师大版数学八年级上册 第1章勾股定理 自主提升训练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 497.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 08:17:37 | ||
图片预览




文档简介
2023-2024学年北师大版八年级数学上册《第1章勾股定理》
单元自主提升训练(附答案)
一、单选题
1.已知a、b、c分别为中,,的对边,下列说法错误的是( )
A.,则 B.,则
C.,则 D.总有
2.下面四组数中是勾股数的有( )
①,,;②,,;③,,;④,,.
A.组 B.组 C.组 D.组
3.若一直角三角形两边长分别为12和5,则第三边长的平方是( )
A.169 B.169或119 C.13或15 D.15
4.如图,在中,,,,点是上的动点,则的最小值为( )
A.5 B. C. D.6
5.如图,已知中,,,将此三角形沿翻折,使得点A与点B重 合,则的长为( )
A.3 B.4 C.5 D.6
6.中,,,高,则的长为( )
A.4 B.14 C.5 或 9 D.4 或 14
7.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为,较短直角边长为.若,大正方形的面积为36,则小正方形的边长为( )
A.9 B.6 C.4 D.3
8.我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiā)生其中,出水一尺.引葭赴岸,适与岸齐.问水深几何.”(丈、尺是长度单位,1丈尺)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度是多少?则水深为( )
A.10尺 B.12尺 C.13尺 D.15尺
二、填空题
9.在中,,边上的高为15,则的面积是 .
10.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面3米C处折断,树尖B恰好碰到地面,经测量米,则树原高为 米.
11.如图,它是由弦图变化得到的,是由八个全等的直角三角形拼接而成的,将图中正方形、正方形、正方形的面积分别记为、、.
(1)若,,则 .
(2)若,则 .
12.如图,一圆柱体的底面周长为,高为,是直径,一只蚂蚁从点出发沿着圆柱的表面爬行到点的最短路程为 .
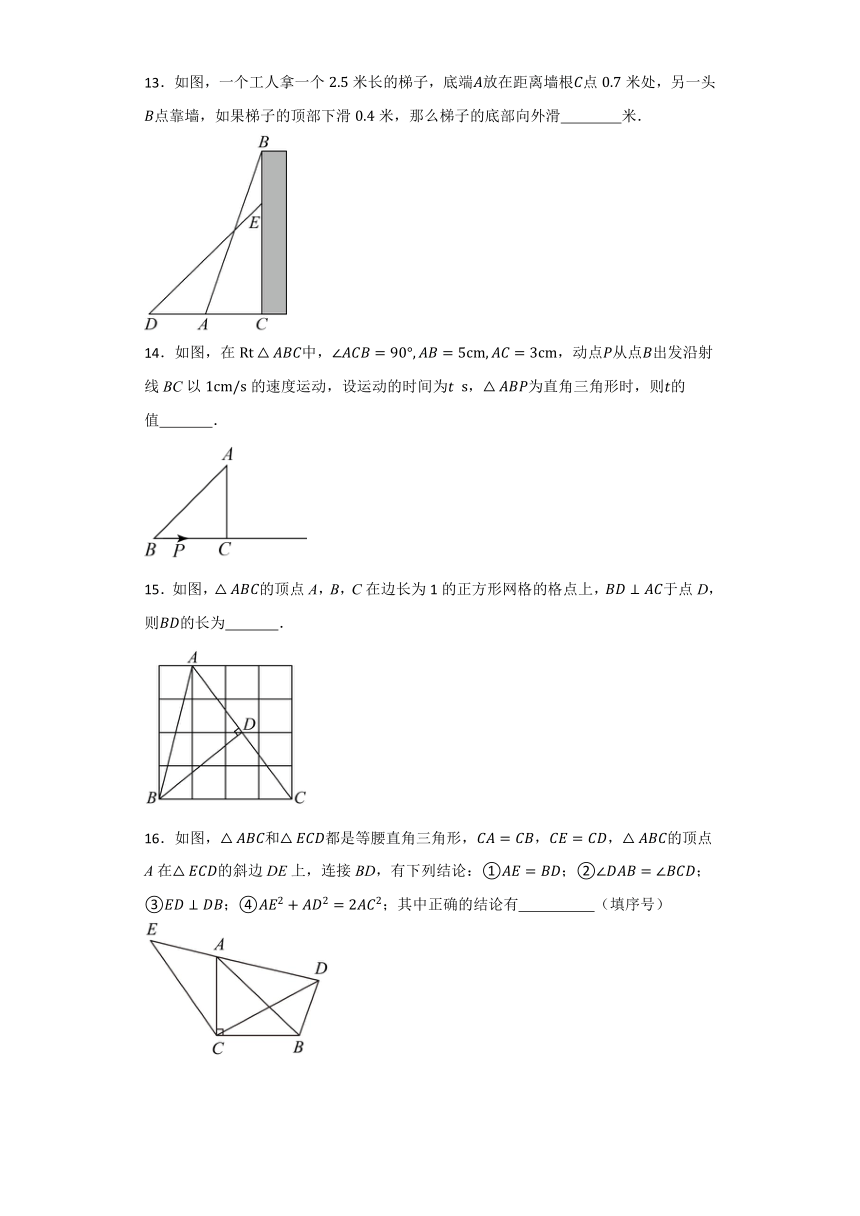
13.如图,一个工人拿一个米长的梯子,底端放在距离墙根点米处,另一头点靠墙,如果梯子的顶部下滑米,那么梯子的底部向外滑 米.
14.如图,在中,,动点从点出发沿射线BC以的速度运动,设运动的时间为 ,为直角三角形时,则的值 .
15.如图,的顶点A,B,C在边长为1的正方形网格的格点上,于点D,则的长为 .
16.如图,和都是等腰直角三角形,,的顶点A在的斜边DE上,连接BD,有下列结论:①;②;③;④;其中正确的结论有 (填序号)
三、解答题
17.如下图,在中,,于点,.
(1)求的面积;
(2)求线段的长.
18.如图,一辆小汽车在一条限速的公路上沿直线行驶,某一时刻刚好行驶到路面车速检测仪的正前方处的点,过了后,测得小汽车所在的点与车速检测仪之间的距离为.
(1)求,间的距离;
(2)这辆小汽车超速了吗?请说明理由.
19.如图,某人从地到地共有三条路可选,第一条路是从地沿到达地,为10米,第二条路是从地沿折线到达地,为8米,为6米,第三条路是从地沿折线到达地共行走26米,若刚好在一条直线上.
(1)求证:;
(2)求和的长.
20.根据山西省教育厅“2023年度基础教育领域重点工作推进会”要求,扎实推进建设100所公办幼儿园任务落实,某地计划要在如图所示的直线上,新建一所幼儿园,该区域有两个小区所在的位置在点和点处,于A,于B.已知,,求该幼儿园应该建在距点A为多少处,可以使两个小区到幼儿园的距离相等.
21.已知四边形中,,为中点,且,,.
(1)求的值;
(2)求直线与直线的距离.
22.在本学期的数学学习中,老师提出了这样一个问题:
如图1,在中,,D是的中点,求边上的中线的取值范围.
【阅读理解】
小明在班内经过合作交流,得到了如下的解决方法:
(1)如图1,延长到M,使,连接,根据______可以判定,得出,这样就能把线段、、集中在中,利用三角形三边的关系,即可得出中线的取值范围.
【方法感悟】
我们发现,几何图形中出现能表示相等数量关系的条件时,如:“中点”、“角平分线”等,往往可以考虑做“辅助线”,构造全等三角形,从而达到解决问题的目的.
【问题解决】
(2)如图2,在中,,的平分线交边于点D,若,求的长.
【应用提升】
(3)已知:如图3,中,.D、E是三角形边、上两个动点,且,连接,求的最小值.
23.著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为),也可以表示为,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路,且.测得千米,千米,求新路比原路少多少千米?
(3)在第(2)问中若时,,,,,设,求x的值.
参考答案
1.解:由题意可得,
,则,正确不符合题意;
,则,正确不符合题意;
,则,正确不符合题意;
未说明直角,错误,故符合题意;
故选D;
2.解:①,,;②,,;④,,不是整数,故不符合题意;
③三边是整数,同时能构成直角三角形,故符合题意;
故选:A.
3.解:当边长为12的边为直角边时,则第三边的长的平方为;
当边长为12的边为斜边时,则第三边的长的平方为;
综上所述,第三边长的平方是169或119,
故选B.
4.解:∵在中,,,,
∴,
当时,取得最小值,
∴,
故选:C.
5.解:∵三角形沿翻折,使得点A与点B重 合,
∴,
∵,
∴,
在中,
∴,
解得,
故选:C.
6.解:如图1,当点D在线段上时,
锐角中,,,.
在中,,
由勾股定理得:,则.
在中,,
由勾股定理得:,则,
故的长为;
如图2,当点D在线段的延长线上时,
钝角中,,,边上高.
在中,,
由勾股定理得:,则.
在中,,
由勾股定理得:,则,
故的长为.
综上可得BC的长为4或14.
故选:D.
7.解:由题意可知:中间小正方形的边长为:,
∴小正方形的面积等于:,
∵每一个直角三角形的面积为:,
∴,
∴,
∵,
∴,
故选:C.
8.解: 设水深为h尺,则芦苇高为尺,
由题意知芦苇距离水池一边的距离为尺,
根据勾股定理得:,
解得,
即水深为12尺,
故选:B.
9.解:①当点D在上时,如图:
由题意,得:,,,
∴
∴,
∴的面积是;
②当点D不在上时,如图:
由题意,得:,,,
∴
∴,
∴的面积是;
综上:的面积是或.
10.解:根据题意得:米,米,,
由勾股定理得, 米,
所以米.
故答案为8.
11.解:(1)当,时,
正方形的边长,正方形的边长,
根据题意,该图形由八个全等的直角三角形拼接而成,
由全等的直角三角的性质可得,,
设,则,,
∴,解得,
∴,,
∴在中,,
∴正方形的面积;
故答案为:13;
(2)设每一个直角三角形面积为,
∴则,,
∵,
∴,
解得.
故答案为:8.
12.解:如图所示:由于圆柱体的底面周长为,
,
,
,
故答案为:13.
13.解:米,米,
米,
梯子的顶部下滑米,
米,
米,
米,
梯子的底部向外滑出,
米.
故答案是:.
14.解:在中,由勾股定理得:,
,
由题意得:.,
①当为直角时,
如图①,点与点重合,
,
;
②当为直角时,
如图②,.,,
在中,,
在中,,
即,
解得,
故答案为:或.
15.解:如图,,,
∴的面积,
由勾股定理得,
则,
解得,
故答案为:
16.解:∵和都是等腰直角三角形,
∴,
∴,即:,
∵,
∴,
∴,故①正确;
由三角形外角定理,,
∵,
∴,
∵,
∴,
∵,
∴,故②正确;
∵,
∴,
∵,
∴,
即:,故③正确;
∵,
∴在中,,
∵为等腰直角三角形,
∴,
∴,
∵,
∴,故④正确;
故答案为:①②③④.
17.(1)解:在中,, ,
∴,
∴,
∴的面积为.
(2)解:∵在中,,于点,
∴,
∵,
∴,
解得,
∴线段的长为.
18.(1)解:在中,由,,且为斜边,
根据勾股定理可得.
答:,间的距离为.
(2)解:这辆小汽车没有超速,理由如下:
,
而,
,
所以这辆小汽车没有超速.
19.(1)证明:∵米,米,米,
∴,
∴是直角三角形,即;
(2)解:设米,则米,
∴(米),
在中,由勾股定理得:,
解得:,则.
答:的长为17米,的长为9米.
20.解:由题意,设,则.
∵在中,,
∴.
∵在中,,
∴.
∵,
∴,即,
解得:.
答:该幼儿园E应该建在距点A为1km处,可以使两个小区到幼儿园的距离相等.
21.(1)解:延长交的延长线于点,如图,
,
,,
为中点,
,
在与中,
,
,
,,
,
,
,
;
(2)过点作,如图,
,,
,
.
22.解:(1)∵D是的中点,
∴,
在和中,
∵,
∴,
故答案为:;
(2)延长到P,使,连接,
∴,
∴,
∴,
∵,
∴,
∵的平分线为,
∴,
又∵,
∴,
∴;
(3)过点C向上方作,使,连接,过点M作,交的延长线于点N,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
∵,
∴,
∴,
∴,当点B、E、M在同一直线上时,的值最小,即最小值为,
在中,
∵,
∴,
∴,
在中,由勾股定理可得,
即的最小值为10.
23.(1)解:梯形的面积为,
也可以表示为,
∴,
即;
(2)∵,
∴,
在中,,
即,
解得,
即,
(千米),
答:新路比原路少0.05千米;
(3)设,则,
在中,,
在中,,
∴,
即,
解得:.
单元自主提升训练(附答案)
一、单选题
1.已知a、b、c分别为中,,的对边,下列说法错误的是( )
A.,则 B.,则
C.,则 D.总有
2.下面四组数中是勾股数的有( )
①,,;②,,;③,,;④,,.
A.组 B.组 C.组 D.组
3.若一直角三角形两边长分别为12和5,则第三边长的平方是( )
A.169 B.169或119 C.13或15 D.15
4.如图,在中,,,,点是上的动点,则的最小值为( )
A.5 B. C. D.6
5.如图,已知中,,,将此三角形沿翻折,使得点A与点B重 合,则的长为( )
A.3 B.4 C.5 D.6
6.中,,,高,则的长为( )
A.4 B.14 C.5 或 9 D.4 或 14
7.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为,较短直角边长为.若,大正方形的面积为36,则小正方形的边长为( )
A.9 B.6 C.4 D.3
8.我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiā)生其中,出水一尺.引葭赴岸,适与岸齐.问水深几何.”(丈、尺是长度单位,1丈尺)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度是多少?则水深为( )
A.10尺 B.12尺 C.13尺 D.15尺
二、填空题
9.在中,,边上的高为15,则的面积是 .
10.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面3米C处折断,树尖B恰好碰到地面,经测量米,则树原高为 米.
11.如图,它是由弦图变化得到的,是由八个全等的直角三角形拼接而成的,将图中正方形、正方形、正方形的面积分别记为、、.
(1)若,,则 .
(2)若,则 .
12.如图,一圆柱体的底面周长为,高为,是直径,一只蚂蚁从点出发沿着圆柱的表面爬行到点的最短路程为 .
13.如图,一个工人拿一个米长的梯子,底端放在距离墙根点米处,另一头点靠墙,如果梯子的顶部下滑米,那么梯子的底部向外滑 米.
14.如图,在中,,动点从点出发沿射线BC以的速度运动,设运动的时间为 ,为直角三角形时,则的值 .
15.如图,的顶点A,B,C在边长为1的正方形网格的格点上,于点D,则的长为 .
16.如图,和都是等腰直角三角形,,的顶点A在的斜边DE上,连接BD,有下列结论:①;②;③;④;其中正确的结论有 (填序号)
三、解答题
17.如下图,在中,,于点,.
(1)求的面积;
(2)求线段的长.
18.如图,一辆小汽车在一条限速的公路上沿直线行驶,某一时刻刚好行驶到路面车速检测仪的正前方处的点,过了后,测得小汽车所在的点与车速检测仪之间的距离为.
(1)求,间的距离;
(2)这辆小汽车超速了吗?请说明理由.
19.如图,某人从地到地共有三条路可选,第一条路是从地沿到达地,为10米,第二条路是从地沿折线到达地,为8米,为6米,第三条路是从地沿折线到达地共行走26米,若刚好在一条直线上.
(1)求证:;
(2)求和的长.
20.根据山西省教育厅“2023年度基础教育领域重点工作推进会”要求,扎实推进建设100所公办幼儿园任务落实,某地计划要在如图所示的直线上,新建一所幼儿园,该区域有两个小区所在的位置在点和点处,于A,于B.已知,,求该幼儿园应该建在距点A为多少处,可以使两个小区到幼儿园的距离相等.
21.已知四边形中,,为中点,且,,.
(1)求的值;
(2)求直线与直线的距离.
22.在本学期的数学学习中,老师提出了这样一个问题:
如图1,在中,,D是的中点,求边上的中线的取值范围.
【阅读理解】
小明在班内经过合作交流,得到了如下的解决方法:
(1)如图1,延长到M,使,连接,根据______可以判定,得出,这样就能把线段、、集中在中,利用三角形三边的关系,即可得出中线的取值范围.
【方法感悟】
我们发现,几何图形中出现能表示相等数量关系的条件时,如:“中点”、“角平分线”等,往往可以考虑做“辅助线”,构造全等三角形,从而达到解决问题的目的.
【问题解决】
(2)如图2,在中,,的平分线交边于点D,若,求的长.
【应用提升】
(3)已知:如图3,中,.D、E是三角形边、上两个动点,且,连接,求的最小值.
23.著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为),也可以表示为,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路,且.测得千米,千米,求新路比原路少多少千米?
(3)在第(2)问中若时,,,,,设,求x的值.
参考答案
1.解:由题意可得,
,则,正确不符合题意;
,则,正确不符合题意;
,则,正确不符合题意;
未说明直角,错误,故符合题意;
故选D;
2.解:①,,;②,,;④,,不是整数,故不符合题意;
③三边是整数,同时能构成直角三角形,故符合题意;
故选:A.
3.解:当边长为12的边为直角边时,则第三边的长的平方为;
当边长为12的边为斜边时,则第三边的长的平方为;
综上所述,第三边长的平方是169或119,
故选B.
4.解:∵在中,,,,
∴,
当时,取得最小值,
∴,
故选:C.
5.解:∵三角形沿翻折,使得点A与点B重 合,
∴,
∵,
∴,
在中,
∴,
解得,
故选:C.
6.解:如图1,当点D在线段上时,
锐角中,,,.
在中,,
由勾股定理得:,则.
在中,,
由勾股定理得:,则,
故的长为;
如图2,当点D在线段的延长线上时,
钝角中,,,边上高.
在中,,
由勾股定理得:,则.
在中,,
由勾股定理得:,则,
故的长为.
综上可得BC的长为4或14.
故选:D.
7.解:由题意可知:中间小正方形的边长为:,
∴小正方形的面积等于:,
∵每一个直角三角形的面积为:,
∴,
∴,
∵,
∴,
故选:C.
8.解: 设水深为h尺,则芦苇高为尺,
由题意知芦苇距离水池一边的距离为尺,
根据勾股定理得:,
解得,
即水深为12尺,
故选:B.
9.解:①当点D在上时,如图:
由题意,得:,,,
∴
∴,
∴的面积是;
②当点D不在上时,如图:
由题意,得:,,,
∴
∴,
∴的面积是;
综上:的面积是或.
10.解:根据题意得:米,米,,
由勾股定理得, 米,
所以米.
故答案为8.
11.解:(1)当,时,
正方形的边长,正方形的边长,
根据题意,该图形由八个全等的直角三角形拼接而成,
由全等的直角三角的性质可得,,
设,则,,
∴,解得,
∴,,
∴在中,,
∴正方形的面积;
故答案为:13;
(2)设每一个直角三角形面积为,
∴则,,
∵,
∴,
解得.
故答案为:8.
12.解:如图所示:由于圆柱体的底面周长为,
,
,
,
故答案为:13.
13.解:米,米,
米,
梯子的顶部下滑米,
米,
米,
米,
梯子的底部向外滑出,
米.
故答案是:.
14.解:在中,由勾股定理得:,
,
由题意得:.,
①当为直角时,
如图①,点与点重合,
,
;
②当为直角时,
如图②,.,,
在中,,
在中,,
即,
解得,
故答案为:或.
15.解:如图,,,
∴的面积,
由勾股定理得,
则,
解得,
故答案为:
16.解:∵和都是等腰直角三角形,
∴,
∴,即:,
∵,
∴,
∴,故①正确;
由三角形外角定理,,
∵,
∴,
∵,
∴,
∵,
∴,故②正确;
∵,
∴,
∵,
∴,
即:,故③正确;
∵,
∴在中,,
∵为等腰直角三角形,
∴,
∴,
∵,
∴,故④正确;
故答案为:①②③④.
17.(1)解:在中,, ,
∴,
∴,
∴的面积为.
(2)解:∵在中,,于点,
∴,
∵,
∴,
解得,
∴线段的长为.
18.(1)解:在中,由,,且为斜边,
根据勾股定理可得.
答:,间的距离为.
(2)解:这辆小汽车没有超速,理由如下:
,
而,
,
所以这辆小汽车没有超速.
19.(1)证明:∵米,米,米,
∴,
∴是直角三角形,即;
(2)解:设米,则米,
∴(米),
在中,由勾股定理得:,
解得:,则.
答:的长为17米,的长为9米.
20.解:由题意,设,则.
∵在中,,
∴.
∵在中,,
∴.
∵,
∴,即,
解得:.
答:该幼儿园E应该建在距点A为1km处,可以使两个小区到幼儿园的距离相等.
21.(1)解:延长交的延长线于点,如图,
,
,,
为中点,
,
在与中,
,
,
,,
,
,
,
;
(2)过点作,如图,
,,
,
.
22.解:(1)∵D是的中点,
∴,
在和中,
∵,
∴,
故答案为:;
(2)延长到P,使,连接,
∴,
∴,
∴,
∵,
∴,
∵的平分线为,
∴,
又∵,
∴,
∴;
(3)过点C向上方作,使,连接,过点M作,交的延长线于点N,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
∵,
∴,
∴,
∴,当点B、E、M在同一直线上时,的值最小,即最小值为,
在中,
∵,
∴,
∴,
在中,由勾股定理可得,
即的最小值为10.
23.(1)解:梯形的面积为,
也可以表示为,
∴,
即;
(2)∵,
∴,
在中,,
即,
解得,
即,
(千米),
答:新路比原路少0.05千米;
(3)设,则,
在中,,
在中,,
∴,
即,
解得:.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
