2023—2024学年北师大版数学八年级上册1.2一定是直角三角形吗 自主提升训练 (含解析)
文档属性
| 名称 | 2023—2024学年北师大版数学八年级上册1.2一定是直角三角形吗 自主提升训练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 571.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-29 09:31:20 | ||
图片预览


文档简介
2023-2024学年北师大版八年级数学上册《1.2一定是直角三角形吗》
自主提升训练(附答案)
一、单选题
1.下列条件中,不能说明是直角三角形的是( )
A. B.
C. D.
2.下面图形能够验证勾股定理的有( )个
A.4 B.3 C.2 D.1
3.在认识了勾股定理的赵爽弦图后,一位同学尝试将个全等的小正方形嵌入长方形内部,其中点,,,分别在长方形的边,,和上,若,,则小正方形的边长为( )
A. B. C. D.
4.如图,长为的梯子靠在墙上,梯子的底端离墙脚线的距离为,则梯子顶端的高度h是( )
A. B. C. D.
5.如图,两个边长为1的正方形整齐地排在数轴上形成一个大的长方形,以O点为圆心,以长方形的对角线为半径作圆与数轴有两个交点,其中点Р表示的数是( )
A. B. C.2.2 D.
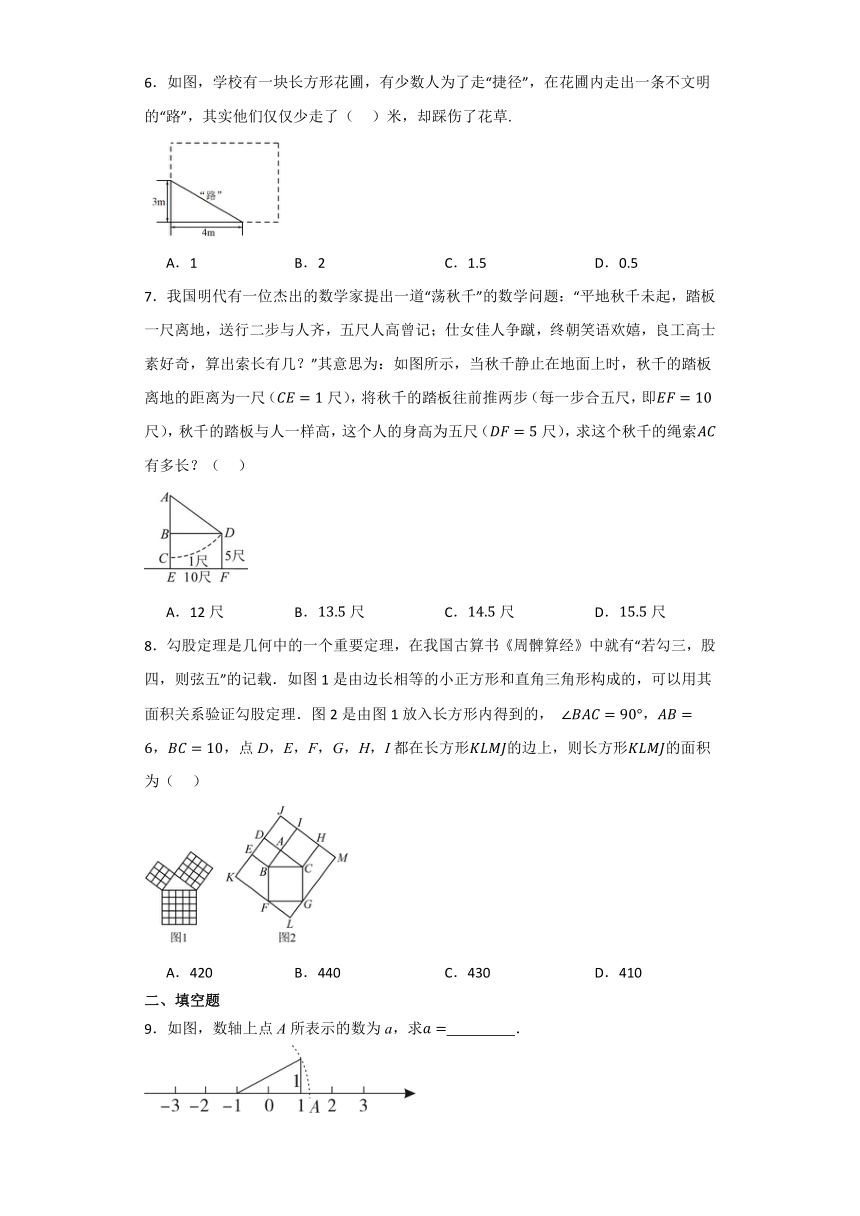
6.如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,其实他们仅仅少走了( )米,却踩伤了花草.
A.1 B.2 C.1.5 D.0.5
7.我国明代有一位杰出的数学家提出一道“荡秋千”的数学问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索长有几?”其意思为:如图所示,当秋千静止在地面上时,秋千的踏板离地的距离为一尺(尺),将秋千的踏板往前推两步(每一步合五尺,即尺),秋千的踏板与人一样高,这个人的身高为五尺(尺),求这个秋千的绳索有多长?( )
A.12尺 B.尺 C.尺 D.尺
8.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的, ,点D,E,F,G,H,I都在长方形的边上,则长方形的面积为( )
A.420 B.440 C.430 D.410
二、填空题
9.如图,数轴上点A所表示的数为a,求 .
10.如图,直线l上有三个边长分别为a,b,c的正方形,则有 (填“>”或“<”或“”)
11.新冠疫情防控过程中,某中学在大门口的正上方处装着一个红外线激光测温仪,离地米(如图所示),一个身高米的学生(米)正对门缓慢走到离门米的地方时(米),测温仪自动显示体温,则人头顶离测温仪的距离等于 .
12.在如图所示的图形中,所有四边形都是正方形,所有三角形都是直角三角形,若正方形、、 的面积依次为5、6、20,则正方形的面积是 .
13.如图,一只蚂蚁要从A处沿圆柱体的侧面爬到B处,已知圆柱体的高是8,底面周长是12,则蚂蚁爬行的最短路程为 .
14.“赵爽弦图”是2002年在北京召开的国际数学家大会的会徽,它与数学中著名的勾股定理有着密切关系.在学完我国古代著名的“赵爽弦图”的示意图后,我校某同学想在逐梦运动场规划出一块活动场地,如图所示,现规划土地由四个全等的直角三角形拼接而成,其中,,则的长是 m.
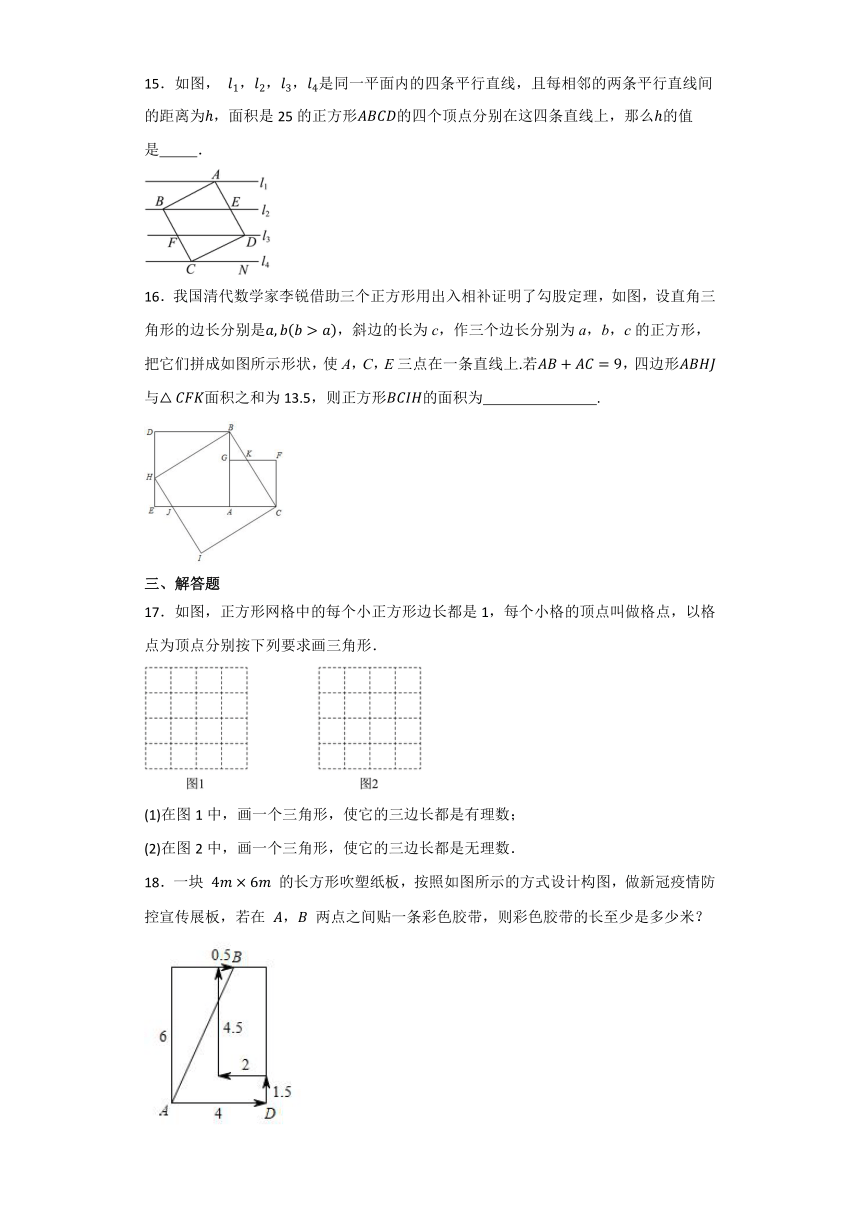
15.如图, 是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为,面积是25的正方形的四个顶点分别在这四条直线上,那么的值是 .
16.我国清代数学家李锐借助三个正方形用出入相补证明了勾股定理,如图,设直角三角形的边长分别是,斜边的长为c,作三个边长分别为a,b,c的正方形,把它们拼成如图所示形状,使A,C,E三点在一条直线上.若,四边形与面积之和为13.5,则正方形的面积为 .
三、解答题
17.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数;
(2)在图2中,画一个三角形,使它的三边长都是无理数.
18.一块 的长方形吹塑纸板,按照如图所示的方式设计构图,做新冠疫情防控宣传展板,若在 两点之间贴一条彩色胶带,则彩色胶带的长至少是多少米?
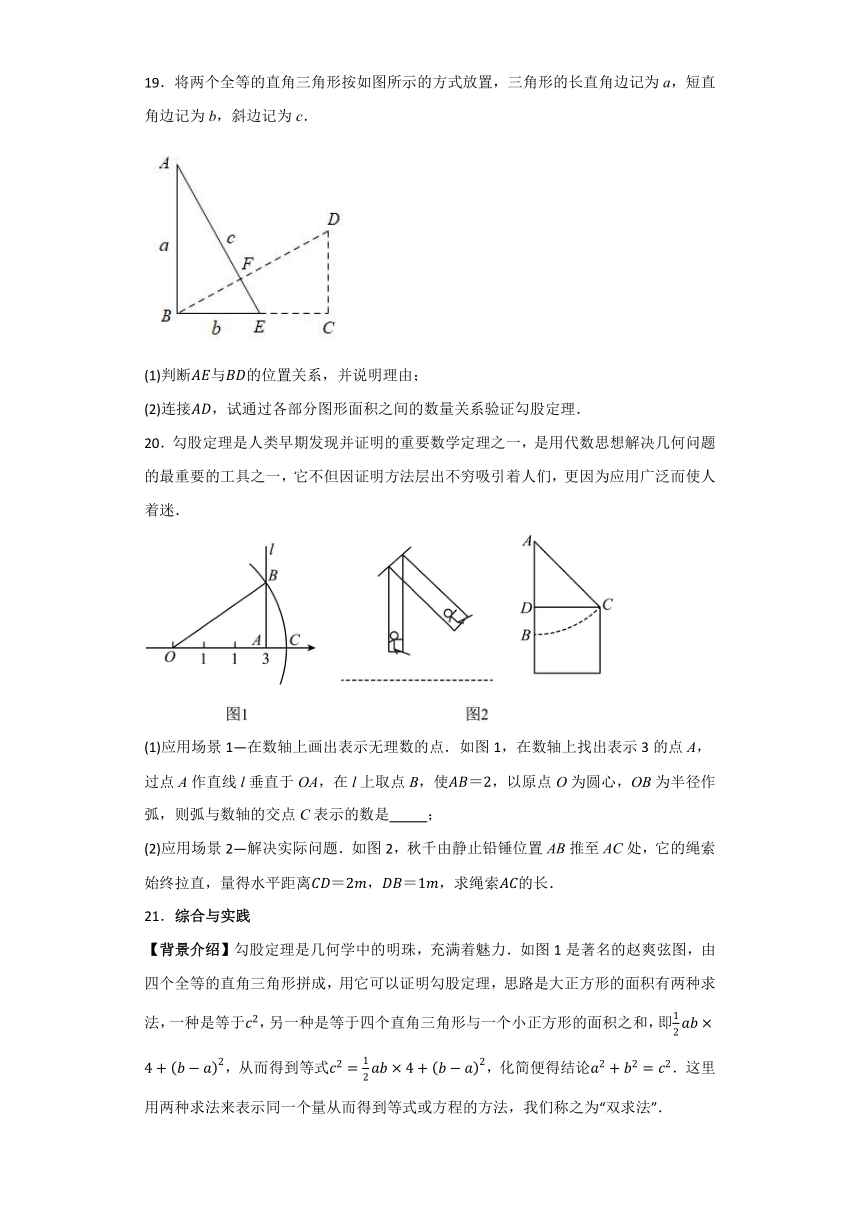
19.将两个全等的直角三角形按如图所示的方式放置,三角形的长直角边记为a,短直角边记为b,斜边记为c.
(1)判断与的位置关系,并说明理由;
(2)连接,试通过各部分图形面积之间的数量关系验证勾股定理.
20.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人着迷.
(1)应用场景1—在数轴上画出表示无理数的点.如图1,在数轴上找出表示3的点A,过点A作直线l垂直于OA,在l上取点B,使,以原点O为圆心,OB为半径作弧,则弧与数轴的交点C表示的数是 ;
(2)应用场景2—解决实际问题.如图2,秋千由静止铅锤位置AB推至AC处,它的绳索始终拉直,量得水平距离,求绳索的长.
21.综合与实践
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得结论.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
【方法运用】千百年来,人们对勾股定理的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者.向常春在2010年构造发现了一个新的证法:把两个全等的直角三角形和如图2放置,其三边长分别为,,,,显然.
(1)请用,,分别表示出四边形,梯形,的面积,再探究这三个图形面积之间的关系,证明勾股定理.
(2)【方法迁移】请利用“双求法”解决下面的问题:如图3,小正方形边长为1,连接小正方形的三个顶点,可得,则边上的高为______.
(3)如图4,在中,是边上的高,,,,设,求的值.
参考答案
1.解:A.,且,,故是直角三角形;
B.,且,,,,故不是直角三角形;
C.,,故是直角三角形;
D.,可设,,,,,故是直角三角形.
故选B.
2.解:第一个图形:两个小正方形的面积分别为4和9,大正方形的面积为13,可得,可得,可以验证勾股定理.
第二个图形:梯形的面积,化简得;可以证明勾股定理.
第三个图形:中间小正方形的面积;化简得,可以证明勾股定理.
第四个图形:由图形可知割补前后的两个小直角三角形全等,则正方形的面积两个直角三角形的面积的和,即,化简得;可以证明勾股定理,
能够验证勾股定理的有4个.
故选:A.
3.解:如图所示,根据赵爽弦图,将小正方形分成4个全等的直角三角形,和一个最小的正方形,
设直角三角形的短直角边长为,长直角边为,则正方形的水平宽度与垂直高度为,
依题意,
解得:
∴小正方形的边长为:,
故选:A.
4.解:由题意得,,
故选B.
5.解:∵,
∴点Р表示的数是.
故选D.
6.解:如图,在中,已知,所以,
所以他们仅仅少走了.
故选:
7.解:设绳索有x尺长,
则,
解得:.
故选:C.
8.解:如图,延长交于P,延长交于Q,
由题意得,,
∴,
∴,
∴,
同理可证,
∴,
∵图2是由图1放入长方形内得到,
∴,,
∴长方形的面积.
故选:B.
9.解:
解:如图,由勾股定理得
.
∵点C表示-1,
∴点A表示的数是.
故答案为:.
10.解:如图,
∵正方形a,c的边长分别为a和c,
∴,,
由正方形的性质得:,,
∵,,
∴,
在和中,,
∴,
∴,
∴,
∴正方形b的面积为,
即,
故答案为:.
11.解:如图,
过点作于点,
∵米,米,米,
∴米,
在中,由勾股定理得到:(米);
故答案是:米.
12.解:由题意:,,
正方形、、的面积依次为5、6、20,
,
.
故答案为:9.
13.解:根据题意,将圆柱展开如下:
∴,
∴,
∴最短路程为10,
故答案为:10.
14.解:∵,,即直角三角形的两直角边长为,
∴小正方形的边长为,
∴.
故答案为:
15.解:过点作交于点,交于点,
在正方形中,
又
∵正方形的面积为25,
或(舍去)
故答案为:
16.解:如图,作于点,则,
四边形、四边形、四边形都是正方形,
,,,
,
,
,,
,,,
,
,,
,
,,
,
,
,
,
,
,
,,
,
,
,
①,
,
②,
由①②得,
,
,
故答案为:36.
17.(1)解:如图,即为所求;(答案不唯一)
此时:;
(2)解:如图,即为所求;(答案不唯一)
此时:.
18.解:点C位置如图,
则 ,,
在直角 中, ,
答:彩色胶带的长至少是 .
19.(1)解:;
理由:∵,
∴,
∴,
∴,
即;
(2)解:连接,,
∵,
∴,,,
∴,
又∵
,
∴ ,
整理得: .
20.解:(1)在中,OB===,
∴,
∴点C表示的数是,
故答案为:;
(2)解:设秋千绳索AC的长度为,
由题意可得AC=AB=,
∵,
∴,
在中,,
∴,
解得,
即AC的长度为,
答:绳索AC的长为.
21.(1)证明:∵,,,
∴
∴
∴
(2),
,
,
即AB边上的高是
(3)解:在中,由勾股定理得
∵,
∴
在中,由勾股定理得
∴,
∴
自主提升训练(附答案)
一、单选题
1.下列条件中,不能说明是直角三角形的是( )
A. B.
C. D.
2.下面图形能够验证勾股定理的有( )个
A.4 B.3 C.2 D.1
3.在认识了勾股定理的赵爽弦图后,一位同学尝试将个全等的小正方形嵌入长方形内部,其中点,,,分别在长方形的边,,和上,若,,则小正方形的边长为( )
A. B. C. D.
4.如图,长为的梯子靠在墙上,梯子的底端离墙脚线的距离为,则梯子顶端的高度h是( )
A. B. C. D.
5.如图,两个边长为1的正方形整齐地排在数轴上形成一个大的长方形,以O点为圆心,以长方形的对角线为半径作圆与数轴有两个交点,其中点Р表示的数是( )
A. B. C.2.2 D.
6.如图,学校有一块长方形花圃,有少数人为了走“捷径”,在花圃内走出一条不文明的“路”,其实他们仅仅少走了( )米,却踩伤了花草.
A.1 B.2 C.1.5 D.0.5
7.我国明代有一位杰出的数学家提出一道“荡秋千”的数学问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索长有几?”其意思为:如图所示,当秋千静止在地面上时,秋千的踏板离地的距离为一尺(尺),将秋千的踏板往前推两步(每一步合五尺,即尺),秋千的踏板与人一样高,这个人的身高为五尺(尺),求这个秋千的绳索有多长?( )
A.12尺 B.尺 C.尺 D.尺
8.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的, ,点D,E,F,G,H,I都在长方形的边上,则长方形的面积为( )
A.420 B.440 C.430 D.410
二、填空题
9.如图,数轴上点A所表示的数为a,求 .
10.如图,直线l上有三个边长分别为a,b,c的正方形,则有 (填“>”或“<”或“”)
11.新冠疫情防控过程中,某中学在大门口的正上方处装着一个红外线激光测温仪,离地米(如图所示),一个身高米的学生(米)正对门缓慢走到离门米的地方时(米),测温仪自动显示体温,则人头顶离测温仪的距离等于 .
12.在如图所示的图形中,所有四边形都是正方形,所有三角形都是直角三角形,若正方形、、 的面积依次为5、6、20,则正方形的面积是 .
13.如图,一只蚂蚁要从A处沿圆柱体的侧面爬到B处,已知圆柱体的高是8,底面周长是12,则蚂蚁爬行的最短路程为 .
14.“赵爽弦图”是2002年在北京召开的国际数学家大会的会徽,它与数学中著名的勾股定理有着密切关系.在学完我国古代著名的“赵爽弦图”的示意图后,我校某同学想在逐梦运动场规划出一块活动场地,如图所示,现规划土地由四个全等的直角三角形拼接而成,其中,,则的长是 m.
15.如图, 是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为,面积是25的正方形的四个顶点分别在这四条直线上,那么的值是 .
16.我国清代数学家李锐借助三个正方形用出入相补证明了勾股定理,如图,设直角三角形的边长分别是,斜边的长为c,作三个边长分别为a,b,c的正方形,把它们拼成如图所示形状,使A,C,E三点在一条直线上.若,四边形与面积之和为13.5,则正方形的面积为 .
三、解答题
17.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数;
(2)在图2中,画一个三角形,使它的三边长都是无理数.
18.一块 的长方形吹塑纸板,按照如图所示的方式设计构图,做新冠疫情防控宣传展板,若在 两点之间贴一条彩色胶带,则彩色胶带的长至少是多少米?
19.将两个全等的直角三角形按如图所示的方式放置,三角形的长直角边记为a,短直角边记为b,斜边记为c.
(1)判断与的位置关系,并说明理由;
(2)连接,试通过各部分图形面积之间的数量关系验证勾股定理.
20.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人着迷.
(1)应用场景1—在数轴上画出表示无理数的点.如图1,在数轴上找出表示3的点A,过点A作直线l垂直于OA,在l上取点B,使,以原点O为圆心,OB为半径作弧,则弧与数轴的交点C表示的数是 ;
(2)应用场景2—解决实际问题.如图2,秋千由静止铅锤位置AB推至AC处,它的绳索始终拉直,量得水平距离,求绳索的长.
21.综合与实践
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得结论.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
【方法运用】千百年来,人们对勾股定理的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者.向常春在2010年构造发现了一个新的证法:把两个全等的直角三角形和如图2放置,其三边长分别为,,,,显然.
(1)请用,,分别表示出四边形,梯形,的面积,再探究这三个图形面积之间的关系,证明勾股定理.
(2)【方法迁移】请利用“双求法”解决下面的问题:如图3,小正方形边长为1,连接小正方形的三个顶点,可得,则边上的高为______.
(3)如图4,在中,是边上的高,,,,设,求的值.
参考答案
1.解:A.,且,,故是直角三角形;
B.,且,,,,故不是直角三角形;
C.,,故是直角三角形;
D.,可设,,,,,故是直角三角形.
故选B.
2.解:第一个图形:两个小正方形的面积分别为4和9,大正方形的面积为13,可得,可得,可以验证勾股定理.
第二个图形:梯形的面积,化简得;可以证明勾股定理.
第三个图形:中间小正方形的面积;化简得,可以证明勾股定理.
第四个图形:由图形可知割补前后的两个小直角三角形全等,则正方形的面积两个直角三角形的面积的和,即,化简得;可以证明勾股定理,
能够验证勾股定理的有4个.
故选:A.
3.解:如图所示,根据赵爽弦图,将小正方形分成4个全等的直角三角形,和一个最小的正方形,
设直角三角形的短直角边长为,长直角边为,则正方形的水平宽度与垂直高度为,
依题意,
解得:
∴小正方形的边长为:,
故选:A.
4.解:由题意得,,
故选B.
5.解:∵,
∴点Р表示的数是.
故选D.
6.解:如图,在中,已知,所以,
所以他们仅仅少走了.
故选:
7.解:设绳索有x尺长,
则,
解得:.
故选:C.
8.解:如图,延长交于P,延长交于Q,
由题意得,,
∴,
∴,
∴,
同理可证,
∴,
∵图2是由图1放入长方形内得到,
∴,,
∴长方形的面积.
故选:B.
9.解:
解:如图,由勾股定理得
.
∵点C表示-1,
∴点A表示的数是.
故答案为:.
10.解:如图,
∵正方形a,c的边长分别为a和c,
∴,,
由正方形的性质得:,,
∵,,
∴,
在和中,,
∴,
∴,
∴,
∴正方形b的面积为,
即,
故答案为:.
11.解:如图,
过点作于点,
∵米,米,米,
∴米,
在中,由勾股定理得到:(米);
故答案是:米.
12.解:由题意:,,
正方形、、的面积依次为5、6、20,
,
.
故答案为:9.
13.解:根据题意,将圆柱展开如下:
∴,
∴,
∴最短路程为10,
故答案为:10.
14.解:∵,,即直角三角形的两直角边长为,
∴小正方形的边长为,
∴.
故答案为:
15.解:过点作交于点,交于点,
在正方形中,
又
∵正方形的面积为25,
或(舍去)
故答案为:
16.解:如图,作于点,则,
四边形、四边形、四边形都是正方形,
,,,
,
,
,,
,,,
,
,,
,
,,
,
,
,
,
,
,
,,
,
,
,
①,
,
②,
由①②得,
,
,
故答案为:36.
17.(1)解:如图,即为所求;(答案不唯一)
此时:;
(2)解:如图,即为所求;(答案不唯一)
此时:.
18.解:点C位置如图,
则 ,,
在直角 中, ,
答:彩色胶带的长至少是 .
19.(1)解:;
理由:∵,
∴,
∴,
∴,
即;
(2)解:连接,,
∵,
∴,,,
∴,
又∵
,
∴ ,
整理得: .
20.解:(1)在中,OB===,
∴,
∴点C表示的数是,
故答案为:;
(2)解:设秋千绳索AC的长度为,
由题意可得AC=AB=,
∵,
∴,
在中,,
∴,
解得,
即AC的长度为,
答:绳索AC的长为.
21.(1)证明:∵,,,
∴
∴
∴
(2),
,
,
即AB边上的高是
(3)解:在中,由勾股定理得
∵,
∴
在中,由勾股定理得
∴,
∴
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
