18.1.1平行四边形的性质学案
文档属性
| 名称 | 18.1.1平行四边形的性质学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 251.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-11 00:00:00 | ||
图片预览

文档简介
课题:平行四边形的性质
学习目标:
1. 了解平行四边形的定义,表示方法.
2. 通过画、猜、量、证理解平行四边形的对边、对角的性质.
3. 根据平行四边形的性质会进行简单的计算和证明;
学习重点: 平行四边形对角、对边的性质
学习难点: 利用平行四边形对边、对角的性质解决相关问题 ;
学习用具:练习本,刻度尺,量角器,圆规等工具
学习模式:先自主学习后同桌合作学习.
学习程序
一 自主学行四边形是随处可见的熟悉图形,
( http: / / www.21cnjy.com )
2 观察上图:两组对边分别 的四边形叫做平行四边形. 教室里你能找到平行四边形吗
几何语言表述 ∵ AB CD AD BC
∴四边形ABCD是平行四边形
平行四边形的表示:用图形 “ ”表示,
如:平行四边形ABCD记作;
二 合作学习 (同桌之间共同讨论完成)
在学习中,我们已经初步认识了平行四边形, ( http: / / www.21cnjy.com )知道平行四边形的两组对边分别平行,这是它的一个主要特征。除此之外,平行四边形还有什么特征呢?(同桌之间先讨论,讨论完成之后再完成下面提问)
1.请你根据平行四边形的定义在方框内画一个平行四边形。
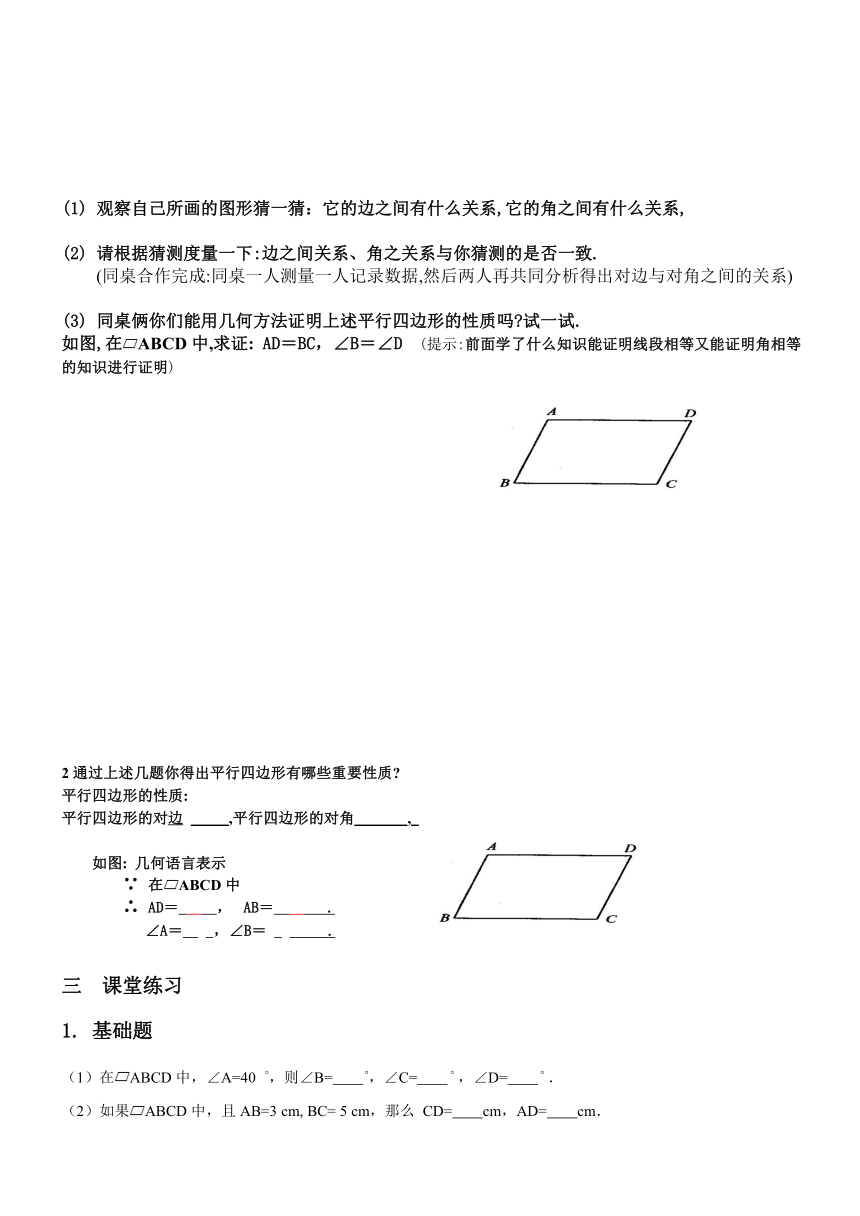
(1) 观察自己所画的图形猜一猜:它的边之间有什么关系,它的角之间有什么关系,
(2) 请根据猜测度量一下:边之间关系、角之关系与你猜测的是否一致.
(同桌合作完成:同桌一人测量一人记录数据,然后两人再共同分析得出对边与对角之间的关系)
(3) 同桌俩你们能用几何方法证明上述平行四边形的性质吗 试一试.
如图,在ABCD中,求证: AD=BC,∠B=∠D (提示:前面学了什么知识能证明线段相等又能证明角相等的知识进行证明)
2通过上述几题你得出平行四边形有哪些重要性质
平行四边形的性质:
平行四边形的对边 ,平行四边形的对角 ,
如图: 几何语言表示
∵ 在ABCD中
∴ AD= , AB= .
∠A= ,∠B= .
三 课堂练习
1. 基础题
(1)在ABCD中,∠A=40 ,则∠B= ,∠C= ,∠D= .
(2)如果ABCD中,且AB=3 cm, BC= 5 cm,那么 CD= cm,AD= cm.
2. 提高题
如下图是两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间的垂线段的长度。
( http: / / www.21cnjy.com )
经过度量,我们发现这些垂线段的长度都 .(从图中也可以看到这一点)。这种现象说明了平行线的又一个重要性质:
平行线之间的距离处处 。
应用
如图,如果直线l1∥l2,那么△ABC的面 ( http: / / www.21cnjy.com )积和△DBC的面积相等吗 。你能说出理由吗?你还能在两条平行线l1、l2之间画出其他与△ABC面积相等的三角形吗?画一两个试一试.
( http: / / www.21cnjy.com )
四 课堂小结
1、定义:两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:
平行四边形的对边 ,平行四边形的对角 ,
如图: 几何语言表示
∵ 在ABCD中
∴ AB// AD //
AD= , AB= .
∠A= ,∠B= .
3.两平行线的性质: 平行线之间的距离处处 。
五 课堂检测 (有困难的学生只要完成1,2,3题)
1.在ABCD中,∠A=120,则∠B= ,∠C= ,∠D= .
如果ABCD的周长为24cm,且AB =5,那
么BC= cm,CD= cm,AD= cm.
3.如图,□ABCD中,CE⊥AB,垂足为E,
如果∠A=115°,则∠BCE=______.
4.若在□ABCD中,∠A=30°,AB=7cm,AD=6cm,则S□ABCD=______.
5.在□ABCD中,周长等于48,
已知一边长12,求各边的长
已知AB=2BC,求各边的长
六 兴趣作业
1.□ABCD中,两邻角之比为1∶2,则它的四个内角的度数分别是____________.
2.□ABCD的周长是28cm,△ABC的周长是22cm,则AC的长是__________.
3.如图,在□ABCD中,M、N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由.它们的位置关系如何呢?
学习目标:
1. 了解平行四边形的定义,表示方法.
2. 通过画、猜、量、证理解平行四边形的对边、对角的性质.
3. 根据平行四边形的性质会进行简单的计算和证明;
学习重点: 平行四边形对角、对边的性质
学习难点: 利用平行四边形对边、对角的性质解决相关问题 ;
学习用具:练习本,刻度尺,量角器,圆规等工具
学习模式:先自主学习后同桌合作学习.
学习程序
一 自主学行四边形是随处可见的熟悉图形,
( http: / / www.21cnjy.com )
2 观察上图:两组对边分别 的四边形叫做平行四边形. 教室里你能找到平行四边形吗
几何语言表述 ∵ AB CD AD BC
∴四边形ABCD是平行四边形
平行四边形的表示:用图形 “ ”表示,
如:平行四边形ABCD记作;
二 合作学习 (同桌之间共同讨论完成)
在学习中,我们已经初步认识了平行四边形, ( http: / / www.21cnjy.com )知道平行四边形的两组对边分别平行,这是它的一个主要特征。除此之外,平行四边形还有什么特征呢?(同桌之间先讨论,讨论完成之后再完成下面提问)
1.请你根据平行四边形的定义在方框内画一个平行四边形。
(1) 观察自己所画的图形猜一猜:它的边之间有什么关系,它的角之间有什么关系,
(2) 请根据猜测度量一下:边之间关系、角之关系与你猜测的是否一致.
(同桌合作完成:同桌一人测量一人记录数据,然后两人再共同分析得出对边与对角之间的关系)
(3) 同桌俩你们能用几何方法证明上述平行四边形的性质吗 试一试.
如图,在ABCD中,求证: AD=BC,∠B=∠D (提示:前面学了什么知识能证明线段相等又能证明角相等的知识进行证明)
2通过上述几题你得出平行四边形有哪些重要性质
平行四边形的性质:
平行四边形的对边 ,平行四边形的对角 ,
如图: 几何语言表示
∵ 在ABCD中
∴ AD= , AB= .
∠A= ,∠B= .
三 课堂练习
1. 基础题
(1)在ABCD中,∠A=40 ,则∠B= ,∠C= ,∠D= .
(2)如果ABCD中,且AB=3 cm, BC= 5 cm,那么 CD= cm,AD= cm.
2. 提高题
如下图是两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间的垂线段的长度。
( http: / / www.21cnjy.com )
经过度量,我们发现这些垂线段的长度都 .(从图中也可以看到这一点)。这种现象说明了平行线的又一个重要性质:
平行线之间的距离处处 。
应用
如图,如果直线l1∥l2,那么△ABC的面 ( http: / / www.21cnjy.com )积和△DBC的面积相等吗 。你能说出理由吗?你还能在两条平行线l1、l2之间画出其他与△ABC面积相等的三角形吗?画一两个试一试.
( http: / / www.21cnjy.com )
四 课堂小结
1、定义:两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:
平行四边形的对边 ,平行四边形的对角 ,
如图: 几何语言表示
∵ 在ABCD中
∴ AB// AD //
AD= , AB= .
∠A= ,∠B= .
3.两平行线的性质: 平行线之间的距离处处 。
五 课堂检测 (有困难的学生只要完成1,2,3题)
1.在ABCD中,∠A=120,则∠B= ,∠C= ,∠D= .
如果ABCD的周长为24cm,且AB =5,那
么BC= cm,CD= cm,AD= cm.
3.如图,□ABCD中,CE⊥AB,垂足为E,
如果∠A=115°,则∠BCE=______.
4.若在□ABCD中,∠A=30°,AB=7cm,AD=6cm,则S□ABCD=______.
5.在□ABCD中,周长等于48,
已知一边长12,求各边的长
已知AB=2BC,求各边的长
六 兴趣作业
1.□ABCD中,两邻角之比为1∶2,则它的四个内角的度数分别是____________.
2.□ABCD的周长是28cm,△ABC的周长是22cm,则AC的长是__________.
3.如图,在□ABCD中,M、N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由.它们的位置关系如何呢?
