2015连线中考数学一轮复习系列专题17多边形与平行四边形
文档属性
| 名称 | 2015连线中考数学一轮复习系列专题17多边形与平行四边形 |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 17:43:48 | ||
图片预览




文档简介
基础知识
知识点一:四边形
四边形
内角和:360°
外角和:360°
多边形
内角和公式:
外角和等于360°
知识点二:平面图形的密铺:
1、定义:用 形状、 大小 完全相同的一种或几种平面图形进行拼接,彼此之间 不留空隙 、不重叠 地铺成一起,这就是平面图形的密铺,又称作平面图形的 镶嵌 。
2、密铺的方法:⑴用同一种正多边形密铺,可以用正三角形、正四边形或正六边形。
⑵用两种正多边形密铺,组合方式
有: 正三角形 和正四边形 、正三角形 和正六边形、 正四边形 和 正八边形 等几种。
知识点三:平行四边形
定义:两组对边分别平行的四边形称为平行四边形
平行四边形的性质
平行四边形的判定
重点例题分析
例1:七边形外角和为( )
A.180° B.360° C.900° D.1260°
例2:一个多边形的内角和是900°,这个多边形的边数是( )
A.4 B.5 C.6 D.7
例3:四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.OA=OC,OB=OD B.AD∥BC,AB∥DC C.AB=DC,AD=BC D.AB∥DC,AD=BC
∴四边形ABCD是平行四边形.故能能判定这个四边形是平行四边形;
D、AB∥DC,AD=BC,
∴四边形ABCD是平行四边形或等腰梯形.故不能能判定这个四边形是平行四边形.
故选D.
例4:如图19-1,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
A.13 B.14 C.15 D.16
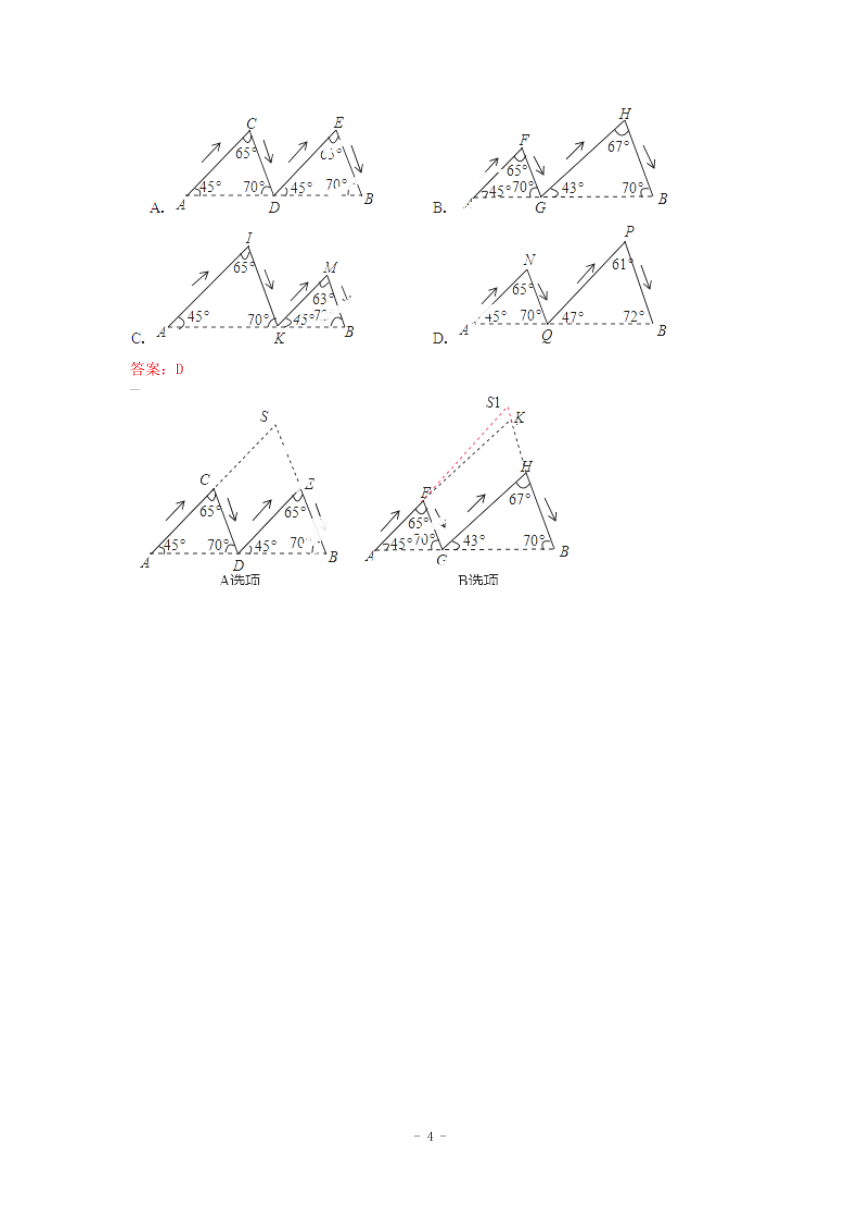
例5:在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )
答案:D
同理可证得AI+IK+KM+MB<AS2+BS2<AN+NQ+QP+PB,又∵AS+BS<AS2+BS2,故选D.
例6:如图19-2,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
求证:BE=DF;(2)求证:AF∥CE.
答案:证明:(1)∵四边形ABCD是平行四边形,
例7:如图19-3,在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造 PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
(1)当点C运动到线段OB的中点时,求t的值及点E的坐标.
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形.
(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在一,四象限,在运动过程中 PCOD的面积为S.
①当点M,N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;
②若点M,N中恰好只有一个点落在四边形ADEC的内部(不包括边界)时,直接写出S的取值范围.
∵MF∥PD,
∴EMF∽△EDP,
巩固练习
下列说法中,正确的是( )
同位角相等 B.对角线相等的四边形是平行四边形
C.四条边相等的四边形是菱形 D.矩形的对角线一定互相垂直
2.如图19-4,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB//DC,AD//BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB//DC,AD=BC
3.如图19-5,在平行四边形ABCD中,下列结论中错误的是( ),
∠1=∠2 B.∠BAD=∠BCD C.AB=CD D.AC⊥BD
如图19-6,在 ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )
A.1:2 B.1:3 C.1:4 D.1:5
5.若一个多边形外角和与内角和相等,则这个多边形是 边形.
6.已知一个多边形的内角和是1080°,这个多边形的边数是 .
7.已知如图19-7,菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值为 .
8.如图19-8,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
9.如图19-9,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
10.如图19-10,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求出此时DM的值.
中考预测
1.用下列一种多边形不能铺满地面的是( )
A.正方形 B.正十边形 C.正六边形 D.等边三角形
2.已知 ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D. 60°
3.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6 C.5或7 D.5或6或7
4.将一个n边形变成n+1边形,内角和将( )
A.减少180° B.增加90° C.增加180° D.增加360°
四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD;从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
6.如图19-11,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )
A.3:4 B.:2 C.:2 D.2:
7.正十二边形每个内角的度数为 150°
.
如图, ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为 .
9.如图19-12,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
10.如图19-13,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
11.如图19-14,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC. 设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1) 求证:OE=OF
(2)若CE=12,CF=5,求OC的长;
(3) 当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
12.如图19-15,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
答案:
巩固练习
C
D
D
A
7.5
8.证明:∵BE∥DF,
(2)设AP=x,则PD=4﹣x,
中考预测
6.D
7.150°
图19-8
PAGE
- 1 -
知识点一:四边形
四边形
内角和:360°
外角和:360°
多边形
内角和公式:
外角和等于360°
知识点二:平面图形的密铺:
1、定义:用 形状、 大小 完全相同的一种或几种平面图形进行拼接,彼此之间 不留空隙 、不重叠 地铺成一起,这就是平面图形的密铺,又称作平面图形的 镶嵌 。
2、密铺的方法:⑴用同一种正多边形密铺,可以用正三角形、正四边形或正六边形。
⑵用两种正多边形密铺,组合方式
有: 正三角形 和正四边形 、正三角形 和正六边形、 正四边形 和 正八边形 等几种。
知识点三:平行四边形
定义:两组对边分别平行的四边形称为平行四边形
平行四边形的性质
平行四边形的判定
重点例题分析
例1:七边形外角和为( )
A.180° B.360° C.900° D.1260°
例2:一个多边形的内角和是900°,这个多边形的边数是( )
A.4 B.5 C.6 D.7
例3:四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.OA=OC,OB=OD B.AD∥BC,AB∥DC C.AB=DC,AD=BC D.AB∥DC,AD=BC
∴四边形ABCD是平行四边形.故能能判定这个四边形是平行四边形;
D、AB∥DC,AD=BC,
∴四边形ABCD是平行四边形或等腰梯形.故不能能判定这个四边形是平行四边形.
故选D.
例4:如图19-1,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
A.13 B.14 C.15 D.16
例5:在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )
答案:D
同理可证得AI+IK+KM+MB<AS2+BS2<AN+NQ+QP+PB,又∵AS+BS<AS2+BS2,故选D.
例6:如图19-2,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
求证:BE=DF;(2)求证:AF∥CE.
答案:证明:(1)∵四边形ABCD是平行四边形,
例7:如图19-3,在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造 PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
(1)当点C运动到线段OB的中点时,求t的值及点E的坐标.
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形.
(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在一,四象限,在运动过程中 PCOD的面积为S.
①当点M,N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;
②若点M,N中恰好只有一个点落在四边形ADEC的内部(不包括边界)时,直接写出S的取值范围.
∵MF∥PD,
∴EMF∽△EDP,
巩固练习
下列说法中,正确的是( )
同位角相等 B.对角线相等的四边形是平行四边形
C.四条边相等的四边形是菱形 D.矩形的对角线一定互相垂直
2.如图19-4,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB//DC,AD//BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB//DC,AD=BC
3.如图19-5,在平行四边形ABCD中,下列结论中错误的是( ),
∠1=∠2 B.∠BAD=∠BCD C.AB=CD D.AC⊥BD
如图19-6,在 ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )
A.1:2 B.1:3 C.1:4 D.1:5
5.若一个多边形外角和与内角和相等,则这个多边形是 边形.
6.已知一个多边形的内角和是1080°,这个多边形的边数是 .
7.已知如图19-7,菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值为 .
8.如图19-8,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
9.如图19-9,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
10.如图19-10,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求出此时DM的值.
中考预测
1.用下列一种多边形不能铺满地面的是( )
A.正方形 B.正十边形 C.正六边形 D.等边三角形
2.已知 ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D. 60°
3.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6 C.5或7 D.5或6或7
4.将一个n边形变成n+1边形,内角和将( )
A.减少180° B.增加90° C.增加180° D.增加360°
四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD;从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
6.如图19-11,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )
A.3:4 B.:2 C.:2 D.2:
7.正十二边形每个内角的度数为 150°
.
如图, ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为 .
9.如图19-12,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
10.如图19-13,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
11.如图19-14,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC. 设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1) 求证:OE=OF
(2)若CE=12,CF=5,求OC的长;
(3) 当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
12.如图19-15,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
答案:
巩固练习
C
D
D
A
7.5
8.证明:∵BE∥DF,
(2)设AP=x,则PD=4﹣x,
中考预测
6.D
7.150°
图19-8
PAGE
- 1 -
同课章节目录
