2015连线中考数学一轮复习系列专题18特殊的平行四边
文档属性
| 名称 | 2015连线中考数学一轮复习系列专题18特殊的平行四边 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 17:43:14 | ||
图片预览



文档简介
基础知识
知识点一:矩形
定义:有一个角是直角的平行四边形叫做矩形。
矩形的判定
矩形的性质
知识点二:菱形
定义:四边都相等的四边形是菱形或有一组邻边相等的平行四边形是菱形
菱形的判定
菱形的性质
知识点三:正方形
定义:有一组邻边相等且一个角是直角的平行四边形叫做正方形。
正方形的判定
正方形的性质
重点例题分析
例1:下列命题是真命题的是( )
A.四边形都相等的四边形是矩形 B.菱形的对角线相等
C.对角线互相垂直的平行四边形是正方形 D.对角线相等的梯形是等腰梯形
答案:D
例2:正方形的一条对角线长为4,则这个正方形的面积是( )
A. B. C. D.
例3:如图20-1,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A. B. C. D.
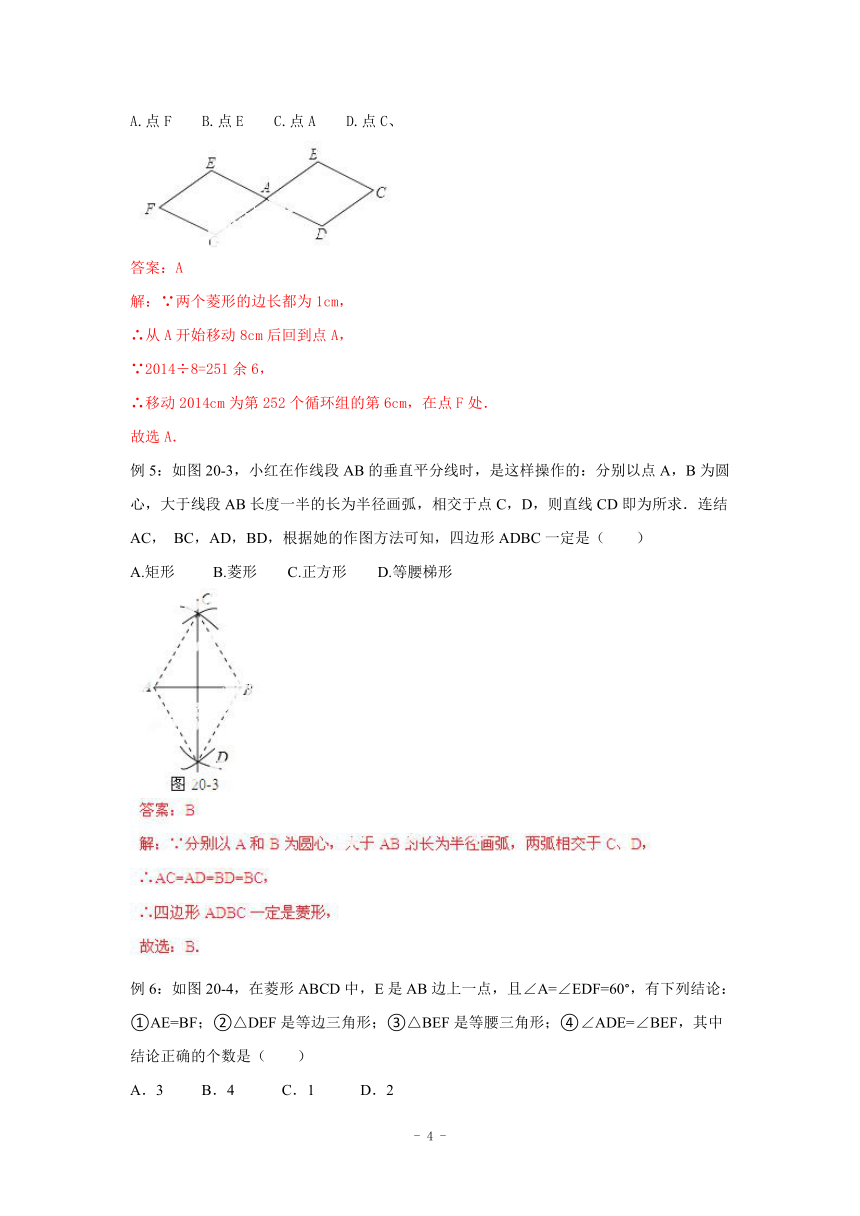
例4:如图20-2,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )
A.点F B.点E C.点A D.点C、
答案:A
解:∵两个菱形的边长都为1cm,
∴从A开始移动8cm后回到点A,
∵2014÷8=251余6,
∴移动2014cm为第252个循环组的第6cm,在点F处.
故选A.
例5:如图20-3,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连结AC, BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
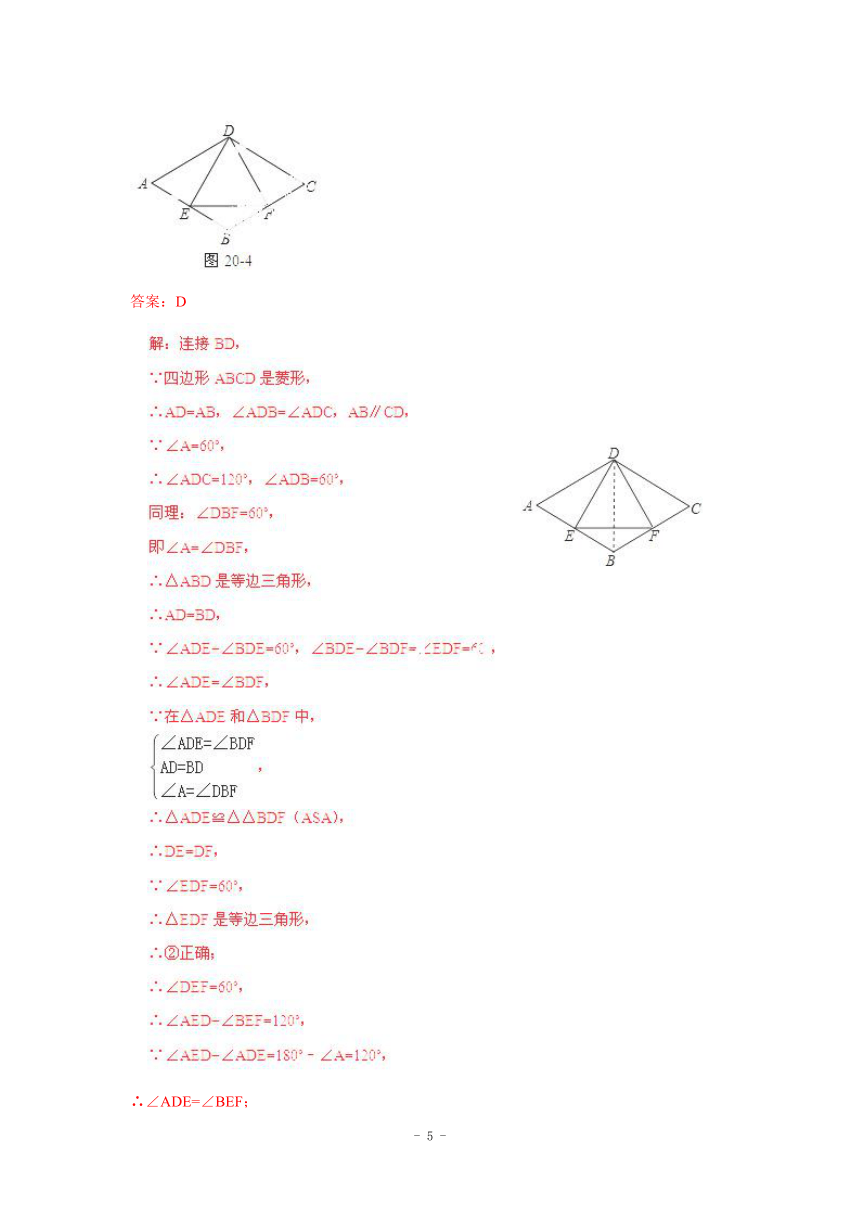
例6:如图20-4,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3 B.4 C. 1 D.2
答案:D
∴∠ADE=∠BEF;
故④正确.
∵∠ADE=∠BDF,
同理:∠BDE=∠CDF,
但∠ADE不一定等于∠BDE,
∴AE不一定等于BE,
故①错误;
∵△ADE≌△△BDF,
∴AE=BF,
同理:BE=CF,
但BE不一定等于BF.
故③错误.
故选D.
例7:如图20-5,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )
A.4 B. C. D.5
∴菱形ABCD的面积是×AC DB=×6×8=24
∴BC AE=24,
AE=,
故选:C.
例8:如图20-6,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 .
例9:如图20-7,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为 .
例10:在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
(1)如图1,当点G在BC边上时,易证:PG=PC.(不必证明)
(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,写出你的猜想(不必证明).
∴CH=CG,∠DCH=∠BCG,
巩固练习
1.如图20-8,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连结AB、AD、CD,则四边形ABCD一定是( )
A.平行四边形 B.矩形 C.菱形 D.梯形
2.如图20-9,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是( )
A.△AED≌△BFA B.DE-BF=EF
C.△BGF∽△DAE D.DE-BG=FG
3.如图20-10,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )
A. 3 B.3. 5 C.2.5 D.2.8
4.如图20-11,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园(围墙最长可利用),现在已备足可以砌长的墙的材料,试设计一种砌法,使矩形花园的面积为.
5.如图20-12,矩形ABCD对角线相交与O,DE//AC,CE//BD.求证:四边形OCED是菱形.
6.如图20-13,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=50° ,求∠BAO的大小.
7.如图20-14,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.
8.如图20-15,已知平行四边形ABCD,过A作AM⊥BC与M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.
(1)求证:四边形AECF为平行四边形;
(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值。
9.如图20-16,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
(1)求证:四边形BCEF是平行四边形;
(2)若∠ABC=900,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形。
中考预测
下列命题中正确的是( )
对角线相等的四边形是矩形 B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
2.如图20-17,在菱形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OC
3.正方形ABCD在直角坐标系中的位置如图20-18表示,将正方形ABCD绕点A顺时针方向旋转180°后,C点的坐标是( )
A.(2,0) B. (3,0) C. (2,﹣1) D. (2,1)
4.如图20-19,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的周长为 .
5.如图20-20,CD与BE互相垂直平分,AD⊥DB,∠BDE=700,则∠CAD= 0.
6.如图20-21,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为 .
7.如图20-22所示,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BF⊥a于点F、DE⊥a于点E,若DE=8,BF=5,则EF的长为 .
8.如图20-23,以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是__ ___.
9.已知在平面直角坐标系中放置了5个如图20-24所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3,以此继续下去,则点A2014到x轴的距离是 .
10.如图20-25,△ABC中,,AB=6cm,BC=8cm。将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连结AD。求证:四边形ACFD是菱形。
11.已知:如图20-26,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2。
(1)若CE=1,求BC的长;(2)求证AM=DF+ME。
图20-5
图20-7
图20-23
PAGE
- 16 -
知识点一:矩形
定义:有一个角是直角的平行四边形叫做矩形。
矩形的判定
矩形的性质
知识点二:菱形
定义:四边都相等的四边形是菱形或有一组邻边相等的平行四边形是菱形
菱形的判定
菱形的性质
知识点三:正方形
定义:有一组邻边相等且一个角是直角的平行四边形叫做正方形。
正方形的判定
正方形的性质
重点例题分析
例1:下列命题是真命题的是( )
A.四边形都相等的四边形是矩形 B.菱形的对角线相等
C.对角线互相垂直的平行四边形是正方形 D.对角线相等的梯形是等腰梯形
答案:D
例2:正方形的一条对角线长为4,则这个正方形的面积是( )
A. B. C. D.
例3:如图20-1,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A. B. C. D.
例4:如图20-2,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )
A.点F B.点E C.点A D.点C、
答案:A
解:∵两个菱形的边长都为1cm,
∴从A开始移动8cm后回到点A,
∵2014÷8=251余6,
∴移动2014cm为第252个循环组的第6cm,在点F处.
故选A.
例5:如图20-3,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连结AC, BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
例6:如图20-4,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3 B.4 C. 1 D.2
答案:D
∴∠ADE=∠BEF;
故④正确.
∵∠ADE=∠BDF,
同理:∠BDE=∠CDF,
但∠ADE不一定等于∠BDE,
∴AE不一定等于BE,
故①错误;
∵△ADE≌△△BDF,
∴AE=BF,
同理:BE=CF,
但BE不一定等于BF.
故③错误.
故选D.
例7:如图20-5,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )
A.4 B. C. D.5
∴菱形ABCD的面积是×AC DB=×6×8=24
∴BC AE=24,
AE=,
故选:C.
例8:如图20-6,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 .
例9:如图20-7,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为 .
例10:在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
(1)如图1,当点G在BC边上时,易证:PG=PC.(不必证明)
(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,写出你的猜想(不必证明).
∴CH=CG,∠DCH=∠BCG,
巩固练习
1.如图20-8,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连结AB、AD、CD,则四边形ABCD一定是( )
A.平行四边形 B.矩形 C.菱形 D.梯形
2.如图20-9,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是( )
A.△AED≌△BFA B.DE-BF=EF
C.△BGF∽△DAE D.DE-BG=FG
3.如图20-10,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )
A. 3 B.3. 5 C.2.5 D.2.8
4.如图20-11,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园(围墙最长可利用),现在已备足可以砌长的墙的材料,试设计一种砌法,使矩形花园的面积为.
5.如图20-12,矩形ABCD对角线相交与O,DE//AC,CE//BD.求证:四边形OCED是菱形.
6.如图20-13,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=50° ,求∠BAO的大小.
7.如图20-14,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.
8.如图20-15,已知平行四边形ABCD,过A作AM⊥BC与M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.
(1)求证:四边形AECF为平行四边形;
(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值。
9.如图20-16,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
(1)求证:四边形BCEF是平行四边形;
(2)若∠ABC=900,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形。
中考预测
下列命题中正确的是( )
对角线相等的四边形是矩形 B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
2.如图20-17,在菱形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OC
3.正方形ABCD在直角坐标系中的位置如图20-18表示,将正方形ABCD绕点A顺时针方向旋转180°后,C点的坐标是( )
A.(2,0) B. (3,0) C. (2,﹣1) D. (2,1)
4.如图20-19,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的周长为 .
5.如图20-20,CD与BE互相垂直平分,AD⊥DB,∠BDE=700,则∠CAD= 0.
6.如图20-21,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为 .
7.如图20-22所示,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BF⊥a于点F、DE⊥a于点E,若DE=8,BF=5,则EF的长为 .
8.如图20-23,以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是__ ___.
9.已知在平面直角坐标系中放置了5个如图20-24所示的正方形(用阴影表示),点B1在y轴上且坐标是(0,2),点C1、E1、E2、C2、E3、E4、C3在x轴上,C1的坐标是(1,0).B1C1∥B2C2∥B3C3,以此继续下去,则点A2014到x轴的距离是 .
10.如图20-25,△ABC中,,AB=6cm,BC=8cm。将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连结AD。求证:四边形ACFD是菱形。
11.已知:如图20-26,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2。
(1)若CE=1,求BC的长;(2)求证AM=DF+ME。
图20-5
图20-7
图20-23
PAGE
- 16 -
同课章节目录
