期中考试(新疆维吾尔自治区伊犁哈萨克自治州奎屯市)
文档属性
| 名称 | 期中考试(新疆维吾尔自治区伊犁哈萨克自治州奎屯市) |  | |
| 格式 | rar | ||
| 文件大小 | 135.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-02 15:18:00 | ||
图片预览



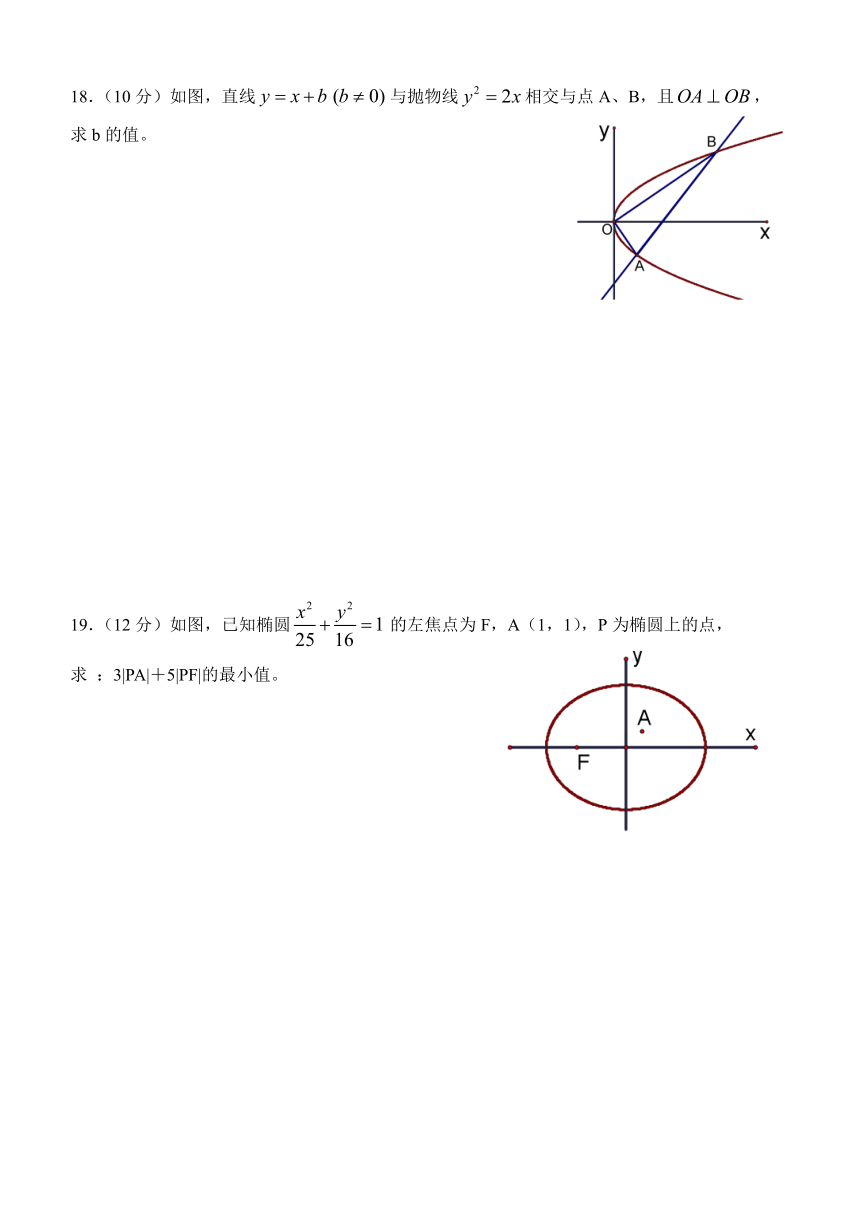
文档简介
奎屯市第一高级中学高二第二次月考
数学卷
一、选择题(请把答案填入后面的括号里。)
1.过点M(0,1)和N(的直线的倾斜角的是: ( )
A. B. C. D.
2.若直线在x轴上的截距为1,则m等于: ( )
A.1 B.2 C. D.2或
3.已知直线的图像如图所示,则: ( )
A.若 B.若
C.若 D.若
4.直线为: ( )
A. B. C. D.
5.的三个顶点A(4,1),B(-1,-6),C(-3,2),R为这个三角形三边围成的区域(包括边界),当P(x,y)在R中变动时,S=4x-3y的最大及最小值为: ( )
A.14和-18 B.18和-14 C.13和-18 D.14和-13
6.抛物线的焦点坐标是: ( )
A. B. C. D.
7.若椭圆的离心率,则等于: ( )
A. B. C. D.
8.焦点在y轴上,焦距是16,离心率是的双曲线方程是: ( )
A. B. C. D.
9.已知双曲线的渐近线方程为,则此双曲线的: ( )
A.焦距为10 B.实轴与虚轴分别为8和6 C.离心率是 D.离心率不确定
10.过抛物线的焦点F作倾斜角是的直线,交抛物线于A、B两点,则|AB|等于: ( )
A.8 B. C. D.16
11.曲线与直线有两个公共点时,实数k的取值范围是: ( )
A. B. C. D.
12.已知椭圆与双曲线有相同的焦点(-c,0)和(c,0),若c是a与m的等比中项,是与的等差中项,则椭圆的离心率为:( )
A. B. C. D.
奎屯市第一高级中学第二次月考(数学卷)
答题卷
一、选择题答题表
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题:
13.已知点,则经过点M(1,1)且以向量为方向的直线的方程为: 。
14.已知双曲线的渐近线为,且过点。则双曲线标准方程: 。
15.若方程表示椭圆,则m的取值范围是: 。
16.在中,B ( -2 , 0)、C ( 2 , 0)、A(x , y),给出满足的条件,就能得到动点A的轨迹方程,请你把下面的条件和其对应的方程连起来:(错一条不得分)
周长为 ……① Ⅰ:
面积为 ……② Ⅱ:
中, …③ Ⅲ :
三、解答题
17.(10分)已知直线与点A(3,3)和B(5,2)的距离相等,且过两直线
的交点,求直线的方程。
18.(10分)如图,直线与抛物线相交与点A、B,且,
求b的值。
19.(12分)如图,已知椭圆的左焦点为F,A(1,1),P为椭圆上的点,
求 :3|PA|+5|PF|的最小值。
20.(12分)若直线与双曲线的右支交于不同两点A、B,求实数k的取值范围。
21.(12分) 设椭圆的左焦点为(-2,0),左准线与x轴交于点N(-3,0),过点N且倾斜角为的直线交椭圆与A、B两点。
(文、理科)求直线与椭圆的方程;
(理科)求证:点(-2,0)在以线段AB为直径的圆上。
22.(14分)如图所示,已知A、B为椭圆与双曲线的公共顶点。P、Q分别为双曲线和椭圆上不同于A、B的动点,且有,设AP、BP、AQ、BQ的斜率分别为,求证:
奎屯市第一高级中学第二次月考答案
一、选择题:
1
2
3
4
5
6
7
8
9
10
11
12
B
D
D
C
A
D
C
B
C
D
B
A
二、填空题:
13: ;14: ;15: ;
16:①——Ⅲ ②——Ⅰ ③——Ⅱ
三、解答题:
17、解:由解得交点P为(1,2),根据题意,所求直线为过P点与AB平行或过P点与A、B中点Q()。
即
即
18、解:设交点,由可得
解方程组 整理得
即
19、解:因为F为椭圆左焦点,
作椭圆的左准线
由椭圆第二定义可得 ,得
如图,由,当三点共线时取最小值。
20、解:将代入,消y得 …………①
原问题等价于方程①有两个正根,即:
21、解:(Ⅰ)由题可得,直线方程为:
(或 或 )
由已知椭圆中c=2, 可得:
椭圆的方程为:
(Ⅱ)解方程组:
……①
②代入①,整理得:
……②
设
解法一:
所以点在以AB为直径的圆上。
解法二:
所以点在以AB为直径的圆上。
22、证明:设点P,Q的坐标分别为,由于点P在双曲线上,Q在椭圆上,则
数学卷
一、选择题(请把答案填入后面的括号里。)
1.过点M(0,1)和N(的直线的倾斜角的是: ( )
A. B. C. D.
2.若直线在x轴上的截距为1,则m等于: ( )
A.1 B.2 C. D.2或
3.已知直线的图像如图所示,则: ( )
A.若 B.若
C.若 D.若
4.直线为: ( )
A. B. C. D.
5.的三个顶点A(4,1),B(-1,-6),C(-3,2),R为这个三角形三边围成的区域(包括边界),当P(x,y)在R中变动时,S=4x-3y的最大及最小值为: ( )
A.14和-18 B.18和-14 C.13和-18 D.14和-13
6.抛物线的焦点坐标是: ( )
A. B. C. D.
7.若椭圆的离心率,则等于: ( )
A. B. C. D.
8.焦点在y轴上,焦距是16,离心率是的双曲线方程是: ( )
A. B. C. D.
9.已知双曲线的渐近线方程为,则此双曲线的: ( )
A.焦距为10 B.实轴与虚轴分别为8和6 C.离心率是 D.离心率不确定
10.过抛物线的焦点F作倾斜角是的直线,交抛物线于A、B两点,则|AB|等于: ( )
A.8 B. C. D.16
11.曲线与直线有两个公共点时,实数k的取值范围是: ( )
A. B. C. D.
12.已知椭圆与双曲线有相同的焦点(-c,0)和(c,0),若c是a与m的等比中项,是与的等差中项,则椭圆的离心率为:( )
A. B. C. D.
奎屯市第一高级中学第二次月考(数学卷)
答题卷
一、选择题答题表
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题:
13.已知点,则经过点M(1,1)且以向量为方向的直线的方程为: 。
14.已知双曲线的渐近线为,且过点。则双曲线标准方程: 。
15.若方程表示椭圆,则m的取值范围是: 。
16.在中,B ( -2 , 0)、C ( 2 , 0)、A(x , y),给出满足的条件,就能得到动点A的轨迹方程,请你把下面的条件和其对应的方程连起来:(错一条不得分)
周长为 ……① Ⅰ:
面积为 ……② Ⅱ:
中, …③ Ⅲ :
三、解答题
17.(10分)已知直线与点A(3,3)和B(5,2)的距离相等,且过两直线
的交点,求直线的方程。
18.(10分)如图,直线与抛物线相交与点A、B,且,
求b的值。
19.(12分)如图,已知椭圆的左焦点为F,A(1,1),P为椭圆上的点,
求 :3|PA|+5|PF|的最小值。
20.(12分)若直线与双曲线的右支交于不同两点A、B,求实数k的取值范围。
21.(12分) 设椭圆的左焦点为(-2,0),左准线与x轴交于点N(-3,0),过点N且倾斜角为的直线交椭圆与A、B两点。
(文、理科)求直线与椭圆的方程;
(理科)求证:点(-2,0)在以线段AB为直径的圆上。
22.(14分)如图所示,已知A、B为椭圆与双曲线的公共顶点。P、Q分别为双曲线和椭圆上不同于A、B的动点,且有,设AP、BP、AQ、BQ的斜率分别为,求证:
奎屯市第一高级中学第二次月考答案
一、选择题:
1
2
3
4
5
6
7
8
9
10
11
12
B
D
D
C
A
D
C
B
C
D
B
A
二、填空题:
13: ;14: ;15: ;
16:①——Ⅲ ②——Ⅰ ③——Ⅱ
三、解答题:
17、解:由解得交点P为(1,2),根据题意,所求直线为过P点与AB平行或过P点与A、B中点Q()。
即
即
18、解:设交点,由可得
解方程组 整理得
即
19、解:因为F为椭圆左焦点,
作椭圆的左准线
由椭圆第二定义可得 ,得
如图,由,当三点共线时取最小值。
20、解:将代入,消y得 …………①
原问题等价于方程①有两个正根,即:
21、解:(Ⅰ)由题可得,直线方程为:
(或 或 )
由已知椭圆中c=2, 可得:
椭圆的方程为:
(Ⅱ)解方程组:
……①
②代入①,整理得:
……②
设
解法一:
所以点在以AB为直径的圆上。
解法二:
所以点在以AB为直径的圆上。
22、证明:设点P,Q的坐标分别为,由于点P在双曲线上,Q在椭圆上,则
