2015连线中考数学一轮复习系列专题2-整式
文档属性
| 名称 | 2015连线中考数学一轮复习系列专题2-整式 |  | |
| 格式 | zip | ||
| 文件大小 | 529.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 17:44:17 | ||
图片预览




文档简介
第二讲 整式
基础知识
知识点一、代数式及求代数式的值
1. 用运算符号把数及表示数的字母连接起来的式子叫做代数式,单独的一个数或字母也是代数式。
2. 求代数式的值的步骤:(1)代入;(2)计算.有的时候常常构造出一个整体,再代入计算.
知识点二、整式的有关概念
1. 单项式:数或字母的积,这样 ( http: / / www.21cnjy.com )的式子是单项式.特别的,单独的一个数或字母也是单项式.单项式中的数字因数叫做这个单项式的系数,所有字母的指数和是这个单项式的次数.
2. 多项式:几个单项式的和是多项 ( http: / / www.21cnjy.com )式.多项式中所含单项式的个数就是项数;多项式里次数最高的项的次数,就是这个多项式的次数.多项式中不含字母的项是常数项.
3. 整式:单项式和多项式统称整式.
知识点三、同类项及合并同类项
1. 同类项: 所含字母相同,并且 ( http: / / www.21cnjy.com )相同字母的指数也分别相同的项是同类项.识别是否是同类项的时候要注意两相同:⑴具有相同的字母,⑵相同字母的指数相同;两无关:⑴与单项式的系数无关,⑵与字母的顺序无关
2. 把多项式中的同类项合并成一项,即把它们的系数相加作为新的系数,而字母部分不变,叫做合并同类项.
知识点四、整式的加减
1. 去括号法则
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变符号;
括号前是“一”号,把括号和它前面的“一”号去掉,括号里各项都改变符号.
2. 添括号法则
添上“+”号和括号,括到括 ( http: / / www.21cnjy.com )号里的各项都不变号;添上“一”号和括号,括到括号里的各项都改变符号.注意添上“-”号和括号,括到括号里的各项都改变符号.
3. 整式的加减
整式加减的实质就是去括号,合并同类项。
知识点四、幂的运算
1. 同底数幂的乘法 (都是正整数);
2. 幂的乘方 (m,n都是正整数);
3. 积的乘方法则 (n是正整数)
4. 同底数幂的除法法则 都是正整数,并且
知识点五、整式的乘法
1. 单项式与单项式相乘的法则
单项式与单项式相乘,就是把它们的系数、相同字母分别相乘,对于只在一个单项式中含有的字母,则连同它的指数作为积的一个因式.
2. 单项式与多项式相乘的乘法法则
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
m(a+b+c)=ma+mb+mc
3. 多项式相乘的乘法法则
多项式与多项式相乘,先用一个多项式的每 ( http: / / www.21cnjy.com )一项去乘另一个多项式的每一项,再把所得的积相加. (a+b)(c+d)= ac+ad+bc+bd
知识点六.整式的除法
1. 单项式相除的除法法则
单项式相除,把系数与同底数幂分别相除作为商的一个因式,对于只在被除数里含有的字母,则连同它的指数作为商的一个因式.
2. 多项式除以单项式的法则
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
用字母表示为
知识点七、乘法公式
1.平方差公式:
2. 完全平方公式:
知识点八、因式分解
1. 因式分解的定义
把一个多项式化成几个整式的积的形式的变形叫做把这个多项式因式分解,也叫把这个多项式分解因式.
2. 因式分解的方法
①提公因式法ma+mb+mc = m(a+b+c)
②公式法
(1)平方差公式法:a2-b2=(a+b)(a-b)
(2)完全平方公式:a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2
3. 因式分解步骤
1. 首先考虑提公因式法
2. 运用公式法
3. 检查分解的彻底性,使每一个因式都不能在分解为止.
典型例题解析
例1. (泰安)下列运算中,正确的是( )
A. B. C. D.
( http: / / www.21cnjy.com )
例2. (荆州)若-2xm-ny2与3x4y2m+n是同类项,则m-3n的立方根是 .
( http: / / www.21cnjy.com )
例3. (湘西州)已知x-2y=3,则代数式6-2x+4y的值为( )
A.0 B.-1 C.-3 D.3
( http: / / www.21cnjy.com )
例4. (攀枝花)因式分解a2b-b的正确结果是( )
A.b(a+1)(a-1) B.a(b+1)(b-1) C.b(a2-1) D.b(a-1)2
答案:A.
例5. 现有边长为a的A类正方形卡片和边长为b的B类正方形卡片,及长为a,宽为b的C类长方形卡片各若干张,如果要拼成一个长为(a+2b)、宽为(2a+b)的大长方形,需要A类卡片 张,B类卡片 张,C类卡片 张.
( http: / / www.21cnjy.com )
例6 (乌鲁木齐)实数x满足x2-2x-1=0,求代数式(2x-1)2-x(x+4)+(x-2)(x+2)的值.
( http: / / www.21cnjy.com )
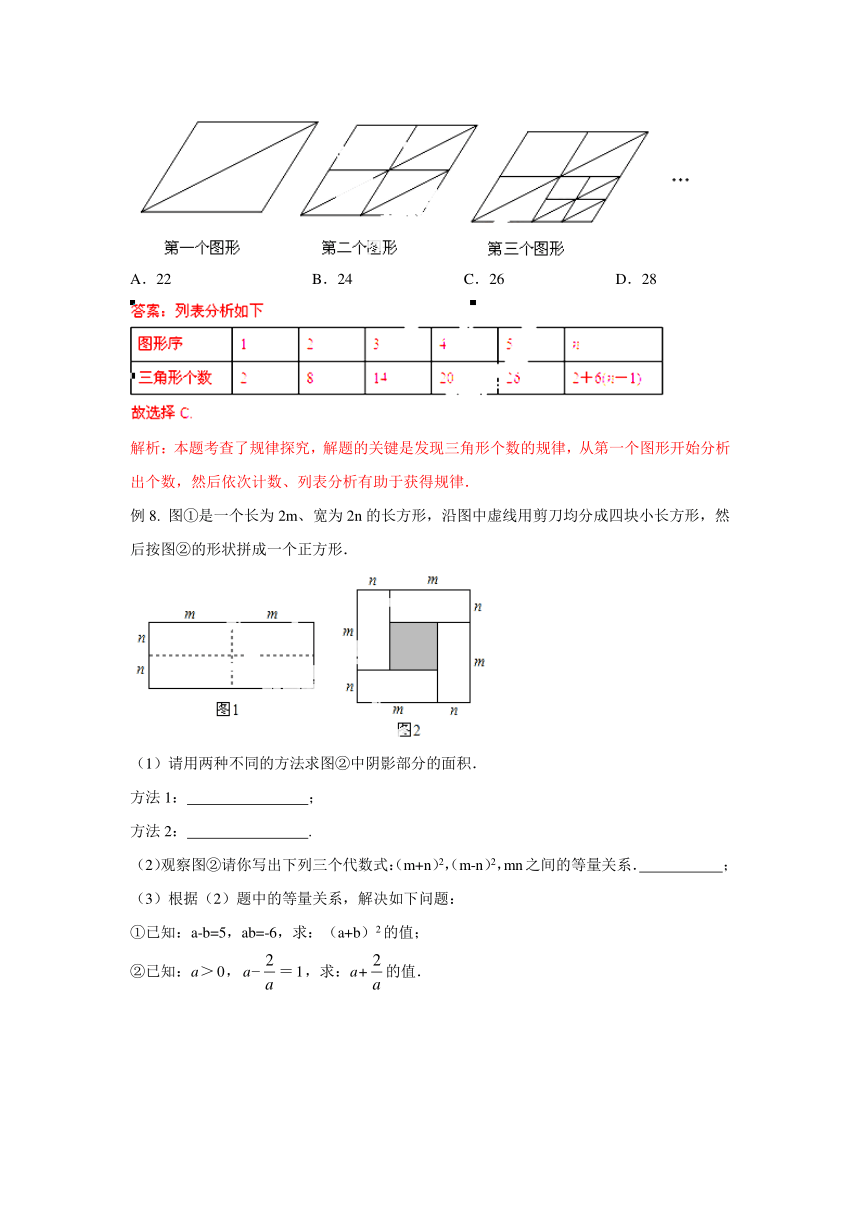
例7. (重庆)下列图形都是按照一 ( http: / / www.21cnjy.com )定规律组成,第一个图形中共有2个三角形,第二个图形中共有8个三角形,第三个图形中共有14个三角形,…,依此规律,第五个图形中三角形的个数是( )
( http: / / www.21cnjy.com )
A.22 B.24 C.26 D.28
解析:本题考查了规律探究,解题的关键是发现三角形个数的规律,从第一个图形开始分析出个数,然后依次计数、列表分析有助于获得规律.
例8. 图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
( http: / / www.21cnjy.com )
(1)请用两种不同的方法求图②中阴影部分的面积.
方法1: ;
方法2: .
(2)观察图②请你写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系. ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a-b=5,ab=-6,求:(a+b)2的值;
②已知:a>0,a =1,求:a+的值.
( http: / / www.21cnjy.com )
巩固训练
1. (镇江)下列运算正确的是( )
A.(x3)3=x9 B.(-2x)3=-6x3 C.2x2-x=x D.x6÷x3=x2
2. (湖南)已知x-2y=3,则代数式6-2x+4y的值为( )
A.0 B.﹣1 C.﹣3 D.3
3. (玉林)下面的多项式在实数范围内能因式分解的是( )
A.x2 + y B.x2 - y C.x2 + x + 1 D.x2 - 2x + 1
4. (镇江)化简:(x+1)(x-1)+1=_______.
5. (莱芜)因式分解:a3-4ab2= .
6. 在数轴上有示a、b、c三个实数的点的位置如图所示化简式子:|b-a|+|c-a|-|c-b|= .
7.(南昌)如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
( http: / / www.21cnjy.com )
A.2a-3b B.4a-8b C.2a-4b D.4a-10b
8. (武汉) 观察下列一组图形中点的个数,其中第一个图形中共有4个点,第2个图形中共有10个点,第3个图形中共有19个点,…
( http: / / www.21cnjy.com )
按此规律第5个图形中共有点的个数是( )
A.31 B.46 C.51 D.66
9. 张师傅下岗再就业,做起了小商品生意,第一次进货时,他以每件a元的价格购进了20件甲种小商品,每件b元的价格购进了30件乙种小商品(a>b);回来后,根据市场行情,他将这两种小商品都以每件 元的价格出售,在这次买卖中,张师傅赚 元钱
10. (百色)观察下列等式: ,…由以上规律可以得出第个等式为 .
11. (绍兴)先化简,再求值:a(a-3b)+(a+b)2-a(a-b),其中a=1,b=-.
12. (大庆)已知非零实数a满足,求的值.
中考预测
1. 计算的结果是( )
A.a5 B.﹣a5 C.a6 D.﹣a6
2. 下列运算正确的是( )
A. B.
C. D.
3. 将下列多项式分解因式,结果中不含因式的是( )
A. B. C. D.
4. 如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a-b)等于( )
A.7 B.6 C.5 D.4
( http: / / www.21cnjy.com )
5. 已知x(x+3)=1,则代数式2x2+6x-5的值为 .
6. 已知,,则= .
7. 一个大正方形和四个全等的小正方形按图① ( http: / / www.21cnjy.com )、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是 (用a,b的代数式表示).
( http: / / www.21cnjy.com )
8.如图,按此规律,第6行最后一个数字是 ,第 行最后一个数是2014.
( http: / / www.21cnjy.com )
9. 先化简,再求值:,其中x=-2.
10.观察下列关于自然数的等式:
32-4×12=5 ①
52-4×22=9 ②
72-4×32=13 ③
… …
根据上述规律解决下列问题:
(1)完成第四个等式:92-4×( )2=( );
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
11. 己知实数a、b满足 a+b =5,ab =3,求 a-b 的值
12. 如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形,
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a、b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.
(3)运用你所得到的公式,计算下列各题:
① 10.3×9.7 ②(2m+n-p)(2m-n+p)
( http: / / www.21cnjy.com )
3、D:解析:本题考查了多项式的因式分解,因式分解的方法有:(1)提公因式;(2)运
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
中考预测
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
基础知识
知识点一、代数式及求代数式的值
1. 用运算符号把数及表示数的字母连接起来的式子叫做代数式,单独的一个数或字母也是代数式。
2. 求代数式的值的步骤:(1)代入;(2)计算.有的时候常常构造出一个整体,再代入计算.
知识点二、整式的有关概念
1. 单项式:数或字母的积,这样 ( http: / / www.21cnjy.com )的式子是单项式.特别的,单独的一个数或字母也是单项式.单项式中的数字因数叫做这个单项式的系数,所有字母的指数和是这个单项式的次数.
2. 多项式:几个单项式的和是多项 ( http: / / www.21cnjy.com )式.多项式中所含单项式的个数就是项数;多项式里次数最高的项的次数,就是这个多项式的次数.多项式中不含字母的项是常数项.
3. 整式:单项式和多项式统称整式.
知识点三、同类项及合并同类项
1. 同类项: 所含字母相同,并且 ( http: / / www.21cnjy.com )相同字母的指数也分别相同的项是同类项.识别是否是同类项的时候要注意两相同:⑴具有相同的字母,⑵相同字母的指数相同;两无关:⑴与单项式的系数无关,⑵与字母的顺序无关
2. 把多项式中的同类项合并成一项,即把它们的系数相加作为新的系数,而字母部分不变,叫做合并同类项.
知识点四、整式的加减
1. 去括号法则
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变符号;
括号前是“一”号,把括号和它前面的“一”号去掉,括号里各项都改变符号.
2. 添括号法则
添上“+”号和括号,括到括 ( http: / / www.21cnjy.com )号里的各项都不变号;添上“一”号和括号,括到括号里的各项都改变符号.注意添上“-”号和括号,括到括号里的各项都改变符号.
3. 整式的加减
整式加减的实质就是去括号,合并同类项。
知识点四、幂的运算
1. 同底数幂的乘法 (都是正整数);
2. 幂的乘方 (m,n都是正整数);
3. 积的乘方法则 (n是正整数)
4. 同底数幂的除法法则 都是正整数,并且
知识点五、整式的乘法
1. 单项式与单项式相乘的法则
单项式与单项式相乘,就是把它们的系数、相同字母分别相乘,对于只在一个单项式中含有的字母,则连同它的指数作为积的一个因式.
2. 单项式与多项式相乘的乘法法则
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
m(a+b+c)=ma+mb+mc
3. 多项式相乘的乘法法则
多项式与多项式相乘,先用一个多项式的每 ( http: / / www.21cnjy.com )一项去乘另一个多项式的每一项,再把所得的积相加. (a+b)(c+d)= ac+ad+bc+bd
知识点六.整式的除法
1. 单项式相除的除法法则
单项式相除,把系数与同底数幂分别相除作为商的一个因式,对于只在被除数里含有的字母,则连同它的指数作为商的一个因式.
2. 多项式除以单项式的法则
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
用字母表示为
知识点七、乘法公式
1.平方差公式:
2. 完全平方公式:
知识点八、因式分解
1. 因式分解的定义
把一个多项式化成几个整式的积的形式的变形叫做把这个多项式因式分解,也叫把这个多项式分解因式.
2. 因式分解的方法
①提公因式法ma+mb+mc = m(a+b+c)
②公式法
(1)平方差公式法:a2-b2=(a+b)(a-b)
(2)完全平方公式:a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2
3. 因式分解步骤
1. 首先考虑提公因式法
2. 运用公式法
3. 检查分解的彻底性,使每一个因式都不能在分解为止.
典型例题解析
例1. (泰安)下列运算中,正确的是( )
A. B. C. D.
( http: / / www.21cnjy.com )
例2. (荆州)若-2xm-ny2与3x4y2m+n是同类项,则m-3n的立方根是 .
( http: / / www.21cnjy.com )
例3. (湘西州)已知x-2y=3,则代数式6-2x+4y的值为( )
A.0 B.-1 C.-3 D.3
( http: / / www.21cnjy.com )
例4. (攀枝花)因式分解a2b-b的正确结果是( )
A.b(a+1)(a-1) B.a(b+1)(b-1) C.b(a2-1) D.b(a-1)2
答案:A.
例5. 现有边长为a的A类正方形卡片和边长为b的B类正方形卡片,及长为a,宽为b的C类长方形卡片各若干张,如果要拼成一个长为(a+2b)、宽为(2a+b)的大长方形,需要A类卡片 张,B类卡片 张,C类卡片 张.
( http: / / www.21cnjy.com )
例6 (乌鲁木齐)实数x满足x2-2x-1=0,求代数式(2x-1)2-x(x+4)+(x-2)(x+2)的值.
( http: / / www.21cnjy.com )
例7. (重庆)下列图形都是按照一 ( http: / / www.21cnjy.com )定规律组成,第一个图形中共有2个三角形,第二个图形中共有8个三角形,第三个图形中共有14个三角形,…,依此规律,第五个图形中三角形的个数是( )
( http: / / www.21cnjy.com )
A.22 B.24 C.26 D.28
解析:本题考查了规律探究,解题的关键是发现三角形个数的规律,从第一个图形开始分析出个数,然后依次计数、列表分析有助于获得规律.
例8. 图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
( http: / / www.21cnjy.com )
(1)请用两种不同的方法求图②中阴影部分的面积.
方法1: ;
方法2: .
(2)观察图②请你写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系. ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a-b=5,ab=-6,求:(a+b)2的值;
②已知:a>0,a =1,求:a+的值.
( http: / / www.21cnjy.com )
巩固训练
1. (镇江)下列运算正确的是( )
A.(x3)3=x9 B.(-2x)3=-6x3 C.2x2-x=x D.x6÷x3=x2
2. (湖南)已知x-2y=3,则代数式6-2x+4y的值为( )
A.0 B.﹣1 C.﹣3 D.3
3. (玉林)下面的多项式在实数范围内能因式分解的是( )
A.x2 + y B.x2 - y C.x2 + x + 1 D.x2 - 2x + 1
4. (镇江)化简:(x+1)(x-1)+1=_______.
5. (莱芜)因式分解:a3-4ab2= .
6. 在数轴上有示a、b、c三个实数的点的位置如图所示化简式子:|b-a|+|c-a|-|c-b|= .
7.(南昌)如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
( http: / / www.21cnjy.com )
A.2a-3b B.4a-8b C.2a-4b D.4a-10b
8. (武汉) 观察下列一组图形中点的个数,其中第一个图形中共有4个点,第2个图形中共有10个点,第3个图形中共有19个点,…
( http: / / www.21cnjy.com )
按此规律第5个图形中共有点的个数是( )
A.31 B.46 C.51 D.66
9. 张师傅下岗再就业,做起了小商品生意,第一次进货时,他以每件a元的价格购进了20件甲种小商品,每件b元的价格购进了30件乙种小商品(a>b);回来后,根据市场行情,他将这两种小商品都以每件 元的价格出售,在这次买卖中,张师傅赚 元钱
10. (百色)观察下列等式: ,…由以上规律可以得出第个等式为 .
11. (绍兴)先化简,再求值:a(a-3b)+(a+b)2-a(a-b),其中a=1,b=-.
12. (大庆)已知非零实数a满足,求的值.
中考预测
1. 计算的结果是( )
A.a5 B.﹣a5 C.a6 D.﹣a6
2. 下列运算正确的是( )
A. B.
C. D.
3. 将下列多项式分解因式,结果中不含因式的是( )
A. B. C. D.
4. 如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a-b)等于( )
A.7 B.6 C.5 D.4
( http: / / www.21cnjy.com )
5. 已知x(x+3)=1,则代数式2x2+6x-5的值为 .
6. 已知,,则= .
7. 一个大正方形和四个全等的小正方形按图① ( http: / / www.21cnjy.com )、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是 (用a,b的代数式表示).
( http: / / www.21cnjy.com )
8.如图,按此规律,第6行最后一个数字是 ,第 行最后一个数是2014.
( http: / / www.21cnjy.com )
9. 先化简,再求值:,其中x=-2.
10.观察下列关于自然数的等式:
32-4×12=5 ①
52-4×22=9 ②
72-4×32=13 ③
… …
根据上述规律解决下列问题:
(1)完成第四个等式:92-4×( )2=( );
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
11. 己知实数a、b满足 a+b =5,ab =3,求 a-b 的值
12. 如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形,
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a、b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.
(3)运用你所得到的公式,计算下列各题:
① 10.3×9.7 ②(2m+n-p)(2m-n+p)
( http: / / www.21cnjy.com )
3、D:解析:本题考查了多项式的因式分解,因式分解的方法有:(1)提公因式;(2)运
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
中考预测
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
同课章节目录
