2015连线中考数学一轮复习系列专题19圆的基本性质
文档属性
| 名称 | 2015连线中考数学一轮复习系列专题19圆的基本性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 627.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-10 00:00:00 | ||
图片预览




文档简介
第十九讲 圆的基本性质
基础知识
知识点一、圆的有关概念
1. 圆的定义①(动态定义)在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点叫做圆心,线段OA叫做半径.以点O为圆心的圆记做“⊙O”.
②(静态定义)圆是到定点的距离等于定长的点的集合.即:圆上各点到圆心的距离都等于定长(半径),反之到圆心距离等于半径的点一定在圆上;
2.等圆:能够完全重合的圆叫等圆.同圆或等圆的半径相等.
3.确定圆的条件
确定一个圆有两个基本条件
①圆心(定点)——用来确定圆的位置;②半径(定长)——用来确定圆的大小.
经过不在同一直线上的三点确定一个圆.
知识点二、弦、弧、圆心角等相关概念
1. 弦与直径:
①弦:连接圆上任意两点的线段叫做弦,记做:弦AB,弦CD等.
②直径:经过圆心的弦叫做直径,直径等于半径的2倍.直径是圆中最长的弦.
2. 弧与半圆
①弧:圆上任意两点之间的部分叫做圆弧,简称弧,用符号“”表示,如以A、B为端点的弧记做,
②半圆:圆上任意一条直径的两个端点把圆分成两条弧,其中的每条弧都叫做半圆.
③劣弧、优弧:小于半圆的弧叫做劣弧,用弧上的两点表示;大于半圆的弧叫做优弧,用弧上三点表示.
④等弧:能够完全重合的弧叫等弧.
知识点三、弧、弦、圆心角之间的关系
1. 圆的旋转不变性
把圆绕着圆心旋转任意一个角度,都与原来的图形重合,我们把这种性质称为圆的旋转不变性.圆是中心对称图形,圆心是它的对称中心.
2. 弧、弦、圆心角之间的关系定理:
在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.圆心角的度数与它所对的弧的度数相等.
知识点四、垂径定理
1. 圆的轴对称性:
圆是轴对称图形,任何一条直径所在的直线都是它的对称轴.
2. 垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
如图,用符号语言叙述为:
∵ CD为⊙O的直径,CD⊥AB于点E
∴ AE=EB,,
3. 垂径定理基本图形的性质:
(1)有4对全等的直角三角形:Rt△CAD与Rt△CBD;Rt△CAM与Rt△CBM;Rt△OAM与Rt△OBM;Rt△MAD与Rt△MBD;特别在Rt△CAD与Rt△CBD中,直径CD是它们公共的斜边,AM、BM是CD上的高.
(2)有3个等腰三角形;△CAB、△OAB、△DAB.弦AB是它们的公共底边,直径CD是它们的顶角平分线和底边AB的垂直平分线.
(3)有3对弧相等:,,.
(4)添加辅助线的方法:连接半径或作垂直于弦的直径,是两种重要的添线方法.
知识点五.圆周角定理
1. 定义:
顶点在圆上,并且两边都与圆相交的角叫圆周角.
2. 圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半,同弧或等弧所对的圆周角相等,
3. 圆周角定理的推论
①半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
②圆内接四边形的对角互补.
典型例题解析
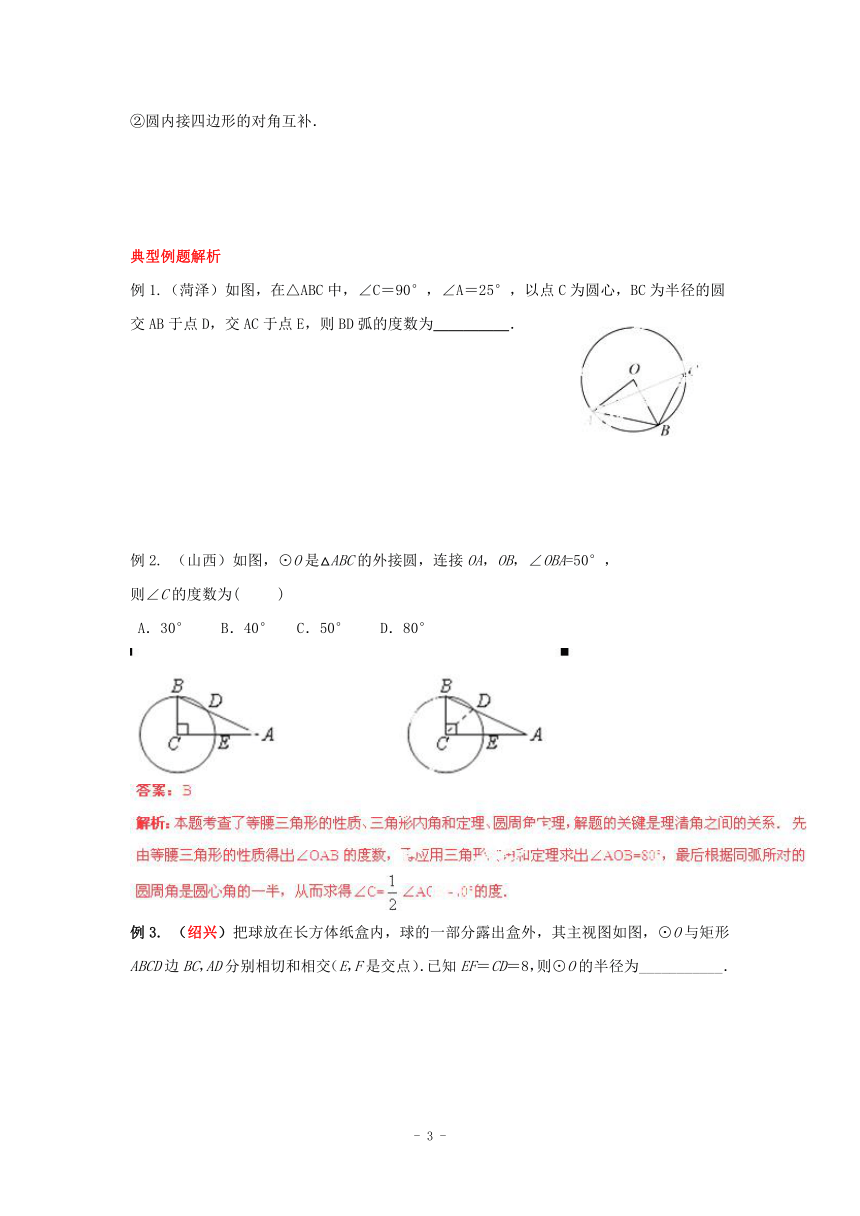
例1.(菏泽)如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则BD弧的度数为_____.
例2. (山西)如图,⊙O是△ABC的外接圆,连接OA,OB,∠OBA=50°,
则∠C的度数为( )
A.30° B.40° C.50° D.80°
例3. (绍兴)把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图,⊙O与矩形ABCD边BC,AD分别相切和相交(E,F是交点).已知EF=CD=8,则⊙O的半径为___________.
例4. (黑龙江)直径为10cm的⊙O中,弦AB=5cm,则弦AB所对的圆周角是 .
例5. (济南) 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
A. 2. B. C. D.
例6. (安徽)如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.
例7. 如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
巩固练习
1. (湖州)如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是( )
A. 35 ° B.45° C. 55° D.65°
2. 如图所示,在⊙O中,,那么( )
A.AB>2CD B.AB<2CD C.AB=2CD D.无法比较
3. (嘉兴)如图,○O的直径CD垂直弦AB于点E,且CE=2,DE=8则AB的长为( )
(A)2 (B)4 (C)6 (D)8
4. (钦州)如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )
A.60° B.45° C.30° D.20°
5. (南通)如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=_______度.
6. (广元)若⊙O的弦AB所对的圆心角∠AOB=50°,则弦AB所对的圆周角的度数为 .
7 . (龙岩) 如图,A、B、C是半径为6的⊙O上三个点,若∠BAC=45°,则弦BC= 。
8.(牡丹江)⊙O的半径为2,弦,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为 .
9. (南通)如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
10. 如图,已知△ABC中,以AB为直径的半⊙O交AC于D,交BC于E,BE=CE,∠C=70°,求∠DOE的度数.
11(邵阳)如图(八)所示,某窗户是由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高EF=1m,现计划安装玻璃,请帮工程师求出所在圆O的半径r.
12. (武汉) 如图,AB是⊙O的直径,C,P是 上两点,AB=13,AC=5.
(1)如图(1),若点P是 的中点,求PA的长;
(2)如图(2),若点P是 的中点,求PA的长;
中考预测
1. 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠BOC=( )
A. 25° B. 50° C. 130° D. 155°
2.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为( )
A.2 B.4 C.6 D.8
3. 如图,□ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是( )
A.44° B.54° C.72° D.53°
4. 如图,△ABC是⊙O的内接三角形,将△ABC绕圆心O逆时针方向旋转α°(0<α<90),得到△A′B′C′,若,则∠B的度数为( )
A.30° B.45° C.50° D.60°
5. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A.cm B.cm C. cm或cm D.cm或cm
6. 如图,在⊙O中,∠AOB的度数为m,C是弧ACB上一点,D、E是弧AB上不同的两点(不与A、B两点重合),则∠D+∠E的度数为 .(用含有m的代数式表示)
7. 如图,将半径为6的⊙O沿弦AB折叠,使经过圆心O,则弦AB= .
8. 如图是一个圆形人工湖的平面图,弦AB是湖上的一座桥,已知桥长100m,测得圆周角∠ACB=30°,则这个人工湖的直径为_________m.
9. 已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(I)如图,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(II)如图②,若∠CAB=60°,求BD的长.
10. 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
11.如图,等边△ABC内接于⊙O,P是弧AB上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)填空:∠APC= 度,∠BPC= 度;
(2)求证:△ACM≌△BCP;
12. 如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE.
(1)求∠ACB的度数;
(2)过点O作OF⊥AC于点F,延长FO交BE于点G,DE=3,EG=2,求AB的长.
PAGE
- 1 -
基础知识
知识点一、圆的有关概念
1. 圆的定义①(动态定义)在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点叫做圆心,线段OA叫做半径.以点O为圆心的圆记做“⊙O”.
②(静态定义)圆是到定点的距离等于定长的点的集合.即:圆上各点到圆心的距离都等于定长(半径),反之到圆心距离等于半径的点一定在圆上;
2.等圆:能够完全重合的圆叫等圆.同圆或等圆的半径相等.
3.确定圆的条件
确定一个圆有两个基本条件
①圆心(定点)——用来确定圆的位置;②半径(定长)——用来确定圆的大小.
经过不在同一直线上的三点确定一个圆.
知识点二、弦、弧、圆心角等相关概念
1. 弦与直径:
①弦:连接圆上任意两点的线段叫做弦,记做:弦AB,弦CD等.
②直径:经过圆心的弦叫做直径,直径等于半径的2倍.直径是圆中最长的弦.
2. 弧与半圆
①弧:圆上任意两点之间的部分叫做圆弧,简称弧,用符号“”表示,如以A、B为端点的弧记做,
②半圆:圆上任意一条直径的两个端点把圆分成两条弧,其中的每条弧都叫做半圆.
③劣弧、优弧:小于半圆的弧叫做劣弧,用弧上的两点表示;大于半圆的弧叫做优弧,用弧上三点表示.
④等弧:能够完全重合的弧叫等弧.
知识点三、弧、弦、圆心角之间的关系
1. 圆的旋转不变性
把圆绕着圆心旋转任意一个角度,都与原来的图形重合,我们把这种性质称为圆的旋转不变性.圆是中心对称图形,圆心是它的对称中心.
2. 弧、弦、圆心角之间的关系定理:
在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.圆心角的度数与它所对的弧的度数相等.
知识点四、垂径定理
1. 圆的轴对称性:
圆是轴对称图形,任何一条直径所在的直线都是它的对称轴.
2. 垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
如图,用符号语言叙述为:
∵ CD为⊙O的直径,CD⊥AB于点E
∴ AE=EB,,
3. 垂径定理基本图形的性质:
(1)有4对全等的直角三角形:Rt△CAD与Rt△CBD;Rt△CAM与Rt△CBM;Rt△OAM与Rt△OBM;Rt△MAD与Rt△MBD;特别在Rt△CAD与Rt△CBD中,直径CD是它们公共的斜边,AM、BM是CD上的高.
(2)有3个等腰三角形;△CAB、△OAB、△DAB.弦AB是它们的公共底边,直径CD是它们的顶角平分线和底边AB的垂直平分线.
(3)有3对弧相等:,,.
(4)添加辅助线的方法:连接半径或作垂直于弦的直径,是两种重要的添线方法.
知识点五.圆周角定理
1. 定义:
顶点在圆上,并且两边都与圆相交的角叫圆周角.
2. 圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半,同弧或等弧所对的圆周角相等,
3. 圆周角定理的推论
①半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
②圆内接四边形的对角互补.
典型例题解析
例1.(菏泽)如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则BD弧的度数为_____.
例2. (山西)如图,⊙O是△ABC的外接圆,连接OA,OB,∠OBA=50°,
则∠C的度数为( )
A.30° B.40° C.50° D.80°
例3. (绍兴)把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图,⊙O与矩形ABCD边BC,AD分别相切和相交(E,F是交点).已知EF=CD=8,则⊙O的半径为___________.
例4. (黑龙江)直径为10cm的⊙O中,弦AB=5cm,则弦AB所对的圆周角是 .
例5. (济南) 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
A. 2. B. C. D.
例6. (安徽)如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.
例7. 如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
巩固练习
1. (湖州)如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是( )
A. 35 ° B.45° C. 55° D.65°
2. 如图所示,在⊙O中,,那么( )
A.AB>2CD B.AB<2CD C.AB=2CD D.无法比较
3. (嘉兴)如图,○O的直径CD垂直弦AB于点E,且CE=2,DE=8则AB的长为( )
(A)2 (B)4 (C)6 (D)8
4. (钦州)如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )
A.60° B.45° C.30° D.20°
5. (南通)如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=_______度.
6. (广元)若⊙O的弦AB所对的圆心角∠AOB=50°,则弦AB所对的圆周角的度数为 .
7 . (龙岩) 如图,A、B、C是半径为6的⊙O上三个点,若∠BAC=45°,则弦BC= 。
8.(牡丹江)⊙O的半径为2,弦,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为 .
9. (南通)如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
10. 如图,已知△ABC中,以AB为直径的半⊙O交AC于D,交BC于E,BE=CE,∠C=70°,求∠DOE的度数.
11(邵阳)如图(八)所示,某窗户是由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高EF=1m,现计划安装玻璃,请帮工程师求出所在圆O的半径r.
12. (武汉) 如图,AB是⊙O的直径,C,P是 上两点,AB=13,AC=5.
(1)如图(1),若点P是 的中点,求PA的长;
(2)如图(2),若点P是 的中点,求PA的长;
中考预测
1. 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠BOC=( )
A. 25° B. 50° C. 130° D. 155°
2.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为( )
A.2 B.4 C.6 D.8
3. 如图,□ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是( )
A.44° B.54° C.72° D.53°
4. 如图,△ABC是⊙O的内接三角形,将△ABC绕圆心O逆时针方向旋转α°(0<α<90),得到△A′B′C′,若,则∠B的度数为( )
A.30° B.45° C.50° D.60°
5. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A.cm B.cm C. cm或cm D.cm或cm
6. 如图,在⊙O中,∠AOB的度数为m,C是弧ACB上一点,D、E是弧AB上不同的两点(不与A、B两点重合),则∠D+∠E的度数为 .(用含有m的代数式表示)
7. 如图,将半径为6的⊙O沿弦AB折叠,使经过圆心O,则弦AB= .
8. 如图是一个圆形人工湖的平面图,弦AB是湖上的一座桥,已知桥长100m,测得圆周角∠ACB=30°,则这个人工湖的直径为_________m.
9. 已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(I)如图,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(II)如图②,若∠CAB=60°,求BD的长.
10. 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
11.如图,等边△ABC内接于⊙O,P是弧AB上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)填空:∠APC= 度,∠BPC= 度;
(2)求证:△ACM≌△BCP;
12. 如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE.
(1)求∠ACB的度数;
(2)过点O作OF⊥AC于点F,延长FO交BE于点G,DE=3,EG=2,求AB的长.
PAGE
- 1 -
同课章节目录
